一种自适应交替的差分混合蛙跳优化算法

胥 枫，张桂珠，赵 芳，吴德龙

(江南大学物联网工程学院，江苏 无锡 214122)

1 概述

混合蛙跳算法(Shuffled Frog Leaping Algorithm，SFLA)是模拟青蛙觅食过程中群体信息共享和交流机制而产生的一种群智能算法，是一种全新的启发式群体智能进化算法。该算法由Eusuff 和Lansey 在2003 年首次提出，并成功解决了管道网络扩充中管道尺寸的最小化问题［1］。

混合蛙跳与其他群智能算法相比，具有概念简单、参数少、计算速度快、全局寻优能力强、易于实现等特点［2］，近年来已经被成功应用于多个领域。但混合蛙跳算法也存在着对初始值敏感、早熟收敛以及求解精度差等缺点［3］，为此许多学者对其进行改进，将该算法与其他群智能算法相结合以提高算法的性能，如与差分进化(Differential Evolution，DE)算法［4］、量子粒子群优化(Quantum-behaved Particle Swarm Optimization，OPSO)算 法［5］、模 拟 退 火(Simulated Annealing，SA)算法［6］等结合，都取得了不错的效果。混合蛙跳算法的性能改进已成为目前研究的热点问题。

粒子群优化(Particle Swarm Optimization，PSO)算法是1995 年由Kennedy 和Eberhart 提出的群智能算法［7］，是一种全局优化算法，能在较短的时间内求得高质量的解。文献［8］提出一种PSO 算法产生满足约束条件的初始解的方法，可用于各种算法初始解的产生。差分进化算法［9］最初由Store 和Price 于1995 年提出，该算法通过变异、杂交、选择操作来更新随机产生的初始种群，经过逐步迭代、不断进化，可实现全局最优解的搜索，具有较强的全局寻优能力，种群多样性好，但在算法的初期收敛速度较慢。

本文在借鉴前人研究成果的基础之上，提出一种自适应交替的差分混合蛙跳算法ADE-SFLA。将SFLA 算法与DE、PSO 这2 种算法相结合，利用PSO算法在短时间内生成一组高质量的初始解;并在搜索策略中，提出一种改进选择机制，交替使用SFLA和DE 这2 种算法，利用2 种算法搜索原理的不同，在算法轮替中相互扰动以丰富粒子多样性，并且继承了2 种算法各自的优势，使算法前期具有较快的收敛速度，后期进行更精确的局部搜索，以提高算法的性能。

2 混合蛙跳算法

2.1 初始化

随机生成N 只青蛙组成初始化群体F={X1，X2，…，Xn}，第k 只青蛙表示问题的解为Xk={xk1，xk2，…，xkl}，其中，l 表示变量的个数，即解空间的维数。

2.2 分组算子

将所有青蛙按照它们的初始适应度值进行降序排序，并分别放入各个模因组中。具体分组方法如下:将N 只青蛙青蛙按适应度值降序排列，并把种群分为m 个模因组，第1 只青蛙进入第1 个模因组，第2只青蛙进入第2 个模因组，……，第m 只青蛙进入第m 个模因组;然后第m+1 只青蛙进入到第1 个模因组，第m +2 只青蛙进入到第2 个模因组，直到所有青蛙分配完毕。在每个模因组中用Fb和Fw分别表示模因组中位置最好和最差的青蛙，用Fg表示整个种群中位置最好的青蛙。

2.3 局部位置更新算子

在模因组中的每一次进化过程中，对最差青蛙Fw位置进行调整，具体调整方法如下:

青蛙的移动距离为:

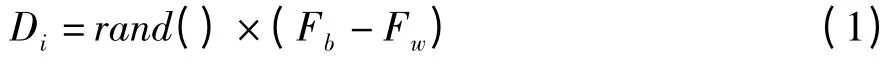
更新最差青蛙的位置:

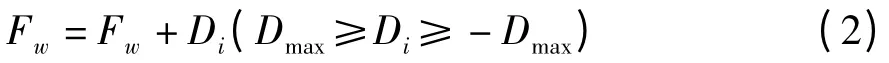
其中，rand()是0～1 之间的随机数;Dmax是允许青蛙移动的最大距离。

在位置调整过程中，如果最差青蛙经过上述过程能够产生一个较好的位置，就用新位置的青蛙取代原来位置的青蛙，即更新最差青蛙Fw;否则用Fg代替Fb。

重复上述过程，即用下式更新最差青蛙位置:

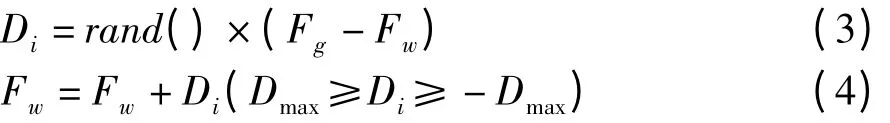
如果上述方法不能产生位置更好的青蛙或在调整过程中青蛙的移动距离超过了最大移动距离，那么就随机产生一个新解取代原来最差的青蛙Fw。按照这种方法，每个模因组内部经过一定次数的进化，对最差青蛙位置进行调整和更新。

2.4 全局更新算子

全局更新算子有助于收集各模因组内搜索的局部信息，通过模因组中信息在全局中的共享，获得新的搜索全局最优解的方向。当所有模因组经过组内最大迭代次数后，将各模因组中青蛙混合在一起，再将所有青蛙个体按适应度降序排列后，重新分组，这样使得青蛙个体的模因信息得到充分的传递，然后继续进行局部搜索，如此反复直至达到最大全局迭代次数或者满足收敛条件，算法停止。

3 改进的混合蛙跳算法

3.1 初始种群的产生

群智能算法都有一个普遍的特点:对初始值敏感，混合蛙跳算法也不例外。混合蛙跳算法的初始解是随机产生的，如果产生的随机解普遍适应度值不够理想，可能会影响算法的全局寻优性能，容易收敛到局部最优解。因此，必须对初始产生的青蛙种群进行优化。

理想的初始解应该有较好的适应度值，初始种群有较好的多样性。本文利用粒子群算法来产生初始解，粒子群算法的具体步骤见文献［10］。定义产生初始解的约束条件有3 个:粒子每维的分量落在指定的区间内，粒子的适应度值达到预定值，粒子的多样性达到规定要求。定义粒子群的初始群体L={X1，X2，…，Xk，…，Xn}，n 表示群体中粒子的个数，第k个粒子问题的解为Xk={xk1，xk2，…，xkl，…，xkd}，d 为解空间的维数。因此，本文提出初始解产生的数学算子为:

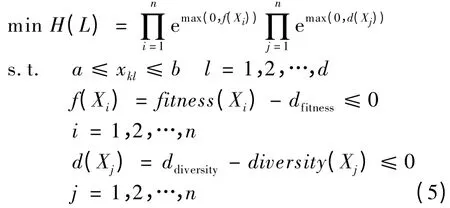
其中，a 和b 分别为搜索区间的下界与上界;fitness(X)是适应度函数;dfitness为适应度值阈值;ddiversity为多样性阈值;diversity(X)是多样性度量表达式中的xij表示第i个粒子的第j 维分量。

算法的基本思想:在给定区间范围内随机产生一组值作为粒子群算法的初始解，然后按照粒子群的粒子速度、位置更新公式更新粒子的速度和位置，每次计算H(L)时判断H(L)是否小于等于1，并且判断f(Xi)≤0，i=1，2，…，n 和d(Xj)≤0，j=1，2，…，n 是否都成立，若都成立，则记下该粒子的位置作为改进算法的一个初始解，并且重新在给定的区间范围内产生一新粒子以替换该粒子。重复上述过程，最终能找到满足约束条件的N 个位置作为改进算法的初始解。

3.2 改进的搜索策略

基于优势互补的思想，本文提出一种自适应交替的差分混合蛙跳算法。相对于差分进化算法，混合蛙跳算法在进化初期有较快的收敛速度，但在进化后期由于粒子的趋同性，导致粒子丧失多样性，易发生早熟收敛;相对于混合蛙跳算法，差分进化算法在进化初期的收敛速度较慢，但在进化的后期收敛速度较快，而且粒子多样性较好，为了结合两者的优势，需要一个合理的选择机制在搜索过程中交替使用这2 种算法。文献［4］提出了一种选择机制，类似于转盘机制:

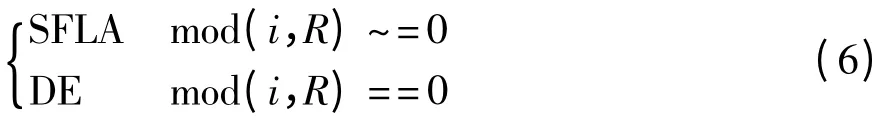
其中，i 是当前算法的迭代次数;R 是一个固定常数。在这种选择机制下，算法每进行R -1 次SFLA 全局迭代搜索后就进行一次DE 迭代搜索，相当于是给SFLA 搜索进行了一次DE 扰动，但是这种选择机制并没有真正结合SFLA 和DE 这2 种算法的优势，只是在原来SFLA 算法的基础上多了DE 扰动。为此，本文提出一种改进的选择机制:

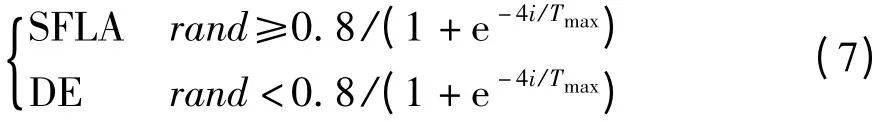
其中，i 是当前算法的迭代次数;rand 是0～1 之间的随机数;Tmax是算法最大迭代次数;0.8/(1 +e-4i/Tmax)是根据当前迭代次数产生0～1 的小数，前期产生数较小，后期产生的数较大。这个选择机制的作用:通过比较rand 和0.8/(1 +e-4i/Tmax)的大小，让算法前期以较大的概率进行SFLA 搜索，并以小概率随机地进行DE 扰动;后期以较大概率进行DE 搜索，并以小概率进行SFLA 扰动。这样不但能丰富粒子的多样性，而且继承了2 种算法在进化初期和后期的优秀性能，使算法在前期有较快的收敛速度，后期能够进行更精确的局部搜索。

改进算法ADE-SFLA 的步骤如下:

(1)初始化算法参数，包括种群的数量N，模因组数量M，组内迭代次数It，全局最大迭代次数Tmax等参数。

(2)用PSO 算法优化初始产生的种群，获得高质量的初始解。

(3)进行迭代过程:

4 实验仿真与结果分析

4.1 实验平台测试函数的介绍与参数的设置

为了检验改进算法的性能，设计实验环境在软件平台Matlab 上。

测试对象为6 个经典的连续函数，f1:Sphere 简单的单峰函数;f2:Rosenbrock 简单的多峰函数;f3:Rastrigin 复杂的多峰函数;f4:Griewank 复杂的多峰函数，f5:Ackely 复杂的多峰函数;f6:Schafferf7 复杂的多峰函数。

这些函数的理论全局最优解都为0。6 个函数表达式如下所示:

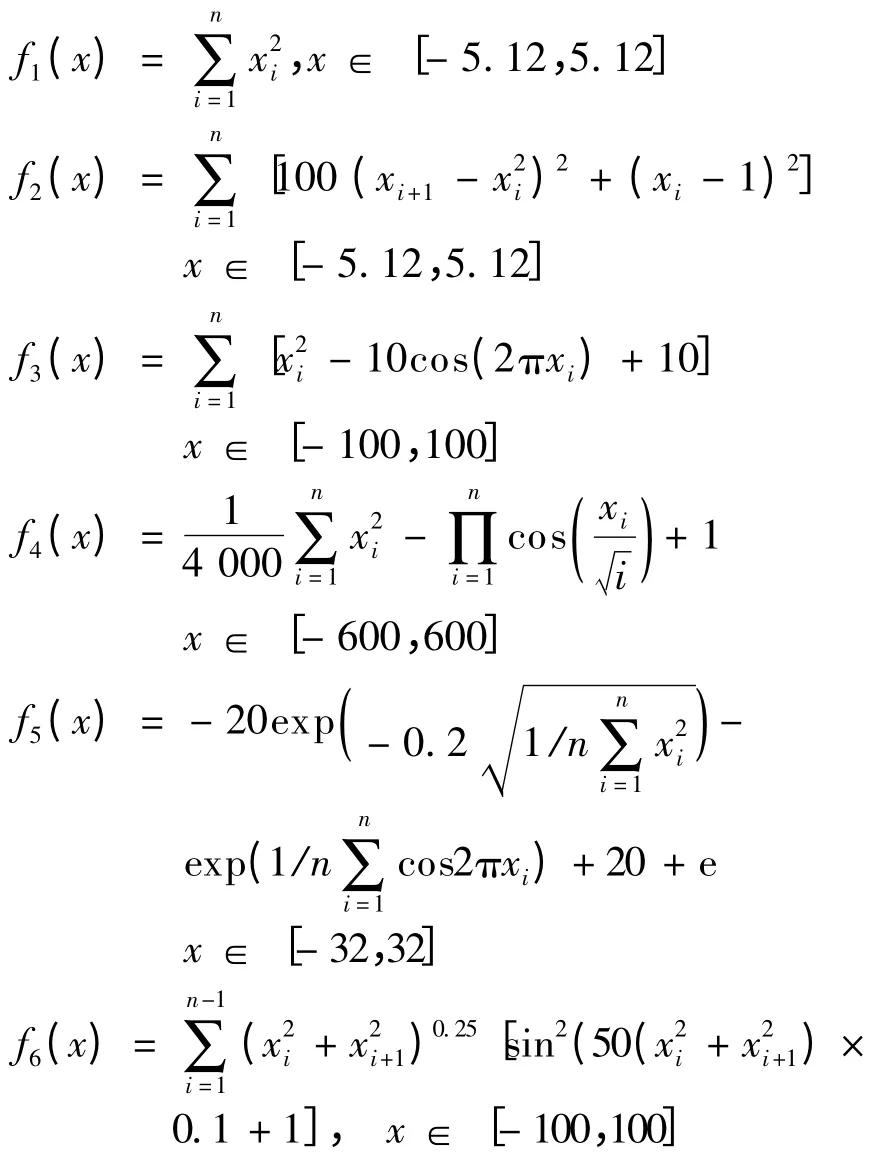
算法参数的设置:全局最大迭代次数为500 次，变量的维数n 为30。SFLA 算法的青蛙数量为200 个，模因组数为20 个，组内最大迭代次数为10 次［12］;DE 算法的缩放因子F 设置为0.5，交叉概率C 为0.3;PSO 算法的种群大小为20，惯性权重为0.9，认知权重c1和c2都设置为2.0，产生200 个初始解。将ADE-SFLA 算法与文献［4］改进的算法(简记为DE-SFLA)、SFLA、DE 算法进行对比实验。

4.2 实验结果分析

为了消除随机性对算法运行结果的影响，每个测试函数都分别独立运行30 次，4 种算法对6 个测试函数的实验结果如表1 所示。

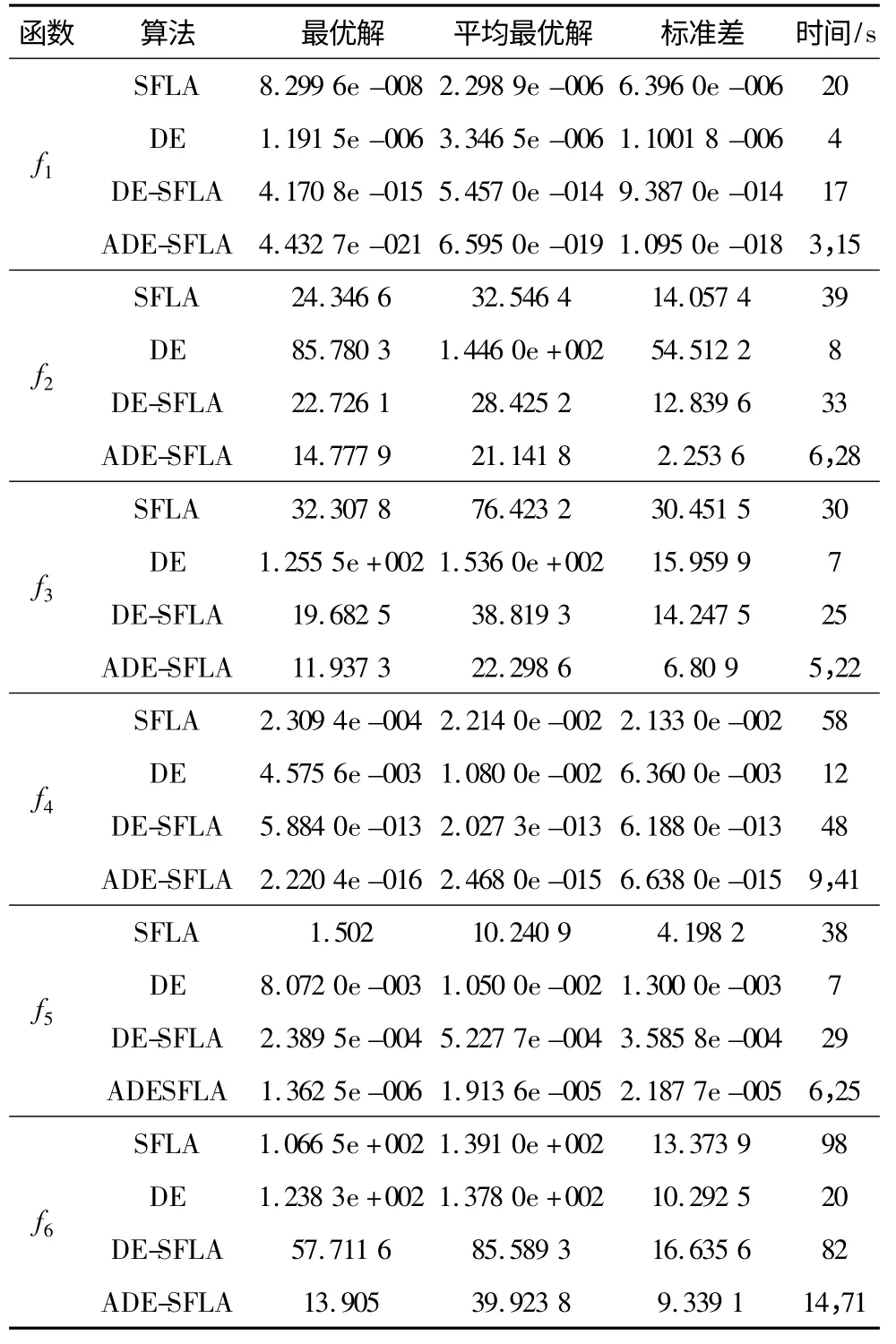
表1 固定迭代次数收敛的实验结果

表1 的数据显示，ADE-SFLA 的最优解、平均最优解都优于基本的SFLA 和DE，也优于赵鹏军等人的改进算法DE-SFLA，说明算法后期更够进行更精确的局部搜索，使得求解精度得到有效的提高，标准差也较小，表明ADE-SFLA 稳定性更好。在运行时间上，记录了ADE-SFLA 分别采用PSO 生成初始解的运行时间和算法全局迭代运行时间，虽然生成初始解花费了一点时间，但有了高质量的初始解，使ADE-SFLA 进入迭代后的速度明显快于DE-SFLA的速度。

图1～图6 为4 种算法分别对6 个函数搜索最优解的进化曲线。可见，ADE-SFLA 的初始解要优于DE-SFLA、SFLA 以及DE，普遍适应度值较优、多样性较好的初始解有利于算法的全局搜索，不易陷入局部极值。ADE-SFLA 的收敛速度及收敛精度也优于与之比较的3 个算法，表明本文提出的选择机制能够继承SFLA 和DE 各自的优势，算法前期有较快的寻优速度，后期使粒子保持良好的多样性，进行更精确的局部搜索，无论面对简单的单峰函数还是复杂的多峰函数都有较好的收敛性能。进一步论证了本文改进算法是可靠、有效的优化算法。

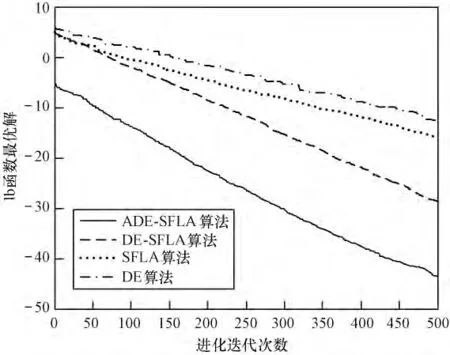
图1 各算法对Sphere 函数的寻优进化曲线

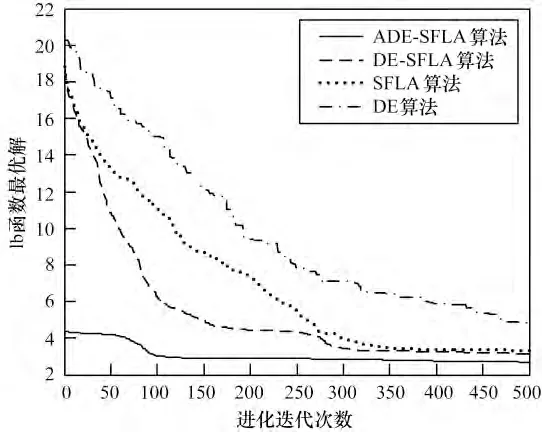
图2 各算法对Rosenbrock 函数的寻优进化曲线

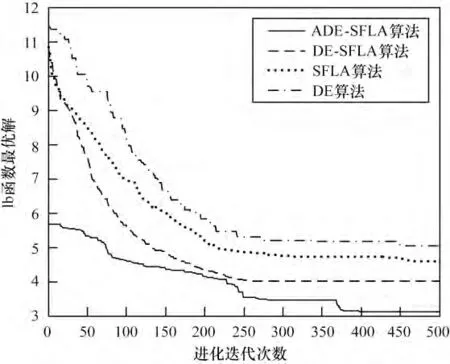
图3 各算法对Rastrigin 函数的寻优进化曲线

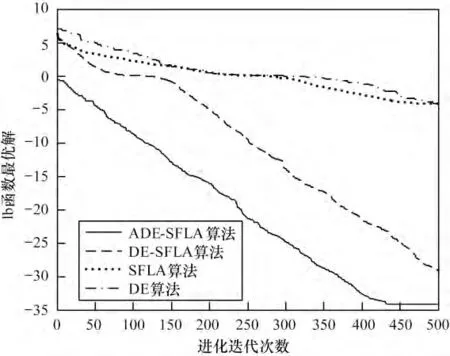
图4 各算法对Griewank 函数的寻优进化曲线

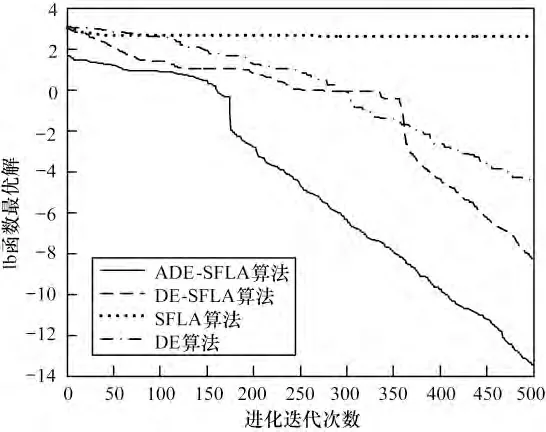
图5 各算法对Ackely 函数的寻优进化曲线

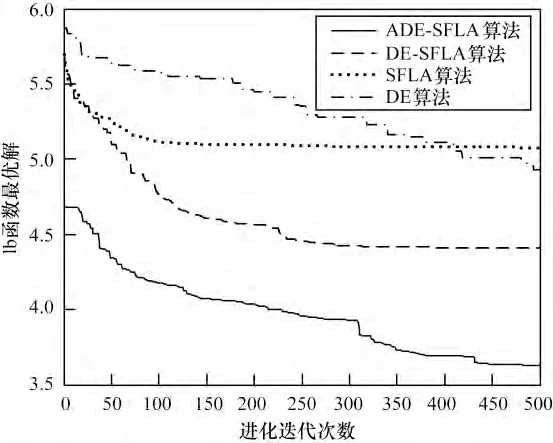
图6 各算法对Schafferf7 函数的寻优进化曲线

5 结束语

本文提出一种改进的混合蛙跳算法。该算法借鉴PSO 算法运行速度较快这一特点，在短时间内产生一组满足约束条件的初始解，以提高初始解的质量;根据SFLA 算法和DE 算法各自的特点，设计一个改进的选择机制，在搜索过程中自适应地轮替使用这2 种算法，有效地结合了2 种算法各自的优势。仿真实验结果表明，ADE-SFLA 算法无论是面对简单的单峰函数还是复杂的多峰函数都有较好的收敛性能，是一种可靠的全局优化算法。今后研究方向为:将该算法应用到软件测试当中，解决软件测试用例集的精简问题，以提高软件测试工作的效率。

［1］杨淑莹，张 桦.群体智能与仿生计算:Matlab 技术实现［M］.北京:电子工业出版社，2012.

［2］葛 宇，王学平，梁 静，等.自适应混沌变异蛙跳算法［J］.计算机应用研究，2011，28(3):945-947.

［3］赵鹏军，刘三阳.求解复杂函数优化问题的混合蛙跳算法［J］.计算机应用研究，2009，26(7):2435-2437.

［4］赵鹏军，邵泽军.一种新的改进的混合蛙跳算法［J］.计算机工程与应用，2012，48(8):48-50.

［5］唐德玉，蔡先发，齐德昱，等.基于量子粒子群搜索策略的混合蛙跳算法［J］.计算机工程与应用，2012，48(29):29-33.

［6］李希婷，孙 璐，钱永亮，等.基于改进混合蛙跳算法的SVM 分类算法［J］.信息化研究，2011，37(5):41-44.

［7］Kenndy J，Eberhart R C.Particle Swarm Optimization［C］// Proc.of IEEE Int'l Conf.on Neural Networks.Perth，Australia:［s.n.］，1995，4(2):1942-1948.

［8］Sun Chaoli，Zeng Jianchao，Pan Jengshyang.A New Method for Constrained Optimization Problems to Produce Initial Values［C］//Proc.of Chinese Control and Decision Conference.Guilin，China:［s.n.］，2009:2679-2681.

［9］Storn R，Rrice K V.Differential Evolution——A Simple and Efficient Heuristic for Global Optimization over Continuous Space［J］.Journal of Global Optimization，1997，11(4):341-359.

［10］李爱国，覃 征，鲍复民，等.粒子群优化算法［J］.计算机工程与应用，2002，38(21):1-3，17.

［11］程 适，史玉回.基于L1 范式的粒子群算法群体多样性研究［J］.计算机科学，2011，38(7):190-193.

［12］刘悦婷，赵小强.一种自适应惯性权重的混合蛙跳算［J］.计算机工程，2012，38(12):132-135.