基于DCFT 的Chirp 矩阵采样重构算法

柏路平，马丽红，李青龙

(华南理工大学电子与信息学院，广州 510640)

1 概述

压缩采样的目的主要是用尽可能少的采样数据获取稀疏信号［1-2］，它将一个k-稀疏(非零元个数为k)信号向量X 在采样矩阵Φ 上投影，得到一个只有少量数据的采样信号向量Y。可压缩非稀疏信号在某些正交变换下只保留少量的大系数，也可视为稀疏信号，其余去掉的接近于零的小系数，可看作信号上叠加的噪声。

从X 得到Y 是一个简单的线性投影过程，然而从Y 准确重构X 却是一个通过最佳原子选择估计信号的非线性过程。首先，最小l1范数优化［3］和l0范数贪婪迭代算法［4］是常用的重构方法;其次，只有任意列之间的相关系数很小的矩阵才能成为采样矩阵，并且需要满足k 阶受限等距性质(Restricted Isometry Property，RIP)［5］，才能以较大的概率保证准确重构X。RIP 性质要求Φ 的任意M 列组成的子矩阵具有近似正交矩阵的性质。在RIP 性质上随机矩阵是Φ 的最佳选择，高斯矩阵和伯努力矩阵列之间的相关性很小，能以最小采样长度满足RIP 性质［6］，但其在硬件电路中难以实现，需要很大的存储空间存放采样矩阵的随机元素，以及需要大量重复实验验证其统计性能［7］。

纠错码码字间的最小距离与压缩采样矩阵的列相关系数相似，因此，线性码成为确定性采样矩阵的主要构造方法。多项式矩阵是素数域GF(p)的r 阶多项式构造p2×pr+1的二进制稀疏矩阵，其任意两列相关系数最大为r/p，并且满足阶数为k ＜p/r +1的RIP 性质［8］。代数曲线矩阵是多项式矩阵的一般形式，选择合适的代数曲线能得到比多项式矩阵性能更好的矩阵［9］。二阶里德穆勒矩阵［10］将哈达玛矩阵作为采样矩阵的列块，满足统计RIP 性［7］，可利用快速哈达玛变换来加速重构。

由离散Chirp 序列构成的Chirp 矩阵采样，重构时可利用离散傅里叶变换快速算法(FFT)［11］。但由于chirp 信号交调干扰的存在，用离散傅立叶变换(DFT)相关检测方法，即用采样信号自相关的DFT最大的幅值及位置来估计Chirp 参数，Chirp 率、基频和幅值的估计误差会随信号稀疏度k 的增大而急剧增加。

本文提出基于DCFT 的Chirp 矩阵采样重构算法，在保留Chirp 矩阵的确定性，以及快速傅立叶变换加速重构的优点同时，能够增大可采样信号的稀疏度k 以及提高信号的重构精度。DCFT 将Chirp信号的频谱从一维扩展至二维，使Chirp 率相同而基频不同的分量不再相互干扰，比DFT 具有更高的频谱分辨率［12］。用DCFT 替代DFT 相关法来检测采样信号的最佳原子，可避免DFT 相关检测算法因交调干扰造成的原子误检测，最后用最小二乘法估计非零元的幅值。

2 DFT 相关检测重构算法的局限性

基于线性调频原理的Chirp 采样矩阵［11］，是由Chirp 率和基频顺序增加的离散Chirp 序列排列而成。设c，f 分别表示Chirp 率和基频，长为M 的离散Chirp 序列向量Vc，f可表示为:

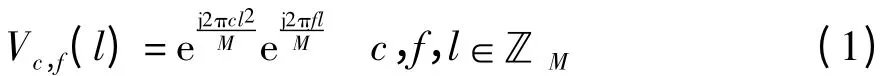
其中，(c，f)在整数域ℤM中共有M2种组合，将这M2个Chirp 序列按式(2)的顺序构成M × M2矩阵Φ:

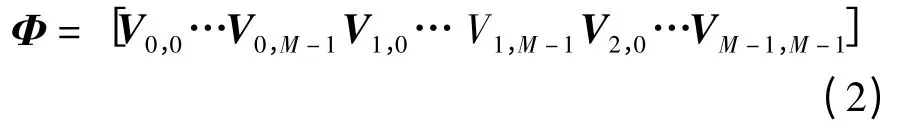
如果X 是k 稀疏的，则经矩阵Φ 采样得到的信号Y=ΦX 可表示为k 个chirp 序列的线性组合公式如下:

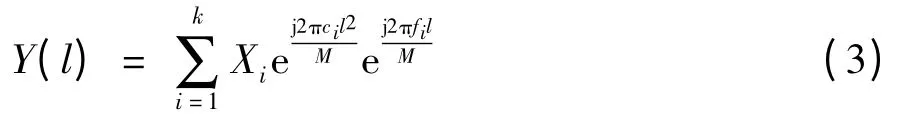
其中，Xi表示X 的第i 个非零元，则采样信号Y 的互相关向量F 具有下面的形式:

其中，时移T∈ℤM且T≠0，交叉项具有形式:

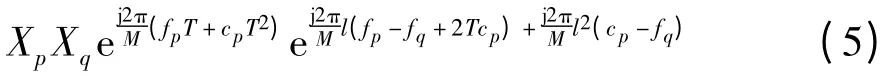
共有k(k-1)项，将引入交调干扰，其频谱不规则地分布在所有DFT 系数上。

DFT 相关检测重构算法的原理是:互相关向量F 的频谱在2ciTmod(M)的离散频率处为尖脉冲，如果M 是素数，那么从chirp 率到F 的DFT 系数是一个一一映射。所以，对F 做DFT 变换，在2ciTmod(M)的位置有一个峰值，可得到Chirp 率ci。然后将Y 乘以e-j2πcil2/M2，去除Chirp 率ci，Y 就变成具有单一谐波fi分量的信号，其DFT 峰值位置和大小分别对应一个基频fi和幅值Xci，fi，由此得到一个非零元的位置索引估计Mci+fi和幅值估计Xci，fi。然后将Y 用残差Y-Xci，fiej2πcil2/Mej2πfil/M代替，经过k 次迭代，就可按照幅值从大到小逐步得到Xi的位置与幅值。根据式(4)的时移T 的不同取值，文献［11］给出单时移和多时移的DFT 相关检测2 种重构算法，多时移DFT 相关重构算法具有更小的重构误差以及更强的抗噪性能。

用Chirp 矩阵采样时，DFT 相关检测算法重构的信号误差很大，并且对稀疏度k 较大的信号会因误差太大而无法重构。(1)DFT 算法的采样数为信号长度的根方可采样的信号稀疏度k 要比采样数小;(2)chirp 信号交调干扰的存在，DFT 相关检测算法没有考虑式(4)中的交叉项的影响。随着信号稀疏度k 的增加，组成采样信号的Chirp 分量个数也相应增加，而式(5)那样的交叉项个数却成平方增加，对重构结果的影响急剧增加。再用DFT 相关算法检测最佳原子以及简单地用频域fi幅值的平方根来估计非零元的幅值，重构误差也将急剧增加。

3 离散Chirp-Fourier 变换

DFT 将时域的离散谐波分量无交叉干扰地映射到频域，每个离散频率都与一个谐波一一对应，并且存在FFT 快速算法，所以DFT 成为频谱估计的主要手段。然而DFT 对于频率线性时变的Chirp 信号的参数估计却不太理想，因为不同Chirp 率和基频的分量在频域都有重叠。DCFT 将DFT 从一维扩展为二维，是DFT 的一般形式:

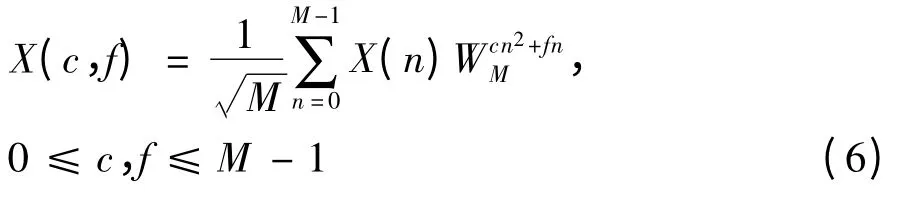
其中，M 为DCFT 变换的长度，WM=e-j2π/M;c 表示Chirp 率;f 表示基频。容易知道，当c 固定时，{X(c，f)}0≤f≤M -1为X(n)Wcn2M 的DFT 变换，因此FFT 也可用于X(c，f)的计算。DCFT 的一个重要性质为:

图1 (1×n2+3×n)长度为5 的DCFT 幅值分布

4 Chirp 矩阵采样重构算法

由式(4)和式(5)可以看出，采样信号Y 的所有Chirp 分量在其互相关向量F 的DFT 域都有交调干扰，而Chirp 率相同而基频不同的分量在DCFT 域中没有叠加，所以用DCFT 替代DFT 相关算法可以更准确地检测采样信号的最佳原子，进而减小重构误差。另外，在压缩采样中，稀疏度k 是信号的重要信息，为保证准确重构，采样数应随k 的增大而增大。在DFT 相关检测的重构算法中，采样数由信号长度N 决定，无论稀疏度为何值，采样数均为可采样的信号的稀疏k 非常有限。在这种情况下，增加采样数，以降低压缩效率换取重构性能是准确重构稀疏度大的信号的主要方法。

当M 为素数时，在单分量Chirp 信号的M 长DCFT 中，坐标(c0，f0)处的幅值为非(c0，f0)处最大为1。假设信号由等幅值的k 个Chirp 分量组成，当满足时，|X(c，f)|中最大k 个幅值就能以很大的概率分别对应所有的k 个Chirp 分量。用DCFT 来估计采样信号Y 的Chirp 参数时，变换的长度与采样数相等，所以为利用Y 的DCFT 变换中k 个最大的幅值所对应的原子索引来击中非零元的位置，采样数M 应增大为k2，但只有当作DCFT 变换的长度为素数时，才具有式(8)的性质，所以最终的采样数为大于k2的最小素数。

根据前面的分析，本文基于DCFT 的Chirp 矩阵采样重构算法的采样矩阵Φ 的元素为:

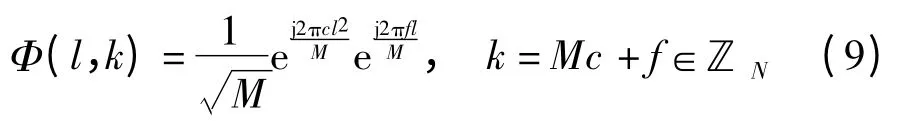
DCFT 重构算法的执行步骤为:

(1)计算采样信号Y 长为M 的DCFT 变换X(c，f);

(2)搜索|X(c，f)|中最大的k 个值的坐标(ci，fi)，记录位置索引集合Λ=∪k-1i=0{M·ci+fi}，从采样矩阵Φ 中提取Λ 对应的原子组成最佳匹配矩阵ΦΛ;

(3)用最小二乘法估计重构信号的非零元向量XΛ的幅值:

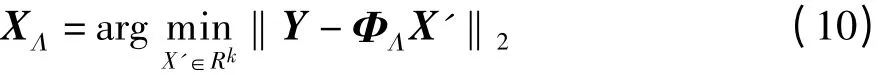
(4)在长度为N 的全零向量中位置索引为Λ 中的元素依次取XΛ中的元素就可得到信号X 的估计值Xt。

与DFT 相关检测重构算法相比，本文基于DCFT 的重构算法主要有3 个方面的改进:(1)用频谱分辨率更高的DCFT 代替DFT 相关算法检测采样信号的最佳原子和非零元的位置;(2)适当增加采样数至信号稀疏度的平方以换取重构性能;(3)提取最佳原子匹配矩阵ΦΛ，用最小二乘法求解非零元的幅度值，使重构的Xt与X 之间的误差达到最小。

5 实验性能与分析

为了验证DCFT 重构算法的性能，本文用Matlab 程序仿真一维稀疏信号的采样与重构过程，并用重构信号Xt与X 的相对误差:

来评估重构误差。为了与DFT 重构算法比较对相同长度和稀疏度的信号的重构性能，选择长度N=412=1 681 的测试信号，对于每个稀疏度k ∈{1，2，…，40}，非零元位置随机产生而幅值服从(0，1)上均匀分布的信号，用本文提出的采样和重构方法求得重构误差SE，并重复1 000 次实验，得到均方误差MSE。DCFT 重构算法的均方误差—稀疏度性能曲线如图2 所示。

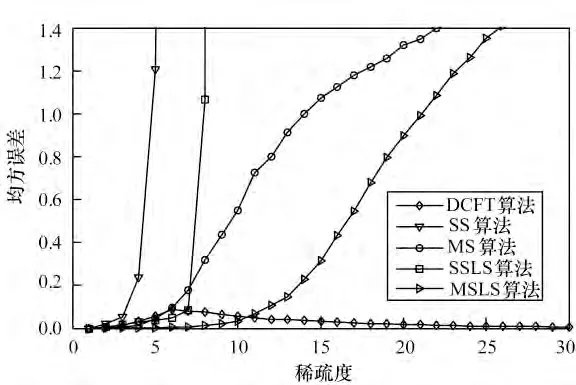
图2 DCFT 重构算法的误差曲线

为便于比较，2 种DFT 相关检测重构算法以及它们用最小二乘法优化后的误差性能曲线也在图中画出。优化过程是先用DFT 相关算法检测最佳原子，再用最小二乘法求解非零元的幅值，这样重构的信号具有更小的重构误差。

在图2 中，SS 和MS 分别表示单时移与多时移DFT 相关检测算法，SSLS 和MSLS 分别表示用最小二乘法优化后的单时移与多时移DFT 相关检测算法的误差曲线。可以看出，在稀疏度k 分别大于6和12 时，最小二乘优化后的单时移和多时移的DFT相关检测算法的相对均方误差已大于0.1，可视为重构完全失效。而DCFT 重构算法只在k=6 时有误差约为0.09 峰值，之后随k 的增加，误差逐渐减小。如果将误差小于0.1 的重构视为准确重构，则DCFT重构算法能准确重构的信号稀疏度k 扩大为DFT 算法的4 倍左右。

由于Chirp 采样矩阵可由信号长度N 和稀疏度k 唯一确定，重构时不需存储空间大小为M ×N 的采样矩阵，只需存储长为N 的DCFT 变换矩阵及重构信号Xt，因此重构空间复杂度为O(N)。FFT 变换的时间复杂度为O(MlogM)，而计算DCFT 变换只需要次FFT 变换，所以复杂度为O(Nlogk)，从N 个数里面搜索最大的k 个数的排序时间复杂度为O(kN)，解最小二乘的复杂度为O(k2M)，所以整个DCFT 重构算法的时间复杂度为O(kN)。当信号长为O时，其复杂度处于单时移DFT 相关检测的O(kMlogM)和多时移DFT 相关检测的O(kM2logM)之间，但优于最小l1范数中内点法O(M2N3/2)以及匹配追踪的O(kMN)时间复杂度。

6 结束语

本文提出基于DCFT 的Chirp 矩阵采样重构算法，采样时根据信号X 的稀疏度k，增加采样数以换取重构信号的质量;重构时，搜索采样信号DCFT 变换最大的k 个幅值，其坐标所对应的在采样矩阵中的原子即为信号X 的最佳匹配原子，最后用最小二乘法求解非零元素的幅值。对一维信号的采样和重构实验结果表明，与DFT 相关检测算法相比，DCFT重构算法具有更小重构误差。本文提出方法的采样数随信号稀疏度呈平方指数增加，虽然能准确重构稀疏度k 更大的信号，但与最佳的线性采样数相差较远，因此，保证重构质量的同时减少采样数成为下一步的工作目标。

［1］Duarte M F，Eldar Y C.Structured Compressed Sensing From Theory to Applications［J］.IEEE Transactions on Signal Processing，2011，59(9):4053-4085.

［2］马坚伟，徐 杰，鲍跃全，等.压缩感知及其应用:从稀疏约束到低秩约束优化［J］.信号处理，2012，28(5):609-623.

［3］Becker S，Bobin J，Candes E.NESTA:A Fast and Accurate First-order Method for Sparse Recovery［J］.SIAM Journal on Imaging Sciences，2011，4(1):1-39.

［4］Dai W，Milenkovic O.Subspace Pursuit for Compressive Sensing Signal Reconstruction［J］.IEEE Transactions on Information Theory，2009，55(5):2230-2249.

［5］Davenport M A，Wakin M B.Analysis of Orthogonal Matching Pursuit Using the Restricted Isometry Property［J］.IEEE Transactions on Information Theory，2010，56(9):4395-4401.

［6］Candes E J，Tao T.Near-optimal Signal Recovery Form Random Projections:Universal Encoding Strategies［J］.IEEE Transactions on Information Theory，2006，52(12):5406-5425.

［7］Calderbank R，Howard S，Jafarpour S.Construction of a Large Class of Deterministic Sensing Matrices That Satisfy a Statistical Isometry Property［J］.IEEE Journal of Selected Topics in Signal Processing，2010，4(2):358-374.

［8］Devore R A.Deterministic Constructions of Compressed Sensing Matrices［J］.Journal of Complexity，2007，23(4-6):918-925.

［9］Li Shuxing，Gao Fei，Ge Gennian.Deterministic Construction of Compressed Sensing Matrices via Algebraic Curves［J］.IEEE Transactions on Information Theory，2012，58(8):5035-5041.

［10］Howard S D，Calderbank A R，Searle S J.A Fast Reconstruction Algorithm for Deterministic Compressive Sensing Using Second Order Reed-Muller Codes［C］//Proceedings of the 42nd Annual Conference on Information Sciences and Systems.Princeton，USA:IEEE Press，2008:231-239.

［11］Applebaum L，Howard S，Searle S.ChirpSensing Codes:Deterministic Compressed Sensing Measurements for Fast Recovery［J］.Applied and Computational Harmonic Analysis，2009，26(1):283-290.

［12］Xia Xianggen.Discrete Chirp-fourier Transform and Its Application to Chirp Rate Estimation ［J］.IEEE Transactions on Signal Processing，2000，48 (11):3122-3133.