广义预测控制在机组控制系统中的仿真研究

焦 军

大唐临清热电有限公司 山东 临清 252600

0 引言

广义预测控制算法（Generalized Predictive Control，简称GPC）是汲取多种控制算法的优点，在预测控制算法的基础上提出的，此种控制算法的数学模型是通过推导控制律参数而获取，在理论研究和实际应用中都得到了重视［1］。分别采用PID控制算法、多变量动态矩阵控制算法和多变量广义预测控制算法对300MW机组70%负荷点处定压运行进行仿真研究，分析了在此种工况下三种控制算法的优劣性［2］。

1 多变量广义预测控制算法

以实际工业生产过程为基础并结合相关的理论知识提出了预测控制算法，与传统的PID控制相比，预测控制具有自身的优势。

如图1所示为预测控制结构图，由图1可见预测控制不仅利用了系统输出值与预测值的偏差，更重要的是利用了预测模型来预估过程未来的偏差值，并不断的进行滚动优化直至获取系统最优输入值，这也是预测控制优于其他控制方法的地方［3］。

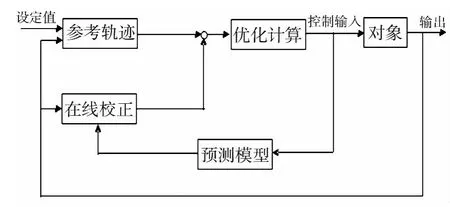
图1 预测控制结构框图

广义预测控制算法是在预测控制的基础上提出的，此算法保留了预测控制算法的诸多优点，比如较高的控制品质和良好的鲁棒性能等，并且广义预测控制算法也在此基础上做了改进和优化，可获得更好的控制效果。广义预测控制中被控对象的数学模型由离散差分方程式（1）所示［4］。

其中 A（z-1）、B（z-1）和 C（z-1）是后移算子 z-1的多项式，表示为：

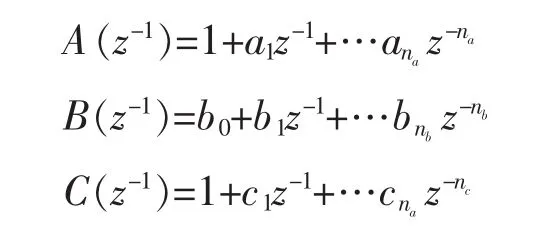
上式中，ξ（t）为均值等于零、方差等于 σ2。

Δ为差分算子且Δ=1-z-1；

u（t）为受控对象的输入值；

y（t）为受控对象的输出值；

性能指标函数由式（2）［5］；

σ为外部环境对系统的干扰值。

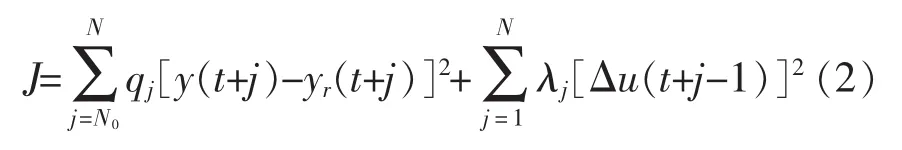
其中，Δu（t+j）＝0，j=Nu，…，N，N 为预测时域的最大长度；Nu为控制时域长度，在Nu步后控制量稳定，不受其他量的影响，yr（t+j）为系统设定的参考轨迹。qj为控制对象输出预测误差，λj为控制对象增量加权系数序列。

为简化预测模型的建立过程引入Diophantine方程，并且在第 j步后输出 y=（t+j）的最优预测值［5］：

为便于书写，省去以下各式中的算子z-1，同时用 Fj（z-1）左乘式（1）、（3）和（4）得到：

式中 Fjξ（t＋j）为 t时刻时对系统的干扰，可将t＋j时刻 y（t＋j）的最优预测值表示为：

由以上对广义预测控制算法最优预测值公式的推导可以看到此算法在滚动优化过程中可获得较高的性能指标，并且此种算法的反馈校正策略和数学模型的形式方面与其他算法有较大的差别。

2 机组受控对象模型

一般电厂单元机组的受控对象较为复杂，是一个多输入多输出的控制系统，需要考虑到的参数很多，并且受控对象具有较高的耦合性和相互关联性。为了便于对控制系统进行分析，在保证满足控制要求的前提下，将受控对象的模型简化为两输入两输出的系统如图 2 所示［6］。

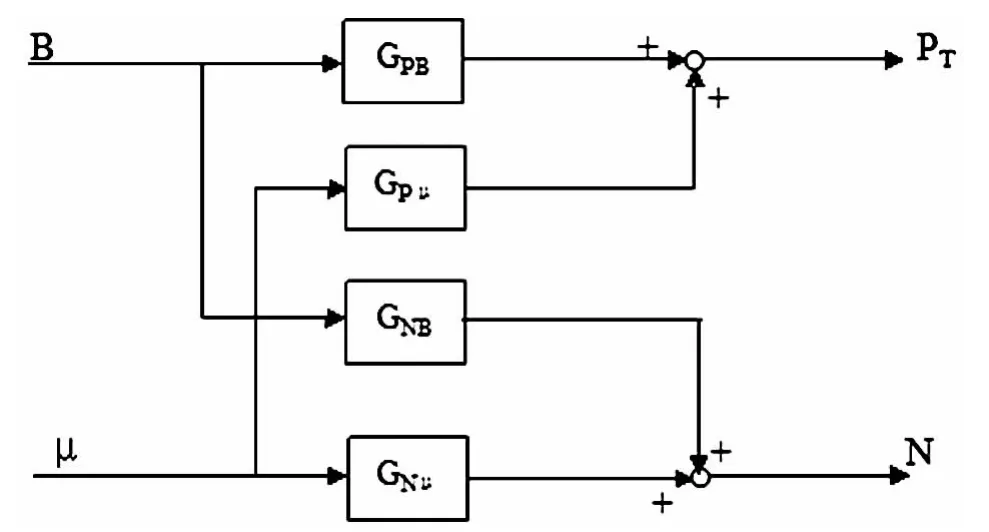
图2 单元机组受控对象模型

由图2可见将单元机组复杂的多输入多输出的控制系统简化成了有锅炉的给煤量B和汽轮机调节门开度为输入，机前压力PT和发电功率N为输出的模型，并且此简化模型的动态特性由线性常系数多变量传递函数式（6）和（7）来描述［6-7］：

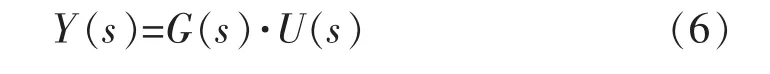
其中

式中 Y（s）是被控量矢量，U（s）是控制量矢量，G（s）是传递函数矩阵。

控制对象的动态模型选取为300MW直流锅炉燃煤机组， 量纲系数为：ΔPT，MPa；ΔN，MW；ΔB，t／h；Δμ，%（汽轮机同步器开度）在机组 70%的负荷点上，参考清华大学吕崇德先生提出的300MW火电机组数学模型，并且将此模型离散化得到动态数学模型为［8］：

通过调节汽机调节门开度Δμ可快速的改变机组被控量机前压力PT和发电功率N，但是在机组机前压力的变化范围和速度上受到局限；被控对象的输出控制量PT和N在锅炉控制量ΔB的作用下响应较为缓慢；可见在热惯性方面锅炉侧比汽机侧要大，这样单元机组被控量的响应速度就接近锅炉控制量的响应速度。

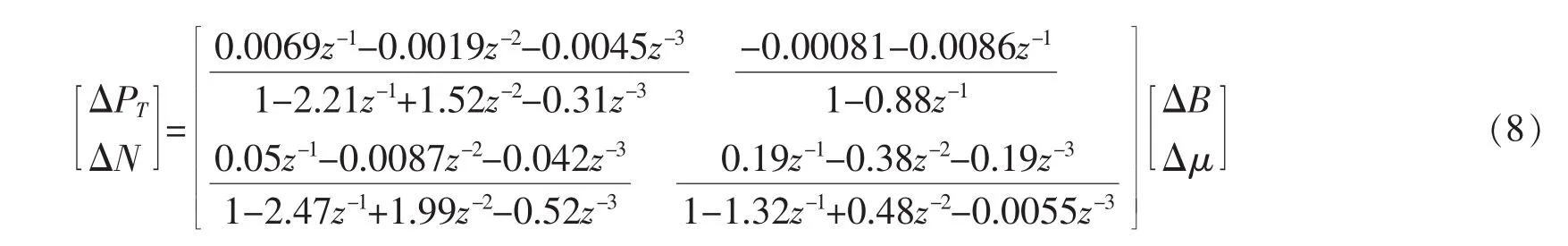
3 控制方案仿真研究

将广义预测控制算法添加到机组70%负荷点上的动态数学模型中，即将此算法应用到机组受控的动态模型中，比较机组在定压运行的工况下采用PID控制算法、多变量动态矩阵控制算法和广义预测控制算法的情况下机组的响应速度和鲁棒性。利用MATLAB仿真软件，模拟出三种控制算法的响应速度和鲁棒性曲线。

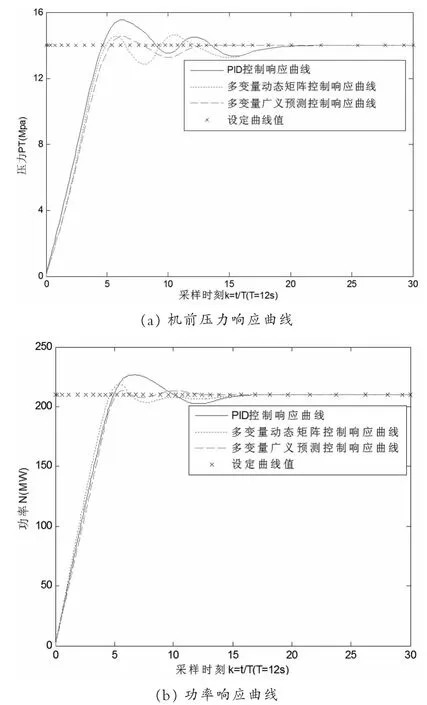
图3 定压运行，汽机带定负荷响应曲线

选取主蒸汽压力设定值为PT0=14.2MPa，在此定压力方式下的功率设定值N0为机组70%负荷点即N0=210MW［9］。采用三种不同控制算法机组的机前压力和功率相应的仿真曲线如图3所示。

由图3可以看到，在定压运行，汽机带定负荷工况下：

1）采用PID控制算法时，主蒸汽压力响应的过渡过程时间t1=18T，主蒸汽压力响应最大超调量的绝对值Mp1=2MPa，功率响应时间t2=20T，功率响应最大超调量的绝对值Mp2=18MW；

2）采用多变量动态矩阵控制算法时，t1=16T，Mp1=1MPa=1，t2=15T，Mp2=20MPa，且存在稳态误差；

3）采用多变量广义预测控制直接算法时，t1=8T，t2=10T，且系统输出均可达到无超调地跟踪设定值。

可见在此工况下，通过比较三种控制算法在机组控制系统中的应用所得的仿真曲线，采用多变量广义预测控制算法，在保持机前压力的平稳性方面和满足功率响应的快速性方面，都得到了较为理想的控制效果［10］。

要评价一个控制系统控制性能的好坏，控制系统的鲁棒性也是必须要考虑的问题，因此在此300MW单元机组70%负荷点处定压运行的工况下，采用PID控制算法、多变量动态矩阵控制算法和多变量广义预测控制算法时对控制系统的鲁棒性进行仿真研究，并对仿真效果进行比较分析。

在k=70s时输入阶跃扰动，取压力设定值PT0=14.2MPa，取功率设定值N0=210MW。

采用三种控制算法在系统受到扰动后得到的仿真曲线如下图5所示。

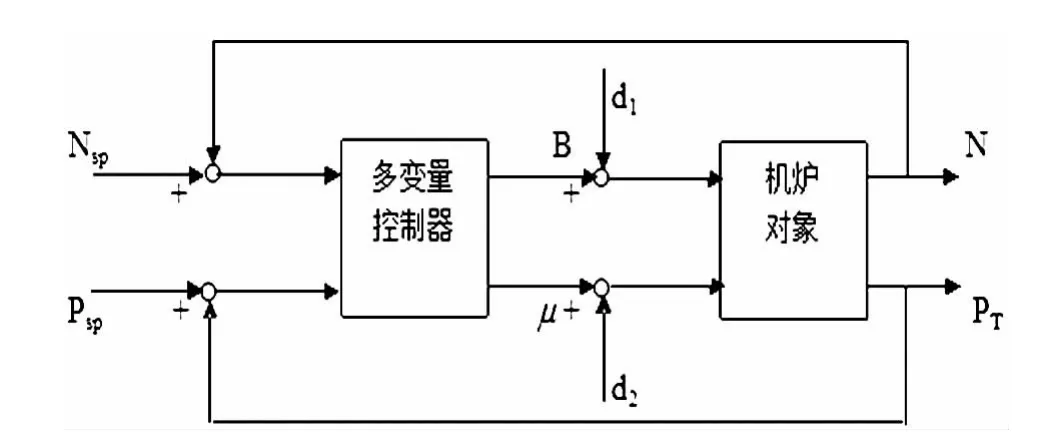
图4 扰动作用示意图

图5 定压运行，汽机带定负荷，在k=70s时刻受阶跃扰动的响应曲线

由图5可以看到在定压定负荷的工况下，机组在k=70s受到一阶扰动后，系统的波动情况为：

1）采用PID控制算法时，主蒸汽压力响应最大超调量的绝对值Mp1=3MPa，功率响应最大超调量的绝对值Mp2=10MW；

2）采用多变量动态矩阵控制算法时，Mp1=2MPa，Mp2=7MW；

3）采多变量广义预测控制直接算法时，Mp1=1MPa，Mp2=5MW。

通过对机组鲁棒性能的仿真研究可见，采用广义预测控制算法相比于PID控制算法、多变量动态矩阵控制算法单元机组在克服外界扰动所带来的影响重新跟踪设定机前压力和设定功率方面，此种控制算法相应时间短，波动幅度小，具有较好的鲁棒性。

4 总结

分析了多变量广义预测控制算法机理，将此种算法应用到单元机组的控制系统中，以300MW机组为研究对象，选取机组在70%负荷点机组定压运行的工况下，分别采用PID控制算法、多变量动态矩阵控制算法和广义预测控制算法对机组的响应速度和鲁棒性进行了仿真研究和比较分析，验证了广义预测控制算法优良的控制性能。

［1］舒迪前.预测控制系统及其应用［M］.北京：机械工业出版社，1996.

［2］杜之正.预测控制在电厂协调控制系统中的研究［D］.保定：华北电力大学，2012.

［3］ 李国勇.智能控制及其 MATLAB 实现［M］.北京：电子工业出版社，2005.

［4］曹楠.多变量广义预测控制在单元机组协调控制系统中的应用研究［D］.北京：华北电力大学，2000.

［5］罗辑，曹建国等.基于广义预测控制的综合控制算法设计与仿真［J］.自动化技术与应用，2004，23（2）：10-14.

［6］吴宝琴.广义预测控制在协调控制系统中的应用［D］.保定：华北电力大学，2006.

［7］杨亮.单元机组协调控制系统分析及先进控制策略研究［D］.保定：华北电力大学，2008.

［8］吕崇德，任挺进，姜学智等.大型火电机组系统仿真与建模［M］.北京：清华大学出版社，2002.

［9］吴春芳.广义预测控制在热工过程中的应用［D］.北京：华北电力大学，2004.

［10］ X.J.Liu，L.X.Niu.Feasible Constrained Nonlinear Predictive Control on Power Plant［J］.American Control Conference，2008，32（6）.

［11］ XiYugen，LiShaoyuan.Fast Algorithm of Constrained Model Predictive Control ［J］.Journal of Shang Hai Jiao Tong university，2001，35（11）.