改进Logistic映射的动力学特性

(杭州电子科技大学电子信息学院，浙江 杭州310018)

0 引 言

混沌具有随机性和不可预测性，可用以产生性能良好的伪随机序列，以替代传统的伪随机序列而应用于密码系统和保密通信等领域之中[1]。离散混沌由于其算法简单及处理时运算速率快而在混沌应用中得到了广泛的研究[1-3]，其中Logistic映射是一个在理论和应用上研究最早和应用最多的一种离散映射，使其成为一种典型的伪随机序列信号源。但Logistic映射只有一个初值和一个参数，且混沌参数范围和满映射区间都较小，致使其密钥空间不大，序列安全性较低。虽然迄今大量文献研究新混沌系统的构造[4-5]，或提出改进的混沌系统，但大多研究系统的基本动力学特性，很少基于应用背景深入研究如何提高扩展混沌映射区间和参数范围等。本文基于如何扩展混沌映射区间和系统参数区间，提出了一个改进的Logistic映射。对其动力学特性分析后发现，映射具有任意的参数区间、任意的混沌区间和任意的满映射区间，一定条件下还会出现恒定混沌现象。

1 改进的Logistic映射

Logistic映射有3种形式[5]，其动力学特性相类似。本文研究如下形式的Logistic映射:

该映射数学结构简单，把其作为一个伪随机信号源存在如下缺陷:式(1)只有一个参数，且映射参数区间较小，仅为μ∈[0，2]，其混沌区的参数区间更小，约为[1.4，2](包括其中的周期窗口)，导致其密钥参数空间很小;满映射区间较小，仅为I=[-1，1]，较小的映射区间在迭代过程中将使其数值变化率小，用其产生伪随机数时将导致序列码率低，式(1)映射轨迹和分岔图如图1所示。

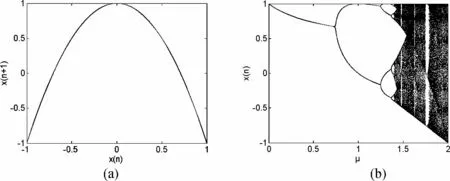
图1 Logistic映射轨迹和分岔图

为了探索更复杂的动力学特性，把式(1)改进如下:

式中，b ＞0，b∈R。分析表明，xn∈[-b，b]，μ∈(0，2/b)，b∈(0，2/μ)。从式(1)看出，减小参数b可扩展参数μ的范围，增加参数b可增大满映射的区间。

b=0.5时的分岔图和Lyapunov 指数谱如图2所示，改进前后该映射的参数范围由[0，2]扩展到[0，4];混沌区间由[1.4，2]扩展到[2.8，4]。b =2时的分岔图和Lyapunov 指数谱如图3所示，满映射区间由[-1，1]扩展到[-2，2]。

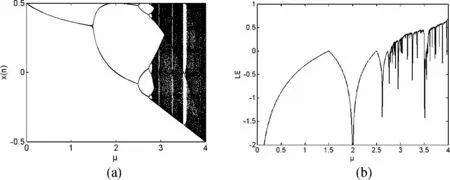
图2 b=0.5时，改进映射随参数μ 变化的分岔图与Lyapunov 指数谱

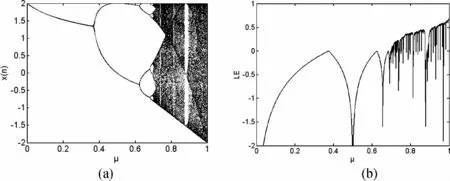
图3 b=2时，改进映射随参数μ 变化的分岔图与Lyapunov 指数谱

2 动力学特性分析

考察参数变化时映射的运动形态。解不动点方程x=b-μx2得其不动点:

不动点的稳定性满足:

不动点x2满足在整个参数区间都是不稳定的，故不讨论。而平衡点x1满足稳定的条件为:

故得:

解得:

周期2 轨道稳定条件为:

即:

在μ=5/(4b)时，又发生倍周期分岔，如此演化最终在1.401/b 后周期趋于无穷大，进入混沌状态，其混沌映射区间IC近似为:

例如，当b =0.5时，周期2 处的分岔参数为μ =3/(4b)=1.5，周期4 处的分岔参数为μ =5/(4b)=2.5，拟周期参数为1.401/b=2.802，混沌区间为IC=0.599/b，这些理论分岔参数都在图4(a)的分岔图中得到了验证。

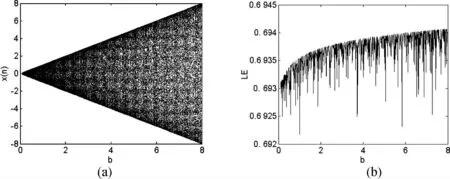
图4 改进的Logistic映射的分岔图与Lyapunov 指数谱

另一种最有意义的分岔规律是，当满足μ =2/b时，如图4(b)所示，出现一种恒定混沌现象，其Lyapunov 指数随着参数b的增加而略微增大，此种情况的混沌区间将趋于无穷大，这意味着有趋于无穷大的密钥空间，这在实际应用中将有重要的意义。

3 结束语

本文研究了一种改进的Logistic映射，该映射其满映射区间和混沌区间都得到了有效扩展，尤其在满足一定条件下可出现恒定混沌现象，参数在任意大的正数区间变化时，该映射都保持一种混沌状态，且Lyapunov是近似为恒量。用其作为信号源产生伪随机序列时可获得性能良好的序列和很大的密钥空间，在伪随机信号发生器的设计及其在保密通信和信息加密等需要伪随机序列的领域具有良好的应用前景。

[1]Narendra Singh，Aloka Sinha.Chaos-based secure communication system using logistic map[J].Optics and Lasers in Engineering，2010，48(3):398-404.

[2]Mamta Rani，Rashi Agarwal.A new experimental approach to study the stability of logistic map[J].Chaos，Solitons ＆Fractals，2009，41(4):2 062-2 066.

[3]Persohn K J，Povinelli R J.Analyzing logistic map pseudorandom number generators for periodicity induced by finite precision floating-point representation[J].Chaos，Solitons ＆ Fractals，2012，45(3):238-245.

[4]Thomas Curtright，Andrzej Veitia.Logistic map potentials[J].Physics Letters A，2011，375(3):276-282.

[5]Chen Shihliang，Hwang Tingting，Lim Wenwei.Randomness Enhancement Using Digitalized Modified Logistic Map[J].IEEE Transactions on Circuits and Systems Part II:Express Briefs，2010，57(12):996-1 000.