基于Copula函数的供应链上企业收益率相依性度量*

钱洪杰，吴会咏，杜 欣

(沈阳化工大学)

0 引言

Copula函数是将联合分布与随机变量的边缘分布结合在一起的一类函数族［1］．Patton A J［2］(2002)对 Copula 函数的特性做深入分析，并用其作为随机变量相关结构的度量函数，给出阿基米德Copula函数的分布函数和密度函数．韦艳华、张世英［3］(2008)总结金融分析中 Copula函数的应用方法，探讨在随机变量时变性的条件下Copula相关结构模型和变结构Copula模型．Wu Huiyong［4］(2011)用阿基米德 -Copula 函数建立依赖结构模型，对于六种主要外汇汇率的投资组合进行实证研究．

1 二元阿基米德Copula函数

阿基米德Gumbel Copula函数的密度函数为:

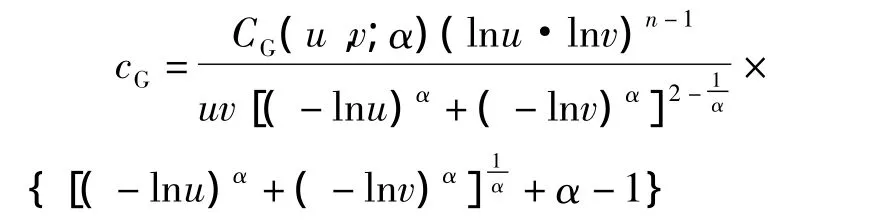
阿基米德Gumbel Copula函数的分布函数(如图1所示)为:

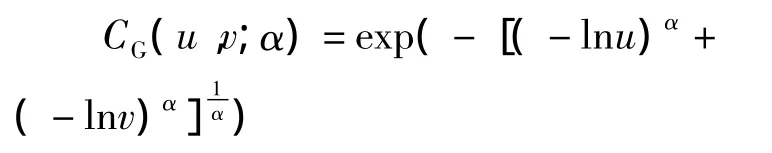
阿基米德Clayton Copula函数的密度函数(如图2所示)为:

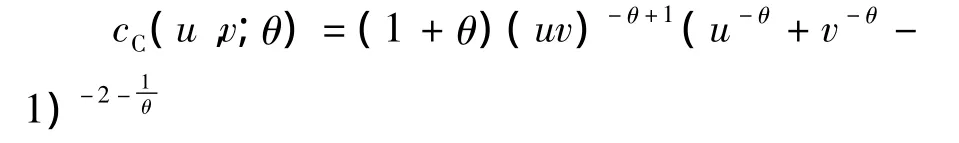
阿基米德Clayton Copula函数的分布函数为:

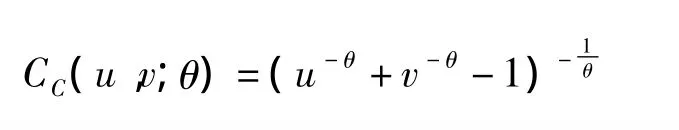
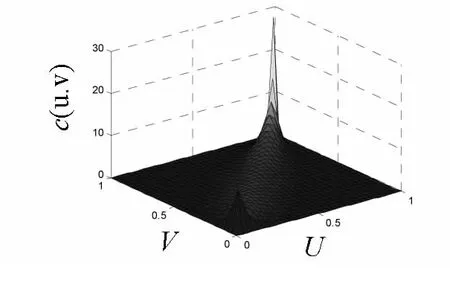
图1 Gumbel Copula密度函数

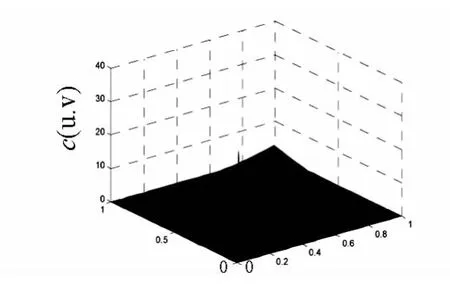
图2 Clayton Copula密度函数

2 利用Copula函数构建相依性测度模型的步骤

选取长春一东、一汽富维和福耀玻璃三家企业来研究，这三家企业同处于一汽集团的上游产品供应链上，收集三家企业的同期收益率作为样本(其中部分数据如表1所示)，利用阿基米德copula函数对其进行相关性分析．按照以下步骤构建Copula模型:

(1)确定三家企业收益率的边缘分布函数;

(2)通过比较选取最优的Copula函数度量相关结构模型;

(3)估计Copula模型中的未知参数．

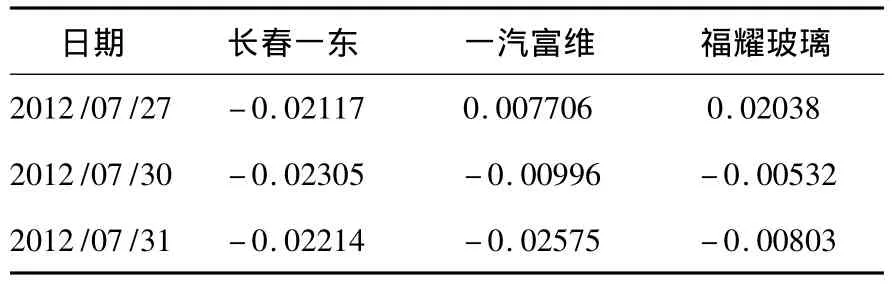
表1 长春一东、一汽富维和福耀玻璃的收益率部分数据

3 确定收益率的边缘分布

令X，Y，Z分别表示长春一东、一汽富维和福耀玻璃三家企业的日收益率，为确定三家企业日收益率的分布类型，对样本数据进行分布类型检验，结果如表2所示．若服从正态分布，样本的偏度应接近0，峰度应接近3．h=0为原假设，样本服从正态分布，h=1为拒绝原假设．由表2中的结果表明，只有一汽富维的收益率服从正态分布，所以在估计随机变量的分布时不能使用参数法，而应使用基于经验分布和核密度估计的非参数法．三家企业的概率分布如图3所示．

表2 样本数据的偏度、峰度和正态性检验

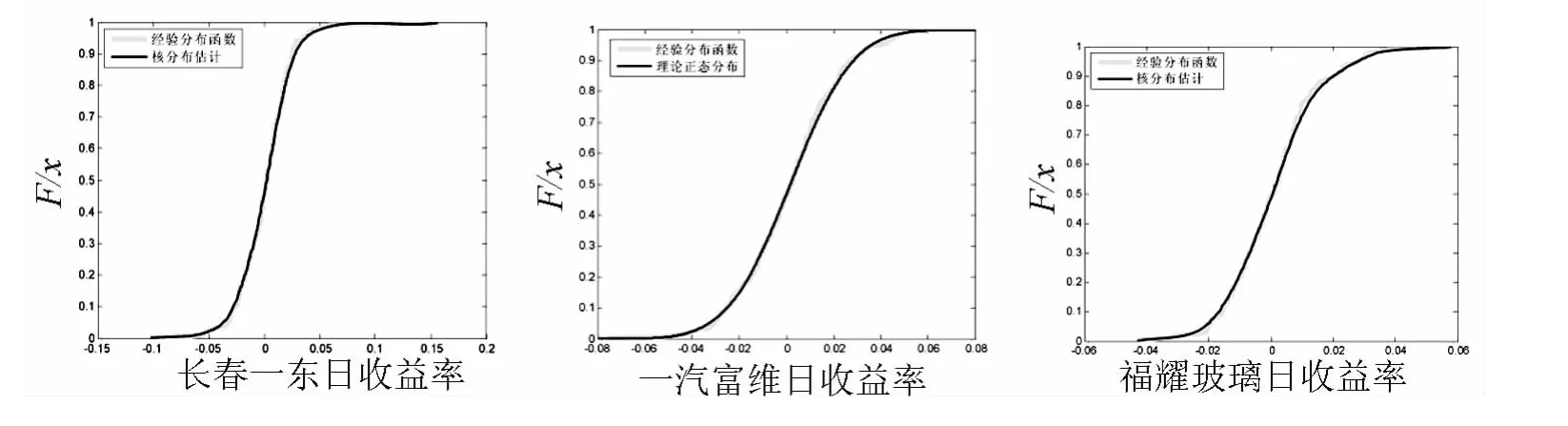
图3 收益率概率分布图

4 模型的参数估计与结果分析

用核分布估计出三个企业收益率的边缘分布，然后调用Copulafit函数估计Gumbel Copula和Clayton Copula模型中参数，调用Copulastat函数估计Kendall秩相关系数τ，并求出尾部相关系数．相关系数越大表明相关性越强．估计结果如表3所示．将参数带回模型中，就可得到相应的联合分布概率值．

由Gumbel Copula模型和Clayton Copula模型的Kendall秩相关系数的估计结果，对比得出一汽富维与福耀玻璃的相关度最高，其次是长春一东与一汽富维，最后是长春一东与福耀玻璃．

因为Gumbel Copula函数对上尾部的变化较为敏感，因而可以用于描述具有上尾相关性的供应链上企业间的相依度．Gumbel上尾相关系数估计结果表明一汽富维与福耀玻璃的相关联动较强．相依概率密度函数如图4所示．因为Clayton Copula函数对下尾部的变化较为敏感，因而可以用于描述具有下尾相关性的供应链上企业间的相依度．Clayton下尾相关系数估计结果也表明一汽富维与福耀玻璃的相关联动较强．相依概率密度函数如图5所示．

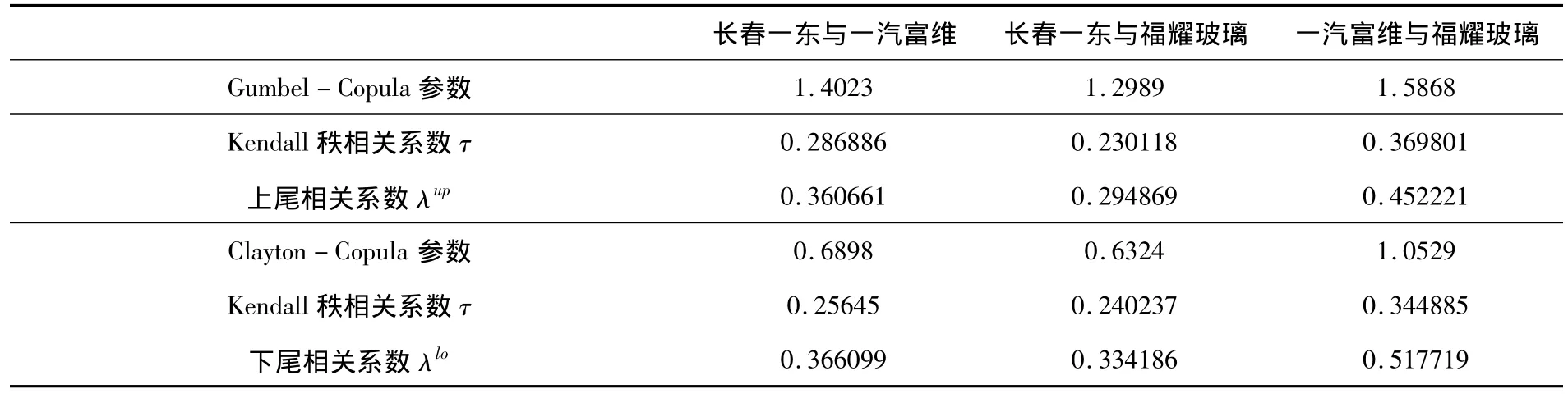
表3 模型的参数、kendall秩相关系数和尾部相关系数

图4 Gumbel Copula相关性概率密度函数图

图5 Clayton Copula相关性概率密度函数图

三个企业收益率的Copula密度函数的尾部峰值不同，说明三者之间的相关性也有区别．

5 模型的评价

对于长春一东、一汽富维和福耀玻璃的收益率的观测数据，构建了三个二元Gumbel Copula模型和三个二元Clayton模型，为了评价模型的优劣，引入经验Copula函数，经验Copula分布函数图如图6所示，通过比较六个模型与经验Copula的平方欧式距离，比较各模型间拟合的效果，选出更为适合的模型．平方欧式距离数据如表4所示．

表4 模型的平方欧式距离

通过对比平方欧式距离，数值较小者为拟合效果好，可以得出Clayton Copula对长春一东与一汽富维、长春一东与福耀玻璃的拟合效果更好，Gumbel Copula对一汽富维与福耀玻璃的拟合效果更好．

图6 经验Copula分布函数图

6 展望

Gumbel Copula函数对上尾变化十分敏感，Clayton Copula函数对下尾变化十分敏感，它们在度量尾部变化时都有各自的优势，但市场之间的相关关系就是变化的，不会限制于某种特定的模型．由于市场的相关性变化时非对称的，很难用一个简单的Copula模型来全面刻画其相关性，为了充分利用 Copula函数的特点，可以把具有不同特点的Copula函数组合起来，构成一个新的模型去描述具有复杂相关关系的事物．

［1］ 张尧庭．连接函数技术与金融风险分析［J］．统计研究，2002，(4):48-51．

［2］ Patton A J．Skewness，Asymmetric dependence，and portfolios［Z］．London School of Economics ＆ Political Science，2002．

［3］ 韦艳华，张世英．Copula理论及在金融分析上的应用［M］．北京:清华大学出版社，2008．

［4］ Wu Huiyong．The Supply Chain Model of Finance Payment，Which Made up of Providers，Central Enterprises and Distributors［J］．Information Technology Journal，2013，12(18):4699-4704．