岸桥调度的三维空间建模方法研究＊

张艳伟 周 万 郭 放

（武汉理工大学物流工程学院1） 武汉 430063）（武汉新港发展研究院2） 武汉 430063）

0 引 言

集装箱港口日常经营决策主要包括以下几个问题［1］：Q1，为到达船舶分配泊位；Q2，为到达船舶分配岸桥；Q3，确定岸桥在不同舱位的作业顺序；Q4，确定外部集装箱卡车的到达时间；Q5，内集卡的分配、调度及租用计划；Q6，内、外集卡的路径选择问题；Q7，内、外集卡在大门和岸边的派工策略；Q8，集装箱的箱位分配问题；Q9，场桥的分配与调度问题.

在以上9个问题中：Q1，Q2，Q3主要解决集装箱港口的岸边作业问题；Q4，Q5，Q6，Q7主要解决集卡调度问题（包括内集卡和外集卡），Q8，Q9主要解决堆场作业问题.在实际生产活动中，集装箱港口通常将岸边作业计划作为堆场作业问题及集卡调度问题的输入，因此在制定岸边作业计划时往往只需要考虑到港船舶的相关特性即可，而不用考虑集卡调度问题以及堆场作业问题对其可能产生的影响.

在集装箱港口的岸边作业问题中，Q1确定集装箱船在哪一段时间内停泊在码头的什么位置［2］，Q2确定各集装箱船在靠泊时间内的岸桥分配情况，Q3在Q1和Q2问题的基础上确定岸桥在各集装箱船不同舱位间的作业顺序.由于岸桥的分配情况（Q2）将直接影响到不同集装箱船所需的作业时间，而不同集装箱船所需的作业时间又对泊位分配计划（Q1）的结果产生很大影响，因而Q1和Q2通常需要一起考虑，被称为泊位与岸桥的联合分配问题（Q1+Q2）［3］.由于Q1+Q2的结果是岸桥调度问题（Q3）的输入，因此Q3不需要与Q1和Q2问题同时考虑，可以单独研究.

在岸桥调度问题的相关研究中，靳志红，李娜［4］研究了基于泊位计划的岸桥调度问题，并利用遗传算法对模型进行了求解.张亚辉，梁承姬［5］研究了离散舱位的岸桥调度问题.秦进，倪玲霖，王承娜等［6］研究了多船舶的岸桥调度问题，并利用模拟退火算法对建立的数学模型进行了求解.

1 建立三维空间

结合岸桥的实际工作情况，对岸桥调度问题做出如下假设.

1）每条船舶的靠泊时间以及该时间段内分配的岸桥数量已知（由Q1+Q2确定），每台岸桥都受到最早可利用时间的制约，并且所有岸桥的装卸效率相同.

2）集装箱船的每个舱位可以没有装卸任务，也可以包含多个装卸任务，每个装卸任务的工作量已知，同舱位的装卸任务之间存在作业顺序的制约，因为同贝位的装卸任务通常先进行卸船作业，再进行装船作业.每个装卸任务必须连续作业，同舱位的多个装卸任务之间可以连续作业，也可以不连续作业.

3）由于岸桥之间必须保持一定的安全距离，因而2个相邻的岸桥之间必须间隔至少一个舱位.

4）岸桥在固定轨道上运行，因而无论岸桥是否处于作业状态，岸桥之间都不能相互跨越.

将岸桥调度问题抽象成三维空间中长方体的位置决定问题，这种做法使得建立的模型更加简单.岸桥调度的三维空间模型见图1.

图1 岸桥调度的三维空间模型

三维空间中的每一个长方体都代表了一个装卸任务.X轴为时间序列；Y轴为船舶舱位号；Z轴为岸桥序号.长方体在X轴方向上的长度为装卸任务的作业量，在Y轴上的坐标为装卸任务所在的舱位，在Z轴上的坐标为装卸任务由哪一个岸桥完成.XOZ平面内的投影表示岸桥作业计划，即哪一个岸桥在哪一个时间段内为哪一个装卸任务服务；XOY平面内的投影表示不同舱位上的作业状态，即哪一个舱位上的哪一个装卸任务在哪一段时间内正在被服务.通过对XOZ平面，以及XOY平面内的投影设置相关约束就能够使岸桥调度满足实际生产中的限制条件.

2 变量定义和数学模型

为了方便建立数学模型，定义变量如下：I为装卸任务集合，i，j∈I；K为岸桥集合，k∈K；wi为任务i的装卸作业量，任务量单位为自然箱；xi为任务i开始装卸作业的时间，文中所涉及的时间单位均设定为处理一个自然箱所需要的平均时间；yi，任务i所在的船舶舱位号；zi，为任务i提供装卸服务的岸桥序号；bi，任务i完成装卸作业的时间；vij，当任务i的完成作业时间早于在任务j的开始作业时间，vij=1，否则vij=0.当同舱位的装卸任务之间存在先后顺序时，可以利用vij=1对装卸时间进行控制，这部分vij可以认为是已知量，其他的vij则为变量；uij，当uij=1时，任务i所在的船舶舱位号小于任务j所在船舶舱位号，并且为任务i提供装卸服务的岸桥序号小于为任务j提供装卸服务的岸桥序号.当uij=0时，舱位序号之间以及岸桥序号之间不需要满足大小关系的约束；Sik，当任务i由岸桥k提供装卸作业服务时，Sik=1，否则Sik=0；M为一个较大的实数，本文中取1000.

利用以上数学符号以及岸桥调度问题在三维空间中的几何意义，建立岸桥调度的整数线性规划模型如下.

目标函数：

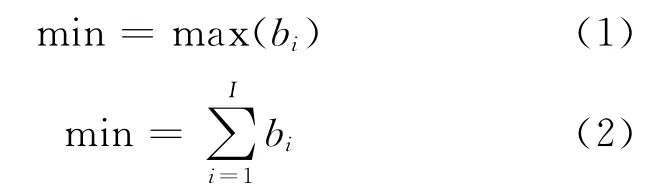
约束条件：

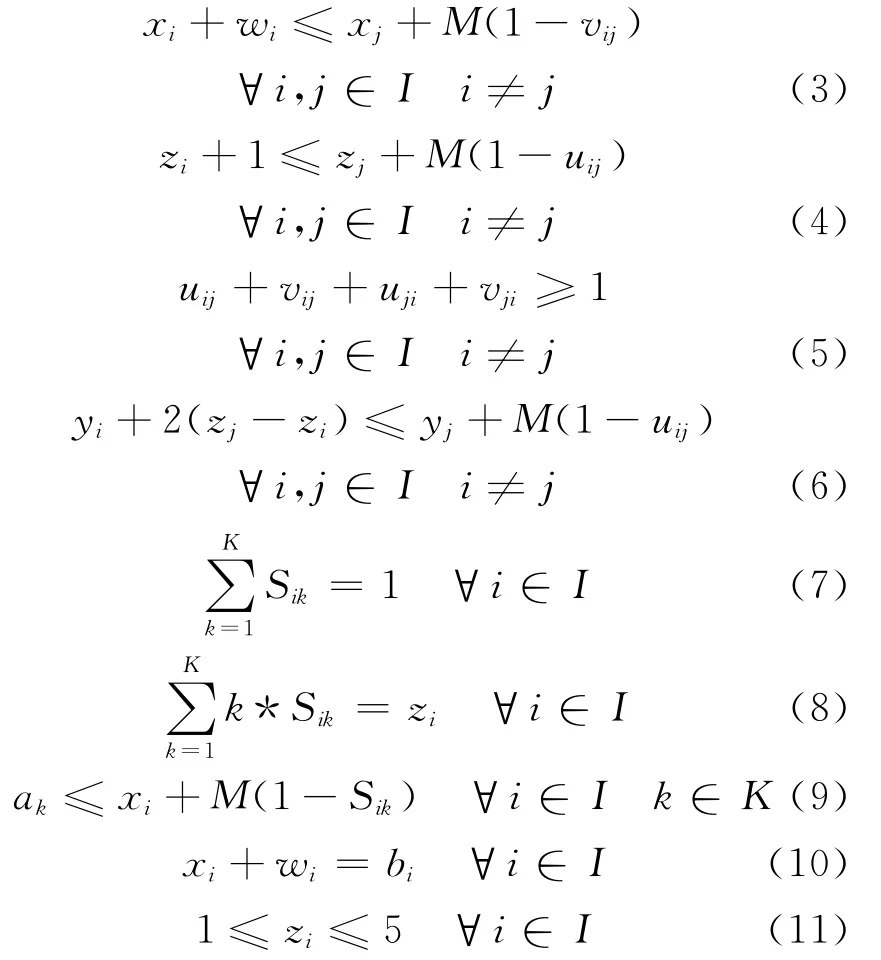
目标函数（1）表示最小化各装卸任务完成时间的最大值，因此该模型是一个最大、最小化问题.目标函数（2）表示最小化所有任务完成作业时间之和，为次目标函数.当目标函数（1）存在多个最优解时，可以利用目标函数（2）对岸桥调度问题进一步优化，得到更加合理的解.约束条件（3）～（6）用来实现岸桥调度问题中假设3）和假设4）的约束；约束（7）保证所有的任务有且仅有一个岸桥为其提供装卸服务；约束（8）表示岸桥作业状态与岸桥序号之间的关系；约束条件（9）表示所有的装卸任务都必须在对应岸桥的最早可利用时间后才能进行装卸作业.

3 算例分析

由于建立的模型是一个整数线性规划模型，因而该模型的求解比较容易，利用LINGO 软件可以方便地求解这一类问题.表1和表2给出了一个岸桥调度问题的算例，表示为一艘具有10个40in舱位，12个装卸任务的集装箱船分配了3台岸桥，需要确定岸桥在不同舱位间的作业顺序.假设岸桥装卸一个集装箱的作业时间为一个时间单位.

对于本文建立的多目标最大最小化数学模型，可以先不考虑目标函数（2）的最优化，并将目标函数（1）转化为约束条件，使优化模型转化为一个只有约束条件的混合组模型.增加的约束条件为

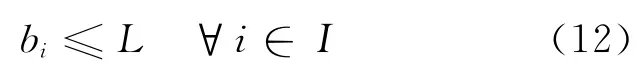
通过设定不同的L值来寻找目标函数（1）的最小值.利用Lingo软件的分支定界求解器，可以在1s之内求出混合组的可行解.当L=162时，混合组具有可行解，而当L=161时，混合组不存在可行解，因此目标函数（1）在最优解条件下的函数值为162.由于L=161条件下的可行解存在多个，因此目标函数（1）达到最小值时的最优解也有多个.将L值固定为162，把目标函数（2）作为惟一的目标函数，利用分支定界算法可以在6s内求出模型的最优解，目标函数（2）在最优解条件下的函数值为1198.在绝大多数情况下，模型的最优解惟一.利用LINGO 求得算例的最优调度方案见表3.

利用Excel软件将表3中最优化的结果绘制成岸桥调度的计划图（见图2）.为了进一步检验模型的有效性，并分析任务数、舱位数以及岸桥数对模型求解时间的影响，需要编制多个不同算例实验并进行求解.假设船舶贝位数的取值分别为10（3），14（4），18（5），22（5），括号中的数字表示允许同时作业的最大岸桥数量，岸桥数取值为3，4，5，任务数取值为10～30之间，当任务数较多时，分配的岸桥数量往往也较多.总共设计了54个算例.

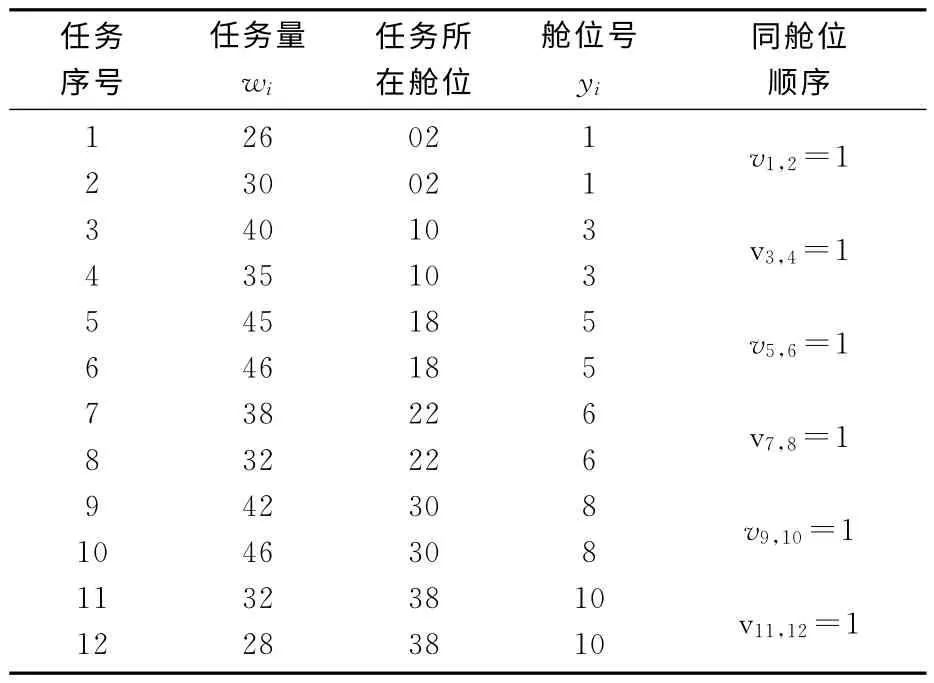
表1 装卸任务数据表

表2 岸桥工作数据表

表3 算例最优解结果

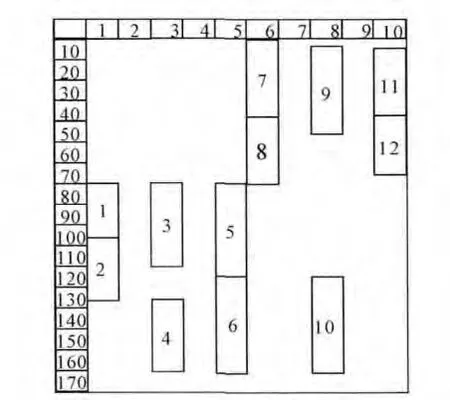
图2 岸桥调度求解结果

当算例的规模比较大时，往往很难通过LINGO 快速得出最优解，因而考虑通过设置合适的L值，得到可以接受的较优解，并比较分析在不同舱位数，任务数以及岸桥数等条件下，LINGO 求得较优解所需要的时间.假设某集装箱船的装卸任务量为450，分配3台岸桥为其服务.若所有岸桥在初始时刻就可以进行作业，则最优解不会小于150m（即L可以取得的最小值）.显然150 m为最优解可能达到的最小值（通常情况下最优解会大于这个值），令L分别取该值的105%和110%，即L=158m 或者165m.若L=158m 时存在可行解，则该可行解可以视为较优解，较优解与最优解（最优解大于或等于150m）的差值最大为5%；若L=158m 时不存在可行解，而L=165m时存在可行解，则较优解与最优解（最优解大于或等于158m）的最大差值仍为5%.比较不同条件下，LINGO 求得满足该L 限制的较优解的时间，见表4～表6.从表中的实验结果可以看出，在大多数算例实验中，可以在60s以内得到模型的较优解.在极少数情况下，模型较优解的求解时间会超过2min，即便如此，求解时间依然在可以接受的时间范围内.综上所述，该整数线性规划模型能够有效解决岸桥调度问题.

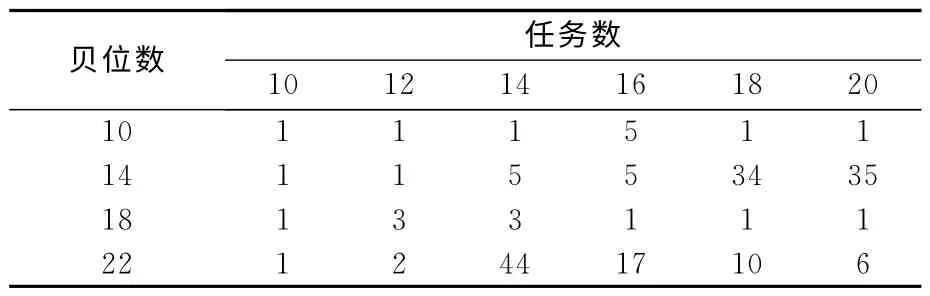
表4 算例实验的求解时间岸桥数＝3 s

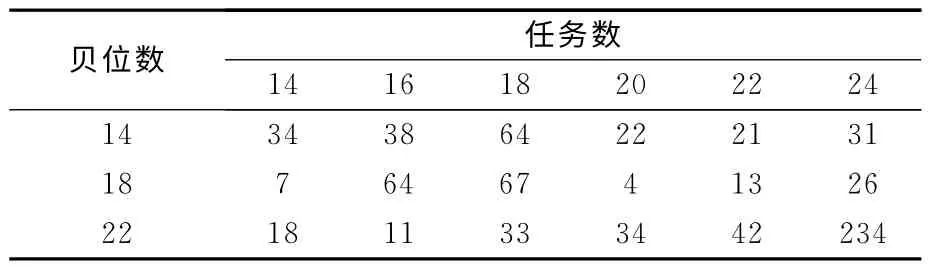
表5 算例实验的求解时间岸桥数＝4 s

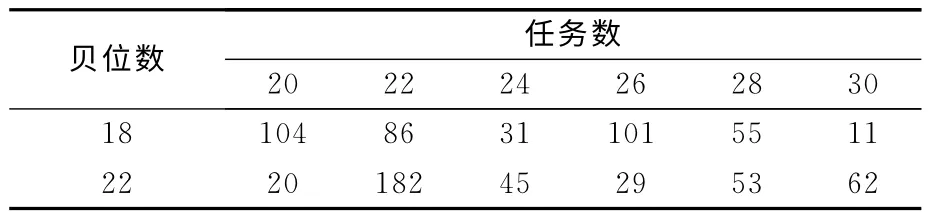
表6 算例实验的求解时间岸桥数＝5 s

4 结束语

本文针对集装箱港口实际生产中岸桥调度问题的特点，建立了以时间序列、船舶舱位号，以及岸桥序号为坐标轴的三维空间，并基于该三维空间建立了岸桥调度的整数线性规划模型.利用LINGO 软件可以求解出数学模型的最优解，当问题规模较小时，利用LINGO 软件求得模型最优解比较方便，当问题规模较大时，可以利用LINGO 软件在可以接受的时间内求得模型的较优解，通常情况下可以在1min左右求得与最优解差值在5%的较优解.算例实验结果表明，该三维空间建模方法能够有效解决岸桥调度问题.

［1］MURTY K G，LIU JIYIN，WAN Yatwah，et al.A decision support system for operations in a container terminal［J］.Decision Support System，2005，39：309-332.

［2］MOON K.Berth scheduling by simulated annealing［J］.Transportation Research，2003，37：541-560.

［3］KIM P.A scheduling method for berth and quay cranes［J］.OR Spectrum，2003，25：1-23.

［4］靳志红，李 娜.基于泊位计划的集装箱码头岸桥动态调度优化［J］.交通运输工程与信息，2011，11（3）：58-64.

［5］张亚辉，梁承姬.基于离散舱位的集装箱港口岸桥作业调度研究［J］.武汉理工大学学报，2012，34（5）：64-69.

［6］秦 进，倪玲霖，王承娜，等.集装箱码头岸桥调度优化模型及算法［J］.西南交通大学学报，2013，48（1）：184-192.