高等数学教学中创新思维的研究与实践

王 霞

（天津科技大学，天津 300222）

多年的教学实践我们发现，许多学生不会数学思维，学习数学只会死记硬背，表现在期末考试只要不出作业原题，不论考试题多么简单，就会出现预想不到的大面积不及格现象，如何在教学的过程中培养学生的数学思维能力，尤其是数学创新思维能力，是摆在我们一线教师面前一项紧迫任务。

一、数学创新思维的含义与特征

思维是人脑对外界事物间接、概括的反映，它反映的是事物的本质和内部规律。

创新思维是思维活动中最高层次的思维，它是主动地、创造性地发现新事物、提出新见解、解决新问题的思维形式。比如常说的“举一反三”、“触类旁通”等都属于创新型思维，即在学习中不因循守旧、善于独立思考与分析、能够积极主动探索新问题的一种思维方式。

数学思维是以数及形为思维对象，以数学语言为载体，以认识和发展数学规律为目的的一种思维活动。它是一般思维的特殊形式，主要包括抽象思维、形象思维、逆向思维，发散思维和直觉思维。即数学思维主要表现在意识力求抽象概括化、对象力求形式化、背景力求直观形象化、过程力求逻辑化、结果力求应用化。

数学创新思维是数学思维与创新思维相结合的产物，它是在已有的数学知识经验基础上产生新的思维结果，其特征表现在敢于探索，能够摆脱思维的常规束缚，产生新颖的、前所未有的思维成果。

二、高等数学内容蕴含丰富的数学创新思维

数学研究对象是思维的产物，它可以看成是一门思维的科学。数学本身又是一个逻辑体系，是由概念、性质、公式、法则，定理构成。以高等数学为例，其每一个概念都蕴含着逆向思维，即每一个概念都有其反面，如函数有界与无界、连续与间断、收敛与发散，在解决具体问题时，常用反证法来解决，或用逆否命题，如证明空集是任意集合的子集。逆向思维有利于克服思维定势的保守性，可寻求新的思路与方法，是一种创造性的思维。

类比思维在高等数学中处处可见，如二元及以上函数、极限、连续、可微的定义都类比一元函数得到；二、三重积分、第一型曲线、曲面的概念、性质都可由定积分的概念、性质类比得到。在解决从一元到多元，从一维到多维，从有限到无限，从离散到连续的问题时，类比的思维方法是非常有效的。

类比是特殊到特殊的思维方式，是根据两个或两类所考察的对象之间在某些方面有相同或相似的属性，并且其中一个对象还有另外的某种属性，从而推出另一对象也具有相同或相似的该种属性的思维。由于类比思维是提出新问题和做出新发现的一个重要源泉，也是探索解题思路的重要途径，故类比思维是创新思维的形式之一。

对多元函数求偏导时，将其中一个变量看成未知，其余所有变量均视为已知，即转化为一元函数求导。在对不定积分与定积分计算时，常用换元法，就是将要求的积分转化为可以用基本公式来计算的基本情形；二、三重积分的计算的思维方法是分别转化为两个、三个定积分来计算，微分方程部分也处处体现了转化的思维。

转化思维是通过某种变换过程将复杂的或困难的问题划归为与原问题等价的问题，而后者相对与前者较为简单或比较容易求解，转化的过程就是创新的过程，即转化思维是创新思维。

高等数学知识本身的应用就是创新思维，如用夹逼准则方法求数列的极限时，构造不等式的过程就是创新思维过程，还有正项级数的比较判别法，在找另一个正项级数的过程也是创新思维过程，再有设辅助函数、变量代换等，都是创新思维的具体体现。

三、数学创新思维教学实践

数学创新思维能力的培养一定要贯穿整个教学活动中，问题意识是思维的起点，是独立思考的标志，是创新的开始。学生的问题意识越强烈，学习过程中不断地产生“为什么？ ”、“是什么？ ”、“怎么办？ ”、“怎么变？ ”等，其思维也就越主动、越积极、越自觉，也就越有利于问题发现、问题发展和问题解决，反过来又能有力地促进学生数学思维能力的提高和创新意识的形成和发展。

如在讲导数概念时，让学生明确在均匀情况下凡是用除法定义的概念（物理量），在不均匀的情况下绝大多数都用导数来描述，还有生物种群的生长率和死亡率、放射性物质的衰变率、冷却过程的温度的变化率等必须用导数来度量，这就回答了为什么要学导数的概念。

导数是什么？从数学的角度，它就是个数，是函数的改变量与自变量改变量之比的极限值，是函数值随自变量变化快慢程度的一个度量；从物理角度，它是函数在一点的变化率；从几何角度，它是曲线过一点的切线的斜率；经济上，它表示边际。

导数存在的条件是什么？如果导数存在，如何求导数，即具体的求导方法？由于高等数学的主要研究对象是初等函数，由初等函数的结构自然得到下面的求导线索，如图1所示。

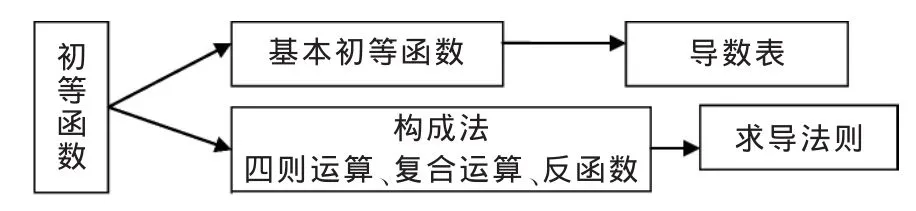
图1 求导线索图

导数有什么用？即在一个区间上可导的函数会有什么性质？这就是微分中值定理一章回答的问题。

在讲微积分基本定理这一节时，首先，让学生明白的基本问题是：什么样的函数可积分？怎样求可积函数的定积分？将定积分的概念类比导数的定义，可知：在均匀情况下用乘法定义的（物理）量，在不均匀的情况下一般都是用定积分，即导数与积分有互逆的关系。

学习数学，离不开数学思维，可以说数学的本质特性就是思维。我们经历了数学概念的引入，定理的发现，规律的探求等诸多过程。在这些认识活动过程中，是促使学生能够一步一步向前走，又能够使学生的智慧逐步提升，变得越来越聪明。即数学思维和数学思维方法，是数学学习过程中必须接触的内容，学生在学习高等数学的过程中，能力的提高主要在于对数学思维方法的掌握。

[1]王茹.国内数学创新思维能力研究述评[J].牡丹江教育学院学报，2008（4）.

[2]陈定元.高等教育中数学创造性思维的培养[J].安庆师范学院学报，2009（2）.

[3]杨锦伟，黄堃.基于高等数学创新思维的创新人才培养[J].教育与职业，2013（26）.

[4]聂东明.培养学生数学创新思维的教学策略[J].衡阳师范学院学报，2003（3）.

[5]赵世安.数学创新思维的心理机制及其能力的培养[J].广西民族学院学报，2001（2）.

[6]张文强.谈数学创新教育[J].锦州范学院学报，2002（2）.