基于单调性和凹凸性的一类级数敛散性判断

杜厚维

（长江大学一年级教学工作部，湖北 荆州434025）

秦超

（荆州市文星中学，湖北 荆州434000）

陈忠

（长江大学一年级教学工作部，湖北 荆州434025）

判别级数的敛散性方法比较多，将级数一般项或者部分和进行放缩，借助经放缩后级数的敛散性来判断原级数的敛散性，是其中方法之一。而函数的单调性、曲线的凹凸性都可用于证明不等式，下面笔者将利用函数单调性、曲线的凹凸性来判断一类级数的敛散性。

1 基本概念

定义1［1］设f（x）在区间Ⅰ上连续，如果对Ⅰ上任意2点x1、x2恒有：

则称f（x）在区间Ⅰ上的图形是凸的。

如果恒有：

则称f（x）在区间Ⅰ上的图形是凹的。

引理1［1］设f（x）在［a，b］上连续，在（a，b）内具有一阶和二阶导数，则：

1）若在（a，b）内f″（x）＞0，则f（x）在［a，b］上的图形是凹的；

2）若在（a，b）内f″（x）＜0，则f（x）在［a，b］上的图形是凸的。

引理2［1］设f（x）在［a，b］上连续， 在（a，b）内f″（x）＜0，则：

定义2［1］若级数收敛，则称级数绝对收敛。

引理3［1］若级数绝对收敛，则级数收敛。

引理4［1］若0≤un≤vn，级数收敛，则级数收敛。

2 主要结论

定理1 设当x∈［0，＋∞）时，f′（x）＞0，f″（x）＜0. 且F（x）为f（x）在［0，＋∞）上的原函数，则：

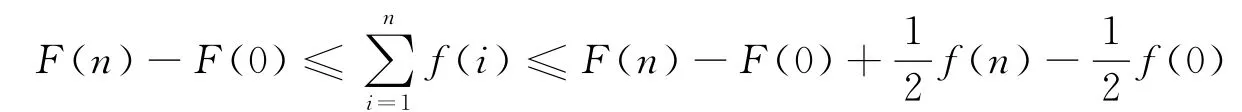
证明 由f′（x）＞0可知f（x）在区间［0，＋∞）单调递增，从而：

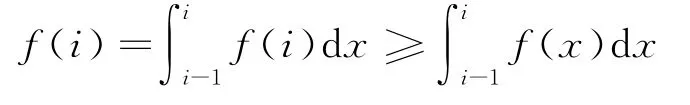
则：

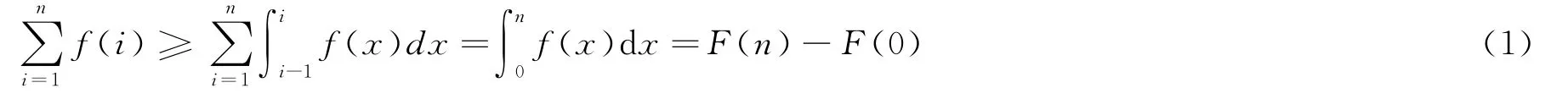
又：

由引理2，令a＝i－1，b＝i（i＝1，2，…，n），可得：

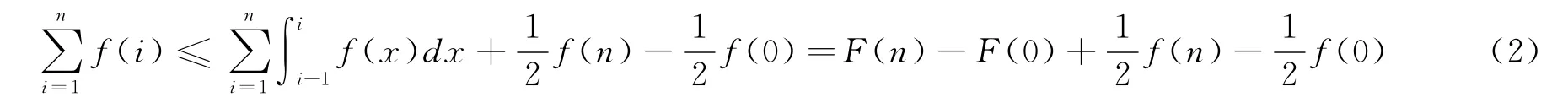
综合式（1）和式（2）即得定理1结论。

3 算例

解 令un＝

若0＜α＜1，令f（x）＝xα，则f（x）满足定理1的条件，故而级数收敛，由引理3，引理4知级数绝对收敛。

解 令：

可取适当正整数N0，当x∈［N0，＋∞）时：

由定理1得：

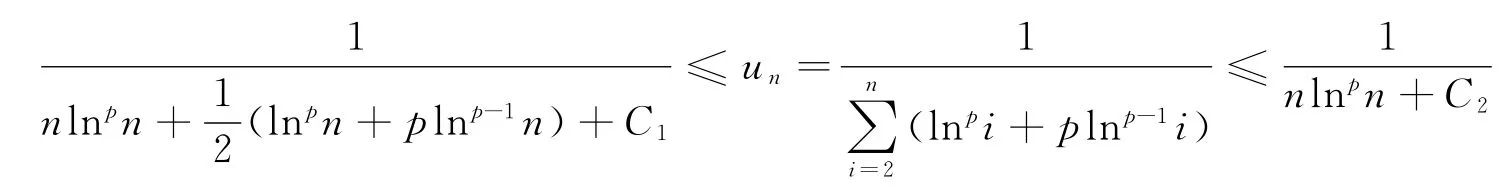
其中，C1，C2仅与N0相关。

例3［2］证明

由定理1有：

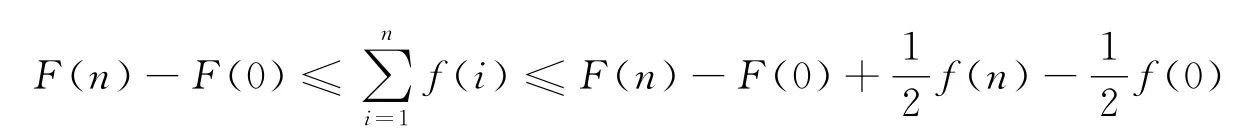
即得：

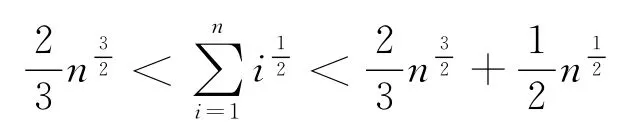
定理1是例3结论的一种推广。

除上述应用外，定理1还能与夹逼准则相结合，用于求极限。

［1］同济大学 .高等数学 ［M］.北京 ：高等教育出版社，2001.

［2］刘培杰数学工作室 .历届美国大学生数学竞赛试题集 ［M］.哈尔滨：哈尔滨工业大学出版社，2009.