一种新的矿山破碎站成品矿仓振动助流器的研制及应用

张春阳，曹平，仵锋锋，万琳辉

(1. 中南大学 资源与安全工程学院，湖南 长沙，410083；2. 长沙矿山研究院，湖南 长沙，410012)

矿石作为一种颗粒物质，在仓内长时间堆积，很容易因黏仓、起拱、卡斗而发生堵矿，严重影响矿山生产。在国外，例如 Anand等[1−2]对颗粒属性、筒仓结构、尺寸等因素下颗粒流动特征和力学关系进行了研究，指出颗粒流模型对优化颗粒流动和设备设计具有重要意义。在国内，李海旺等[3]用颗粒流程序分析了装、卸料中散料对仓壁的静、动态压力，发现与国家现行规范和ISO方法计算的异同；郑利娇等[4]认为料斗有效流通面积、加压气和流化气量会影响料仓内粉煤多股下料的流动性；肖国先[5]通过数值模拟得出了仓内散体流动、仓壁应力分布、改流体作用、湿颗粒流动的影响规律；陈汝超等[6]进行了有机玻璃料仓实验，发现出口直径、粒煤粒径和外水分对宽筛分粒煤在补气料仓中的下料特性有显著影响；秦雯等[7]通过室内模型实验，发现仓体流出过程中的离析现象主要是由于细料向下渗透，并分析了流出颗粒均匀性变化及影响因素；此外，肖国先等[8−13]对仓内颗粒物质也进行了研究。随着仓内颗粒物质流动特性及影响因素研究的推进，以这些研究成果为基础的助流设备研制已成为仓体工程的重要课题之一。传统的助流设备如底部振动助流器、空气炮、机器爪等对于高黏性铝土矿在实际生产中的助流效果不理想，如：底部振动助流器虽然改善了仓体底部矿石流动性，但振动波在传播过程中会不断衰减，振能难以有效到达仓体上部，对于大型仓体，有效助流范围十分有限；采用人工处理花费时间长，强度大，效率低，环境差，安全隐患极大。因此，研制适合高黏性铝土矿的除黏、破拱、防堵设备具有重要意义。

1 铝土矿黏仓及卡斗室内研究

1.1 模型实验

为了了解仓内铝土矿流动规律，找到合适的除黏、破拱方案，在现场取样后，以底部放矿为例，进行室内模型实验(该原理同样适合侧面放矿)。由于破碎站矿仓尺寸、形式已经固定，因此，实验主要研究不同水的质量分数和仓内壁摩擦因数下的流动特征。模型根据相似性原理，按矿仓实际尺寸缩制而成，几何相似比为1:12。

从现场采集矿石，用塑料袋密封，确保矿石水的质量分数不变。原形矿石的最大直径为30 cm，依据相似比，模拟实验矿石最大直径为3 cm。用孔径为3 cm的筛子对矿石进行筛分，用孔径小于3 cm的矿石进行室内放矿实验。

实验前先检测矿石中水的质量分数，3组矿石中水的质量分数分别为8.2%，9.5%和10.8%。实验表明：当水的质量分数为8.2%时，打开仓底阀门，有矿石稀疏流出；当水的质量分数为9.5%时，没有矿石流出；外力破拱后，矿石才继续流出。可见：当水的质量分数为9.5%时，在仓内已经结拱，矿石流出一段时间后又停止流动，说明又形成了新的拱，阻止了矿石继续流动，再次破拱后矿石又继续下落，前后破拱5次，才全部放完；当水的质量分数为 10.8%时，矿石流动性更差，前后需要至少7次破拱处理，且放矿后在底部四角仍有少量残余矿石，可见仓内死角处流动性最差。

此外，仓壁摩擦因素对矿石流动性影响也很大，尤其在仓内漏斗部分。模型通过在仓体漏斗壁面贴摩擦砂纸来实现。由于水的质量分数为8.2%时，矿石能够实现自流，因此，实验采用水的质量分数为8.2%的矿石。结果表明：采用摩擦因素较小的砂纸时，需破拱3次；采用摩擦因素较大的砂纸时，需破拱5次，仓体死角处矿石流动性最差。

1.2 实验分析

水的质量分数对矿石流动性影响很大。随着水的质量分数增大，矿石与仓壁间外摩擦因素增加，颗粒与仓壁间的吸附力增强，直至达到最大值，此时，矿石沿仓壁的流动性最差。当水的质量分数增加至某一限度后，就不再被矿石吸收，多余水以自由水的形式存在，在矿石和仓壁之间起润滑作用，使颗粒容易沿斗壁滑动，因而外摩擦因素反而降低。当实验矿石水的质量分数为8.2%～10.8%时，刚好处在外摩擦因素增大阶段，因此，仓壁处矿石流动性变差。

虽然水的质量分数增加使矿石颗粒间的内摩擦因素减小，但在初始阶段，矿石颗粒间黏结力加强。随着水的质量分数增大，矿粒间形成水膜，在气水界面产生表面张力的同时，存在颗粒间的胶凝物质和水分生成的水化结晶物产生黏结作用；当水的质量分数达到饱和状态之后，破坏了颗粒间形成的水膜和表面张力，黏结力又有所降低[14]。本实验中，当水的质量分数为8.2%～10.8%时，内摩擦角与黏结力相比，其影响相对偏小，导致仓内矿石的流动性变差，颗粒间的接触力变大，增加了仓内平衡拱的稳定性。

仓壁摩擦因素增大，使矿石与仓壁的摩擦力变大。在放矿过程中，仓内中间矿石流动最快，四周最慢，矿石在仓内受到摩擦力、黏结力的作用，在一定条件下形成平衡拱。由于拱承受上部荷载，所以，传给拱脚以力F，该力可以分解为垂直分力N和水平分力P[15](图1)。对于稳定拱，力F由仓壁处矿石与仓壁摩擦力平衡，因此，仓壁摩擦因素增大导致拱角承载力增大，破拱难度加大。

图1 拱的形成原理及作用力Fig. 1 Arch formation principle and force

2 振动助流机理分析

振动放矿是借助振动器振动和矿石自身重力，强制矿石自漏斗放出的放矿方法[16]。目前，振动放矿都是在仓底部安装振动器，振动在矿岩中以波的形式传播。传播的波有纵波和横波2种，纵波的波速可用下式计算：

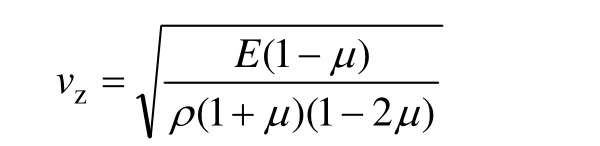
式中：νz为纵波速度，m/s；E为松散矿石的动弹性模量，Pa；μ为松散矿石的泊松比；ρ为松散矿石密度，kg/m3。

横波的波速可用下式计算：

式中：νh为横波速度，m/s。由于所有矿石获得的振动强度并不相同，与振动器距离越近，振幅越大，远离振动器时振幅减小，并逐渐趋近于 0。这主要是振动脉冲在向外传播过程中，振能消耗于克服重力、摩擦力以及转换为不可恢复的变形能，使振能在传播中逐层衰减，直至为 0，这种特性叫内阻尼，可用“衰减系数”表示，其表达式为

式中：Kz为松散矿石振能衰减系数；νb为振动波速，m/s；N为振幅对数递减率；ƒ为振动频率，1/s。

2.1 振动助流除黏作用

由于水的作用，矿石间因黏结而结块，靠近漏斗壁的矿石受到储存矿石压实影响，被挤压在漏斗仓壁上，并与仓壁紧密黏附在一起，容易在仓内漏斗附近形成压缩小漏斗，使仓内有效断面减小：因此，为了确保高黏性矿石顺利放出，应尽可能保证放矿口有效断面尺寸。

矿石的通过性常以通过系数表示[16]。通过系数是指放矿口的有效尺寸与最大块尺寸之比，其表达式为

式中：Kt为通过系数；hx为放矿口的有效尺寸，m；gk为最大块的尺寸，m。

振动放矿是通过增加放矿口有效断面，增大矿仓通过系数Kt，实现除黏，从而降低黏结成拱几率。在振动放矿条件下，矿石承受振动后，内摩擦因素减小，矿石颗粒黏结成拱的支撑力受到削弱，此时已不全靠重力放矿，能极大提高放矿效率。

2.2 振动助流破拱作用

拱基滑动使拱破坏的力系分析如图2所示[16]。首先对反作用力Wp的作用点取力矩，可得出反作用力的水平分量：

式中：Wp为反作用力的水平分量，N；hg为拱高，m；Gd为单位长度上的重力，N；lg为拱跨度，m。

反作用力的垂直分量为

式中：αp为反作用力与其水平分量的夹角；wc为反作用力的垂直分量，N。

反作用力的垂直分量的最大值为垂直载荷的一半，因此，成拱的条件为

矿块组拱示意图见图 2。振动放矿时，由于放矿口有效高度增大，使成拱的跨度增加，从而降低了矿块成拱的可能性，即使出现平衡拱，借助振能传播，也可削弱成拱的拱基，所以，不容易出现稳定平衡拱。同时，振动场内矿块间速度差小，能够有效降低矿石下降速度差引起的矿块成拱概率。虽然矿石在下降过程中，矿块间存在相互咬合的成拱条件，但由于振能的传播作用，有效降低了矿石间内摩擦角，从而阻止拱的形成，起到了很好的破拱效果。

2.3 仓内悬垂式振动助流器助流作用

虽然振动放矿具有很好的除黏、破拱效果，但是，传统的振动放矿装置安装在仓体底部，振能不能有效传播到仓内上部，因此，不能有效发挥振动助流作用。室内模型实验结果表明：仓内死角处矿石流动性最差，死角很容易因长期堆积矿石而黏仓，底部振动助流也无法优化仓内矿石的流动速度，矿石容易发生起拱。采用离散元软件PFC2D模拟仓内矿石流动规律，结果见图3。从图3可见：对于底部放矿矿仓，中间矿石流动性比四周大；侧面放矿矿仓离放矿口水平距离越远，流动性越差，且漏斗部分容易残留矿石，使仓漏斗部分有效断面尺寸降低，放矿难度增大。

图2 矿块组拱示意图Fig. 2 Ore arching schematic diagram

图3 仓内矿石流动特征模拟Fig. 3 Flow characteristics simulation of ore in hopper

3 仓内悬垂式振动助流器的研制

为了有效解决黏仓、起拱问题，可以采用插入式振动器，将其振动棒从料仓顶部直接延伸到料仓截面收缩部位，以达到改善矿石流动性目的。振动器结构由原动机、传动装置和工作装置3部分构成，见表1。工作装置是1个棒状空心圆柱体，通称振动棒，内部装有振动子，在动力源驱动下，振动子使整个振动棒产生高频微幅机械振动，振动棒由传动装置连接插入至料仓截面突然收缩部位，振动通过振动棒传递给矿石。在矿仓各死角处安装1个振动器，底部放矿矿仓可安装4个振动器，侧面放矿矿仓只需2个，其中底部放矿矿仓振动器安装如图4所示，振动器固定钢板安装如图5所示。

由于仓内矿石贮量大，矿石对设备的摩擦也大，放矿时软管的拉力和磨损比较严重。为了改善软管和振动棒抗拉耐磨性能，保护振动棒，在固定防滑耐磨链条下端将振动棒壁层加厚，将链条绕一圈焊接在振动棒上，并承担拉力，如图6所示。这样，振动器的使用寿命大大增强。当振动器仓内部分出现故障时，只需扭开顶部钢筋混凝土盖板固定螺栓，把振动棒从仓内取出即可，大大提高了检修安全性；当1个振动棒出现故障时，其他振动棒可以继续工作，确保了振动助流的连续性。

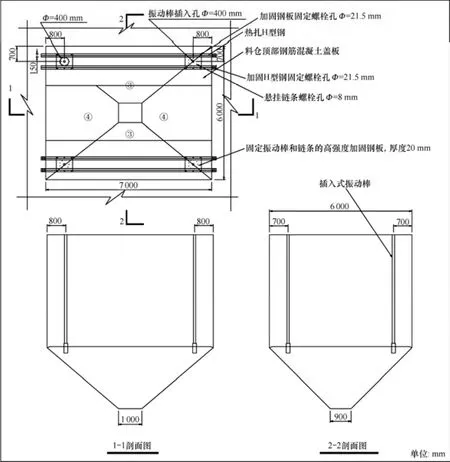
图4 仓内悬垂式振动主流器安装图Fig. 4 Installation plans for vertical vibration flow-aiding device

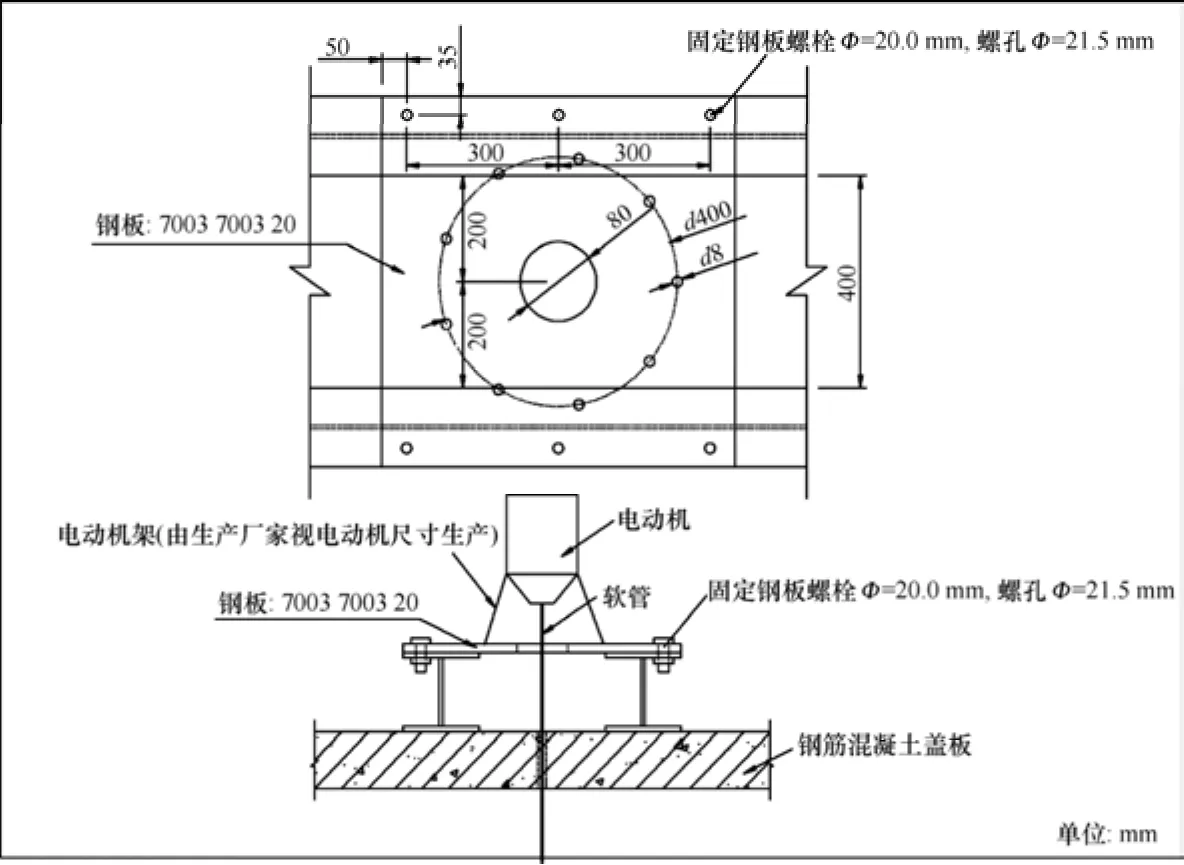
图5 固定钢板安装示意图Fig. 5 Steel plate installation diagram

表1 振动器参数Table 1 Vibrator parameters

据室内实验结果，仓壁摩擦因素对矿石流动性影响也很大。为了充分发挥仓内悬垂式振动助流器助流作用，可以考虑在仓体漏斗部分安装超高相对分子质量聚乙烯辅助衬板，降低漏斗部分的摩擦力。安装时，充分利用仓内原有钢轨结构，将聚乙烯板材安装在相邻钢轨的缝隙中，形成钢轨与高分子材料的复合板材，增加板材抗冲击性能。聚乙烯板材与钢轨间隔安装效果如图7所示。

图6 抗拉耐磨链条固定示意图Fig. 6 Tensile wear resistant chain fixed diagram

图7 超高相对分子质量聚乙烯复合板材安装效果Fig. 7 Installation plans for ultra-high molecular weight polyethylene composite sheet

4 助流效果PFC2D模拟

为验证仓内悬垂式振动助流器结合超高分子量聚乙烯复合板材的助流效果，本文采用离散元软件PFC2D对底部放矿和侧面放矿效果分别进行模拟[17]。模型采用PFC2D自带的fish语言编辑，振动器安装在矿粒最容易黏仓的死角部位，模拟分为有振动器和无振动器2种情况。材料参数和料仓尺寸不变，振动频率为70 Hz，振幅为1.2 mm。振动器位于仓内直墙与漏斗结合处(图8)，在模拟中提供振动能，破坏模型仓死角处形成的拱基，确保颗粒向漏斗口运动。超高分子量聚乙烯复合板材通过降低模型仓壁材料摩擦因素来实现助流。

由图8可见：加入振动后，颗粒的流动性得到极大改善，只需要运算20万步，仓筒部分的颗粒就差不多放完(见图8(b)和8(d))，并且仓口处颗粒流速很快，仓壁内颗粒迅速朝仓口汇集，可见在振动作用下，仓内颗粒的运动得到极大优化，能够避免死角处颗粒的堆积问题。在PFC2D模拟中，沿仓壁布置压力监测点，发现在仓内死角安装模拟振动器后，仓内壁的动态侧压力大大减小(见图9)，且比较均匀，动态侧压力的优化有利于提高仓体使用寿命，降低检修频率。PFC2D数值模拟结果表明：采用仓内悬垂式振动助流器具有一定可行性。

图8 放矿效果对比Fig. 8 Ore discharge effect contrast

图9 动态侧压力对比Fig. 9 Dynamic lateral pressure contrast

5 振动助流工业试验

PFC2D数值模拟结果表明仓内悬垂式振动助流器具有很好的助流效果。为了验证助流器的实用性，选择洛阳铝矿破碎站其中1个底部放矿矿仓进行工业试验，振动器安装在矿石流动性最差的死角。为了增加放矿难度，采用边装矿边加水的方式，使矿石中水的质量分数分布均匀，同时，水可以从料仓底部的闸门流出，装满矿石并贮存24 h以上，确保仓底部不会聚集多余水分，使矿石粉末在仓内充分黏结，从而增加矿石放出难度。

放矿时首先采用重力放矿，充分发挥超高分子量聚乙烯复合板材摩擦因数小的优点，当重力放矿停止后再开动振动器进行振动放矿，这样既降低振动器的耗损，又减少电耗。现场工业试验结果表明：矿石在振动助流条件下，助流效果十分明显，矿石放出率达到95%以上，安全系数达100%[17]。图10所示为矿石放出前与放出后的效果。底部放矿现场工业实验结果表明：仓内悬垂式振动助流器在矿仓放矿中的应用具有重要意义。

图10 矿石放出前和放出后效果Fig. 10 Effect before and after discharge

6 结论

(1) 水的质量分数和仓壁摩擦因素对矿石流动性影响很大，是引起仓内矿石黏仓、起拱、卡斗的重要原因。当水的质量分数从8.2%增加到10.8%时，矿石流动性急剧下降；仓壁摩擦因素增大导致拱角承载力增加，破拱的难度加大。尤其对于矿石流动性差的死角处，容易残留大量矿石，导致矿仓有效容积减小。

(2) 在仓内死角安装振动器后，颗粒很快从漏斗流出，证明仓内振动助流能克服底部振动助流的缺点，振动波能够在仓内上部有效传播，使仓内矿石流动性得到优化；同时，仓内壁的动态侧压力也大大减小，且比较均匀，有利于提高仓体的使用寿命。

(3) 仓内悬垂式振动助流器与超高分子量聚乙烯辅助板材相结合，具有很好的助流效果，矿石放出率达95%以上，安全系数达100%。

[1]Anand A, Curtis J S, Wassgren C R, et al. Segregation of cohesive granular materials during discharge from a rectangular hopper[J]. Granular Matter, 2010, 12(2): 193−200.

[2]Ananda A. Predicting discharge dynamics from a rectangular hopper using the discrete element method (DEM)[J]. Chemical Engineering Science, 2008, 63(24): 5821−5830.

[3]李海旺, 刘静, 树学峰. 裤型漏斗型钢贮煤仓散料压力分布研究[J]. 工程力学, 2010, 27(6): 140−146.LI Haiwang, LIU Jing, SHU Xuefeng. Research on the distribution of granular coal pressure on the wall of a special silo with trouser-shape funnel[J]. Engineering Mechanics, 2010,27(6): 140−146.

[4]郑利娇, 郭晓镭, 肖为国, 等. 粉煤料仓下料稳定性实验[J].华东理工大学学报(自然科学版), 2007, 33(3): 359−364.ZHENG Lijiao, GUO Xiaolei, XIAO Weiguo, et al. Discharge stability of pulverized coal from bunker[J]. Journal of East China University of Science and Technology (Natural Science Edition),2007, 33(3): 359−364.

[5]肖国先. 料仓内散体流动的数值模拟研究[D]. 南京: 南京工业大学材料科学与工程学院, 2004: 29−46.XIAO Guoxian. Numerical simulation study upon granular materials flow in silos[D]. Nanjing: Nanjing University of Technology. College of Materials Science and Engineering, 2004:29−46.

[6]陈汝超, 陈晓平, 蔡佳莹, 等. 补气料仓中宽筛分粒煤的下料特性[J]. 化工学报, 2011, 62(6): 359−364.CHEN Ruchao, CHEN Xiaoping, CAI Jiaying, et al. Flow characteristics of granular coal in aeration silo[J]. Journal of China Coal Society, 2011, 62(6): 359−364.

[7]秦雯, 沙爱民, 胡倩. 混合料贮料仓离析现象试验研究[J]. 岩土力学, 2009, 30(增 1): 99−102.QIN Wen, SHA Aimin, HU Qian. Study of segregation phenomenon of mixture storage hopper[J]. Rock and Soil Mechanics, 2009, 30(S1): 99−102.

[8]肖国先, 徐德龙, 陈延信, 等. 料仓中仓型改流体作用的数值模拟[J]. 计算机与应用化学, 2005, 22(7): 500−504.XIAO Guoxian, XU Delong, CHEN Yanxin, et al. Numerical simulation study on the granular materials discharged from a silo with the Placement of cone-in-cone insert[J]. Computers and Applied Chemistry, 2005, 22(7): 500−504.

[9]徐泳, Kafui K D, Thornton C. 用颗粒离散元法模拟料仓卸料过程[J]. 农业工程学报, 1999, 15(3): 65−69.XU Yong, Kafui K D, Thornton C. Discharge simulations with different particulate properties using the distinct element method[J]. Transactions of the Chinese Society of Agricultural Engineering, 1999, 15(3): 65−69.

[10]解本铭, 朱晨, 崔大妍. 料仓压力的理论分析和实验研究[J].辽宁工程技术大学学报, 2007, 26(2): 276−277.XIE Benming, ZHU Chen, CUI Dayan. Theoretical analysis and experimental study on pressure of silo[J]. Journal of Liaoning Technical University, 2007, 26(2): 276−277.

[11]李志, 夏国涛, 肖国先, 等. 料仓中湿颗粒流动规律的数值仿真与试验研究[J]. 海南大学学报(自然科学版), 2004, 22(1):23−27.LI Zhi, XIA Guotao, XIAO Guoxian, et al. The numerical simulation and experiment research of wet particles flow in a hopper[J]. Journal of Hainan University (Natural Science), 2004,22(1): 23−27.

[12]陈汝超, 陈晓平, 蔡佳莹, 等. 粒煤在补气料仓中的下料特性[J]. 煤炭学报, 2011, 36(2): 331−335.CHEN Ruchao, CHEN Xiaoping, CAI Jiaying. Flow characteristics of granular coal in aeration silo[J]. Journal of China Coal Society, 2011, 36(2): 331−335.

[13]王乾. 基于双质体振动的主动活化料仓系统理论及实验研究[D]. 北京: 中国矿业大学机电与信息工程学院, 2011: 8−10.WANG Qian. Study on theory and experiment of initiative activating bunker system based on two mass vibration[D].Beijing: China University of Mining and Technology. School of Mechanical Electronic ＆ Information Engineering, 2011: 8−10.

[14]吴爱祥, 孙业志, 刘湘平. 散体动力学理论及其应用[M]. 北京: 冶金工业出版社, 2002: 236−242.WU Aixiang, SUN Yezhi, LIU Xiangping. Theory and application of granular dynamics[M]. Beijing: Metallurgical Industry Press, 2002: 236−242.

[15]王昌汉. 放矿学[M]. 北京: 冶金工业出版社, 1982: 29−30.WANG Changhan. Ore discharge science[M]. Beijing:Metallurgical Industry Press, 1982: 29−30.

[16]刘兴国. 放矿理论基础[M]. 北京: 冶金工业出版社, 1995:118−122.LIU Xingguo. Ore discharge basic theory[M]. Beijing:Metallurgical Industry Press, 1995: 118−122.

[17]张春阳. 散体矿岩移动规律模拟及高粘矿岩助流研究[D]. 长沙: 中南大学资源与安全工程学院, 2009: 42−72.ZHANG Chunyang. Ore particle flow regularity numerical simulation and high viscosity bauxite flow-aiding research[D].Changsha: Central South University. School of Resources and Safety Engineering, 2009: 42−72.