大型水压机操纵系统瞬变负载的控制策略

杨俊，谭建平，陈玲，舒招强

(中南大学 机电工程学院，湖南 长沙，410083)

大型水压机传统的水路开启方式是通过人工操纵大扳把机构控制水阀阀芯的启闭，实现水压机的速度与位置控制。这种控制方式的效率和精度都很低，严重影响了产品的质量和生产效率。随着现代电液控制技术的发展，将新技术引入传统水压机极大地提高了水压机的效率与控制精度。通过设计一套液压操纵系统，将传统的大扳由“水控水”改造成一套“油控水”的系统，通过控制油缸的位置来控制水阀阀芯的启闭，这种方式在现代水压机的改造上得到了广泛应用[1−2]。由于水阀阀芯在开启初始阶段，开启力很大且存在不确定性，可以近似认为是一种瞬变的负载。传统的控制方式不能满足阀芯的高精度控制。郭玉玺等[3]采用液压位置伺服系统控制主分配器，系统的跟随效果不好，精度较低，存在着稳态误差。黄长征等[4]对300 MN模锻水压机利用 PID−H∞控制策略较好地解决了瞬变控制的问题，但是采用鲁棒控制会降低跟随性能，且极点的配置对系统模型要求比较精确，不利于复杂环境的现场应用。大型水压机操纵系统实际是一套液压位置伺服系统，针对液压系统的参数的不确定性与非线性和外部干扰的复杂性，国内外学者进行了深入研究，提出了很多新型的控制策略，但是由于算法的复杂性和工业现场的环境问题，现阶段很多控制策略在工程上实现有很大的难度，并且效果不是很显著[5−10]。精确线性化是基于微分几何的非线性控制策略，在对大扰动和大给定量的情况的非线性系统有较好的控制特性[11]，且对系统参数的变化具有很强的稳定性[12]，由于精确线性化是将非线性问题转化成简单的线性问题处理，控制器的设计与参数的调整简单易理解，所以，在液压控制上得到了广泛应用。但是，精确线性方法对外负载的动态干扰有较大的动态超调量，不适合水压机的外负载复杂性的特点。而滑模变结构控制使系统在一定的特性下沿规定的状态轨迹进行小幅度、高频率的上下运动，能有效地解决系统参数时变，时滞和瞬变等问题，在液压系统的位置、速度和力控制中得到了广泛应用[13−15]。本文作者基于精确线性化和变结构控制提出一种针对液压系统存在巨大瞬变负载的复合控制策略，利用精确线性化提高液压系统稳态特性，利用变结构控制策略补偿瞬变负载干扰。该策略具有设计简单、参数调整方便的特点，将控制策略应用于大型水压机操纵系统，验证系统的鲁棒性和控制精度问题。

1 操纵系统的构成

大型水压机的操纵系统示意图如图1所示，包括液压传动部分、控制部分、上位机部分及一套阀芯开启装置。

液压传动部分包括泵站及其附属设施，为操纵系统的工作提供动力；控制部分由 PLC及附属设备组成，包括接受上位机控制指令，为比例阀流量阀给定控制信息；上位机部分包括上位机及操作手柄等，主要提供控制的参考指令和系统状态监控；阀芯开启装置由齿轮齿条，凸轮顶杆机构组成，将液压缸的位移转变成阀芯的位移，实现水压机的启闭过程。

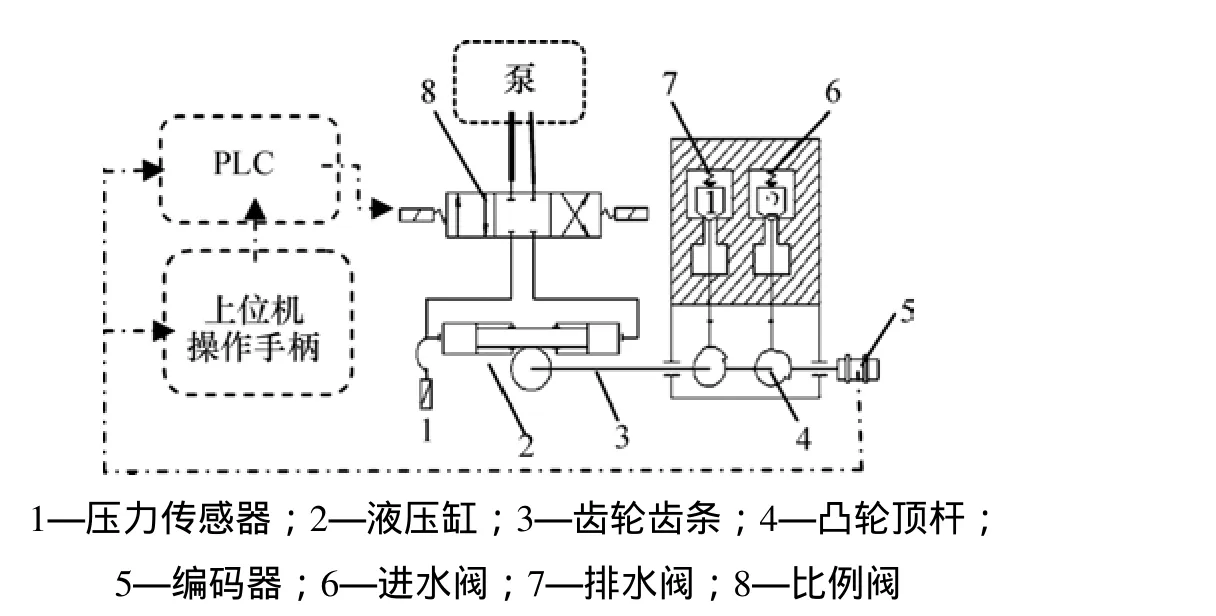
图1 操纵系统原理图Fig. 1 Schematic diagram of operation system

控制过程为：通过编码器对凸轮的转角实现反馈，比较手柄转角与凸轮转角的差值，实现操作系统闭环控制。从而实现对水路分配器系统的方向和流量的精确控制，为了提高系统控制的精度和稳定性，可以在系统中设计一些控制策略。

2 操作系统负载特点

大型水压机一般为泵−蓄势器的传动方式，通过主阀芯的开启与关闭实现水压机的动作过程。进、排水阀的结构大致相同，属于提阀类，一般采用平衡式带泄压阀的结构，在主阀内装有直径较小的先导泄压阀。开启过程为：通过操纵系统作用于凸轮，将阀杆向上顶起，首先泄压阀泄压，主阀上腔的压力迅速减小，主阀开启力减小，然后打开主阀，主阀打开后，继续开启，阀芯开口度增大，流量增大。

由于水压机工作的压力很高，一般为30 MPa以上，因此，即使采用泄压阀后，阀芯的开启力也是巨大的。文献[16]基于流体动力学理论，通过建立单个提阀的数学模型并对大型水压机开启力进行分析，得到了水压机的阀芯开启力。阀芯开启力如图2所示。从图2可见：在开始阶段开启力较小，之后突然增大，然后迅速减少。在上位机中对操纵系统液压油站的压力进行监控与分析，得到水压机正常工作阶段在某段时间内的压力曲线，如图3所示。根据图3可知：油压曲线是一系列的突变曲线，表明工作过程中油压是突然变化的，也证明了负载是一系列的瞬变载荷。

由以上的分析可知：系统负载的特点是开启的瞬间需要的开启力很大，然后突然减小，载荷存在瞬变。由于主分配器上集成多个阀芯，一次工作需要开启多个阀芯，所以，负载是一系列的瞬变载荷叠加而成。

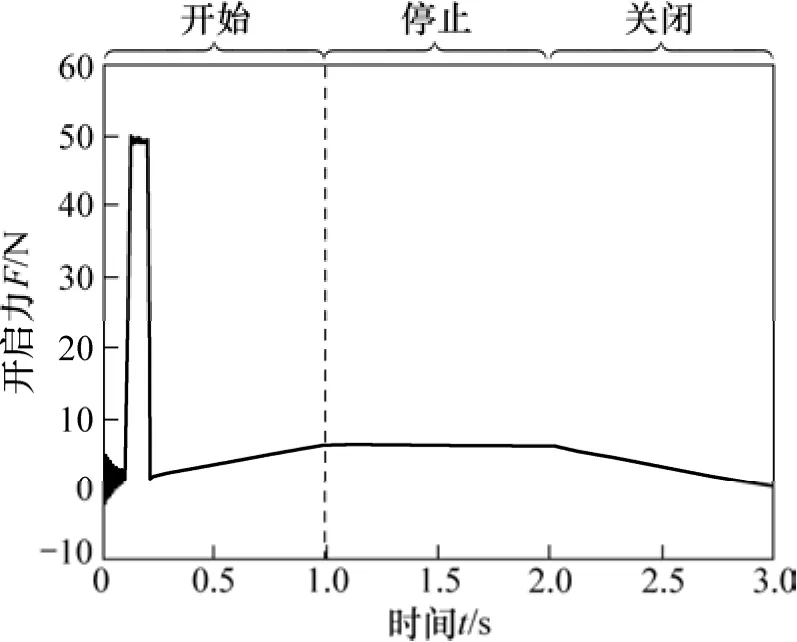
图2 阀芯开启力Fig. 2 Force of valve open

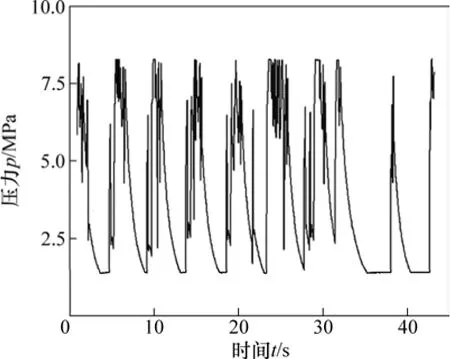
图3 油缸的压力Fig. 3 Pressure of cylinder

3 瞬变负载下液压控制策略

3.1 系统的数学模型

大型水压机操纵系统是一个典型的仿射非线性系统，即系统输出对状态量表现为非线性，对控制量表现为线性，又由于系统的惯性负载起主导作用，忽略其弹性负载，状态空间表达式可写成[17−18]：

其中：

y,和分别为液压缸的位移、速度和加速度；pA和pB分别为两腔的压力；VA和VB分别为包含管道的液压油体积；FL和Ff分别为缸的负载力和摩擦力；AA和AB分别为腔的作用面积；m，E和Ct分别为负载质量、液压油的体积模量和液压缸泄露系数，为常量；QN和pN分别是比例阀的最大的流量和额定压力；p0和pT分别是液压泵的供油压力和油箱压力；xv为阀芯的位移。

基于式(1)分析系统特性满足一般的工业现场分析要求，但是工业现场的环境复杂性和不确定性导致液压系统的参数是不确定的或者是未知的，所以只能得到不精确的系统的动态特性，如果全面考虑这些因素的影响，控制器将变得相当复杂，甚至会导致系统不稳定。

为了让高级控制策略适用于工业现场，需要对原始模型进行简化，忽略一些次要因素如泄漏，并对一些参数进行估计，以便控制器的设计与调整，可得不精确的液压系统模型。

3.2 控制策略

3.2.1 精确线性化控制器

精确线性化是基于微分几何的方法非线性控制方法，在工业控制上取得了广泛应用，精确线性化的方法是首先求得系统(9)的相对阶为 3。选择式(12)的微分同胚变换。

其中：Lfh(x)表示h(x)沿f方向的李导数。函数的i阶李导数为：。

得到新坐标系中的系统状态方程：

其中：

选择输入输出线性化控制

其中：xd为期望的位置；e=xd−x为位置的误差。

3.2.2 滑模变结构干扰补偿器

由于式(17)中 3个参数选择比较困难，且参数的值极大的影响了瞬变载荷对系统的影响，为了提高系统的瞬态与稳态特性，将滑模变结构控制策略引入到参数的选择中来，由于滑模控制是一种开关量控制，可以在瞬变载荷的开始瞬间可以提供较大的控制电量，平衡系统的瞬态负载影响。

定义滑动模态平面：

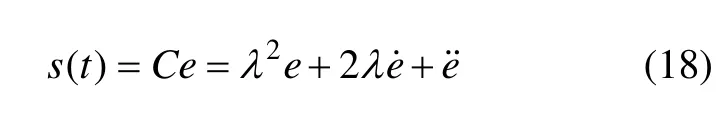
式中：λ为正常数。为了将精确线性化控制器和滑模变结构补偿器中系数联系起来，设定λ2=k，2λ=k2，k3=1。

由于阀芯的开启力是一个有限值，干扰有上界，即FL＜D。当系统存在瞬变负载时，设计一个控制器使

按照等效函数切换控制，设计控制律。

式中：k=D+η为控制增益；D为补偿突变的负载参数；η为控制切换的速度的参数。

在式(19)中，由于符号函数sgn(s)的存在，上述控制律为不连续控制律，不连续函数的引入将会造成系统的颤振。将符号函数用以下近似可导函数式代替：

则系统最终的控制律为

3.2.3 系统鲁棒性分析

选择式(21)线性化近似变结构控制律作用于式(9)的控制系统，对其进行鲁棒性分析。

取李亚普洛夫函数

则

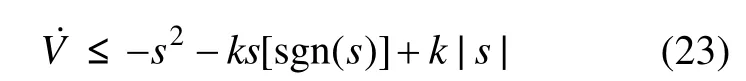
4 仿真分析与现场应用

4.1 仿真分析

为验证控制策略在瞬变负载控制中的可行性，利用Matlab-Simulink进行建模分析。其中流量阀的模型按照现场使用情况，选用意大利阿托斯公司的比例流量阀，阀参数产品说明书上选取。其他参数参照大型水压机操纵系统的参数，如表1所示。

液压系统的控制原理如图4所示，由参考输入信号、控制器、液压传动及反馈部分组成。

表1 液压系统参数表Table 1 Parameters of hydraulic system

图4 复合控制原理图Fig. 4 Schematic diagram of I-Olin with SVC

现场是通过控制操作手柄控制液压缸的位移，按照工作人员的操作习惯，可以认为是对系统给定一个阶跃输入，即手柄一下转动到给定位置。

由于液压缸活塞杆的位移和凸轮的转角存在比例关系，为了方便，可以通过分析活塞杆的动态特性来分析凸轮的动态特性。图5和图6所示为模拟液压缸移动0.05 m时系统的响应情况。其中仿真时间2 s，采用ode15算法，并在时间t=0.5～0.6 s时加入瞬变负载FL=20 kN。仿真比较PID、精确线性化和复合控制策略的动态特性。

图5 控制信号比较Fig. 5 Comparison of input signal of controllers

图6 不同控制策略的动态响应Fig. 6 Dynamic response of system under different control strategy

图5 所示为各控制策略的电流输入情况，按实际情况，比例阀的额定电流为0.4 A，所以，设定电流的上限为0.4 A。由图5可知：精确线性化对系统很敏感，控制电流的波动很大。在载荷变化情况下，电流输出产生瞬变；复合控制策略变化次之。由于加入了近似可导函数，其控制没有明显的抖动，控制电流比较平稳。PID控制策略对系统的载荷变化最不敏感，其控制电流比较平稳，同时也表明了PID控制策略系统参数变化不敏感。

由图6可知：对比3条动态响应曲线， PID控制系统存在着超调，超调量为20%；系统响应时间约为0.2 s；精确线性化控制策略曲线，系统无超调，响应时间约为0.2 s；变结构与精确线性化的复合策略系统无超调，系统响应时间比仅仅采用精确线性化方法长一点。由上分析，在响应的速度方面，PID响应时间最长，精确线性化和复合控制区别不大，但是，PID控制策略的超调量较大，影响了系统的瞬态特性。

在系统的稳态输出方面，PID控制有一定的稳态误差，达到4.5%。精确线性化和复合控制策略基本上都没有稳态误差，说明PID控制策略不能解决系统的追踪问题。

在对瞬变负载的抗干扰能力方面，PID控制策略较好，系统的位移波动幅度最小，仅为 4%；精确线性化方法，波动达到30%；复合控制策略，波动达到8%；显然，对于瞬变的载荷影响，PID控制策略较稳定，复合控制策略次之，精确线性化最差，也说明精确线性化方法对系统变化敏感。

综合以上分析，采用复合控制策略，响应时间较短，无稳态误差，对瞬变载荷不是很敏感，能有效解决瞬变负载和精确追踪问题，表明基于精确线性化和变结构控制的复合策略的综合性能较好。

4.2 现场实验

针对西南铝300 MN模锻水压机液压系统，利用德国 PVS58I旋转编码器转角测量凸轮的转角，速度与加速度采用对转角的前向差分和速度差分方法获得；两腔的压力采用WS系列电容式压力传感器检测，手柄的转角直接输入到上位机，并与编码器测量的转角进行比较；上位机系统采用 AWS8248工控机，软件采用WinCC；控制处理器采用PLC，在上位机上对过程和结果进行动态显示。

现场测的凸轮转角与操作手柄的响应曲线如图 7所示。凸轮转动角度基本能追踪手柄转动的角度，但是凸轮转角有一段时间的延迟，约为0.6 s，比仿真时间长。

图7 凸轮与手柄转角Fig. 7 Angle of cam and operation handle

在稳态误差的消除方面，实验结果表明：复合控制的稳态误差约 8°，最大相对误差为 4%，该误差包含了机械系统的误差和环境因素的影响误差，具体问题需要进一步的研究。

由以上分析可得：系统的实际的响应时间大于仿真时间，且位置追踪存在一定的稳态误差，与理论结果有一定的差距。这是现场的环境变化、液压系统的不确定性和机械机构的磨损、间隙等原因所致，也是下一步研究的重点。

5 结论

(1) 建立大型水压机液压操纵系统的数学模型并进行了合理简化。通过将瞬变负载当外部干扰的处理方式，提出适用于工业现场的基于精确线性化和变结构控制的复合控制策略。

(2) 从对瞬变负载控制的稳定性方面考虑，传统的PID控制策略最好，精确线性化控制策略最差，但是PID有稳态误差，会影响凸轮的转动精度。

(3) 基于精确线性化和变结构的复合控制策略比PID控制和精确线性化控制有更好的突变载荷抑制作用，系统稳态误差小，操纵系统的鲁棒性和控制精度得到了显著提高。

[1]姚静, 孔祥东, 单东升, 等. 50 MN自由锻造水压机电液伺服控制系统负载特性分析[J]. 机床与液压, 2006(8): 101−104.YAO Jing, KONG Xiangdong, SHAN Dongsheng, et al. The electro-hydraulic servo control system load characteristic analysis of 50MN water press for free forging[J]. Machine Tool and Hydraulics, 2006(8): 101−104.

[2]谭建平, 黄长征, 刘彬, 等. 瞬变载荷下巨型水压机液压操作控制策略[J]. 机械工程学报, 2008, 44(11): 272−277.TAN Jianping, HUANG Changzheng, LIU Bing, et al. Control strategy of hydraulic operation system under the transient load in giant hydrulic press[J]. Chinese Journal of Mechanical Engineering, 2008, 44(11): 272−277.

[3]郭玉玺, 丁耀林, 罗上银. 大型热模锻水压机的电液伺服控制系统[J]. 锻压机械, 2002(4): 13−17.GUO Yuxi, DING Yaolin, LUO Shangyin. Electro–hydraulic servo-control system for large hydraulic press for hot die forging[J]. Metal Forging Machinery, 2002(4): 13−17.

[4]黄长征. 300 MN模锻水压机动梁驱动速度响应特性及速度控制研究[D]. 长沙: 中南大学机电工程学院, 2007: 58−114.HUANG Changzheng. Research on dynamic response characteristic and speed control of moving beam drive system for 300 MN die forging hydraulic press[D]. Changsha: Central South University. School of Mechanical and Electrical Engineering, 2007: 58−114.

[5]Mark K, Nariman S．On quantitative feed back design for robust position control of hydraulic actuators[J]. Control Engineering Practice, 2010(18): 289−299.

[6]Vladimir M, Zeljko S, Mario E. Robust position control synthesis of an electro-hydraulic servo system[J]. Isa Transactions, 2010(49): 535−543.

[7]Ali S, Hadi S, Kamyar G, et al. Identification and real-time position control of a servo-hydraulic rotary actuator by means of a neurobiologically motivated algorithm[J]. Isa Transactions,2012(51): 208−219.

[8]Loukianov G, Sanchez E, Lizalde C. Force tracking neural block control for an electro-hydraulic actuator via second-order sliding mode[J]. Int J Robust Nonlin, 2008, 18(3): 319−332.

[9]杨军宏, 李圣怡, 戴一帆. 阀控非对称缸非线性系统高精度位置跟踪鲁棒控制研究[J]. 中国机械工程, 2007, 18(23):2801−2805.YANG Junhong, LI Shengyi, DAI Yifan. Research on high performance position tracking robust control strategy of a vave controled asymmetric nonlinear system[J]. China Mechanical Engineering, 2007, 18(23): 2801−2805.

[10]邵俊鹏, 王仲文, 李建英, 等．电液位置伺服系统的规则自校正模糊 PID 控制器[J]. 中南大学学报(自然科学版), 2010,41(3): 960−965.SHAO Junpeng, WANG Zhongwen, LI Jianying, et al. Rule self-tunning fuzzy-PID controller of electro–hydraulic position servo system[J]. Journal of Central South University (Science and Technology), 2010, 41(3): 960−965.

[11]李运华, 王孙安, 林廷析, 等. 液压伺服系统的非线性优化设计[J]. 机床与液压, 1994(5): 255−260.LI Yunhua, WANG Sunan, LIN Tingxi, et al. nonlinear control system optimization and design of hydraulic servo system[J].Machine Tool and Hydraulics, 1994(5): 255−260.

[12]Roger F, Atul K. Robust control design for a wheel loader using H∞ and feedback linearization based methods[J]. ISA Transactions, 2009(48): 312−320.

[13]胡剑波, 庄开宇. 高级变结构控制理论及应用[M]. 西安: 西北工业大学出版社, 2008: 19−43.HU Jianbo, ZHUANG Kaiyu. Theory and application of advanced sliding variable structure control[M]. Xi’an:Northwestern Polytechnical University Press, 2008: 19−43.

[14]GUAN Cheng, PAN Shuangxi. Adaptive sliding mode control of electro-hydraulic system with nonlinear unknown parameters[J].Control Engineering Practice, 2008, 16: 1275−1284.

[15]Liu Y, Handroos H. Sliding mode control for a class of hydraulic position servo[J]. Mechatronics, 1999, 9(1): 111−123.

[16]陈晖, 谭建平. 大型模锻水压机高压大流量水阀开启力特性[J]. 中南大学学报(自然科学版), 2012, 43(8): 2993−2999.CHEN Hui, TAN Jianping. Opening force characteristic of water valve with high pressure and large flow capacity in large die forging hydraulic press[J]. Journal of Central South University(Science and Technology), 2012, 43(8): 2993−2999.

[17]Komsta J, Oijen V, Antoszkiewicz P. Integral sliding mode compensator for load pressure control of die-cushion cylinder drive[J]. Control Engineering Practice, 2011(12): 1−11.

[18]王占林. 近代电气液压伺服控制[M]. 北京: 北京航空航天大学出版社, 2004: 16−50.WANG Zhanlin. Modern electronic hydraulic servo control[M].Beijing: Beihang University Press, 2004: 16−50.