农村水利管理的利益相关者博弈均衡分析——以浙江省为例<br/>

农村水利管理的利益相关者博弈均衡分析——以浙江省为例

2014-11-29张宁，华楠

杭州电子科技大学学报(社会科学版) 2014年6期

张宁，华楠

(杭州电子科技大学管理学院，浙江杭州310018)

我国自实行农业经营制度改革以来，农村水利工程主要实行以村委会为主的村集体直接管理模式，这也使得农村水利管理利益相关者的权责发生了很大的变化。本研究以浙江省农村水利为例，探讨与农村水利管理相关的多方利益主体之间的竞争和制衡关系，试图理清其间错综复杂的利益关系，目的在于建立符合地方特色的有效市场化管理模式，以便更好地促进农村水利建设与管理的可持续发展。本文从利益相关者综合制衡的角度出发，鉴于不同利益相关者的利益与权力具有差异性，采用利益相关者理论、利益分析工具和博弈均衡模型，分析各利益相关主体之间更为深层的利益关系与矛盾。旨在为农村水利市场化管理过程中利益激励和约束机制的提出创新的可能性，从而揭示浙江省农村水利建设与管理发展的内在动力，为其管理模式与激励机制的设计提供思路和参考价值。

一、农村水利市场中的利益相关者

美国学者米切尔(1997)曾提出利益相关者理论的两个核心问题，即认定谁是利益相关者(stakeholder identification)和利益相关者的特征(stake-holder salience)［1］。农村水利利益相关者是指在水利管理的整个过程中，任何可以影响其管理效率的群体或个人。本文通过查阅整理文献、对浙江省各地级市的实地调查及参考利益相关者理论文献，对浙江省农村水利的利益相关者作出了初步的总结，分为以下几种类型，如表1所示:

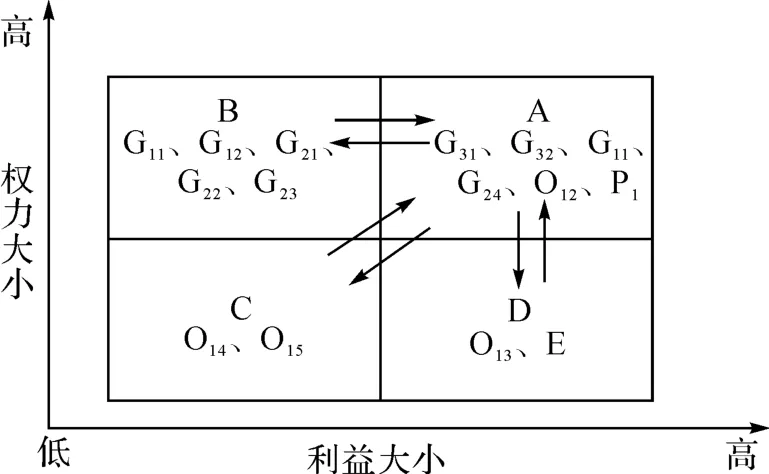
本文以浙江省为例证，运用米切尔提出的利益相关者的“双相”差异性和Mende-low 的利益相关者权利-利益矩阵(Stakeholder Mapping)［2－4］来进行相关分析，如图1所示。在此理论基础上将以上通过文献调查和实地调查列举出的浙江省农村水利管理中的15 个相关的利益相关者进行二维模块分析，如图2所示。其中横坐标表示浙江省农村水利对某利益相关者的利益影响的程度，纵坐标表示某相关主体在农村水利中所具有的权力大小。

根据实地调查访问的结果将15 个利益相关者较为合理的列于A、B、C、D 四个模块区中。其中:A区是最为关键的利益相关者，因为农村水利的管理好坏对他们自身利益影响较大，所以他们对水利的决策最感兴趣的同时也最有发言权，是最为关键的人群;B 区是权力大、兴趣小的利益相关者，他们主要是政府部门，所以其对农村水利的维护权力大，但农村水利管理的好坏对其切身利益影响不大;C 区是权力小且兴趣也小的利益相关者，这类群体一般情况下很少去关注农村水利的管理工作及其成效，所以相对而言他们付出的努力也是最小的;D 区是权力小但兴趣大的利益相关者，他们对农村水利的管理工作及其成效兴趣较大，利益相关程度也较大，但是却没有足够的权力去维护相应的利益。通过调研访问及专家意见可知社会团体在农村水利建设中的活跃度与农户、政府及其他集体相比较低，为了便于研究，本文优选出关键利益相关者中最主要的农户(P1)、村委会(G32)、水利站(G31)、乡政府(G24)等利益主体进行博弈分析，探讨他们共同参与水利管理之间的博弈均衡。

表1 农村水利市场管理中的利益相关者

图1 利益相关者权力-利益识别定位

2 农村水利管理的利益相关者分区图

二、农村水利市场利益主体参与现状调查

为了对浙江省农村水利利益相关者参与式水利管理做一个系统的了解，本文通过实地调研和统计年鉴查阅等方法，对浙江省农村水利设施管理状况及相关利益主体的参与情况进行了梳理。调查样本主要来自作者对浙江省诸暨市、温州市、湖州市等的13 个(乡)村、灌区的260 个农户的调查，其中地区以统计资料为主，农户以问卷调查为主，调查时间为2014年8月4日至11日，分三组，共计六人，调查共发放问卷260 份，回收有效问卷233 份，回收率为89.6%。在调查中课题组发现，农户对参与式水利管理的了解程度不高导致参与程度低下，在调查的农户中，仅有29.18%的农户表示对农村水利工程参与式管理比较了解，70.82%的农户表示从没参与过农村水利管理。不仅如此，通过数据整理还发现浙江省农村水利管理效率偏低，如图3、4。

由图3 可以看出，水利投资额的增加没有带动有效灌溉面积的增加。图4 也显示，政府及水利管理部门对水利管理工作缺乏指导，没有切实提高农户参与的积极性，从而导致地区水利管理劳动总投入降低，为此本文将进一步展开政府、水利管理部门及农户等利益主体之间的博弈均衡分析。

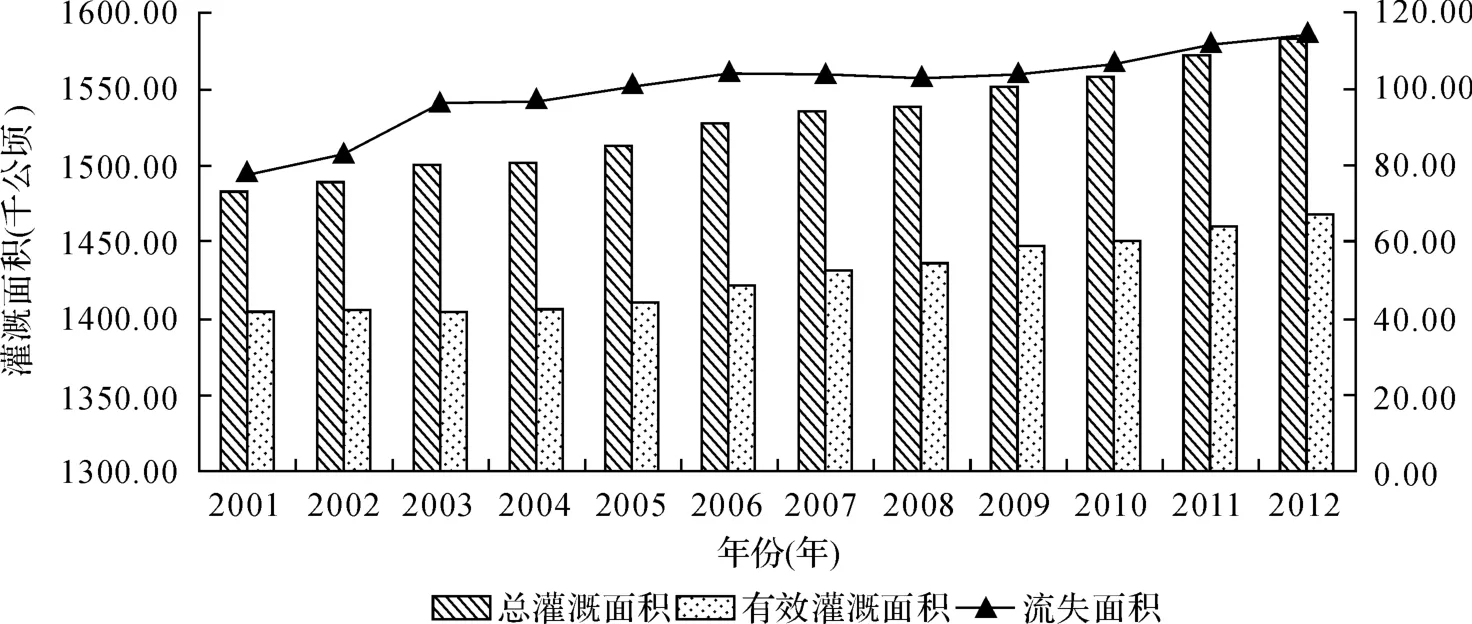
图3 2001—2012年浙江省有效灌溉面积变化

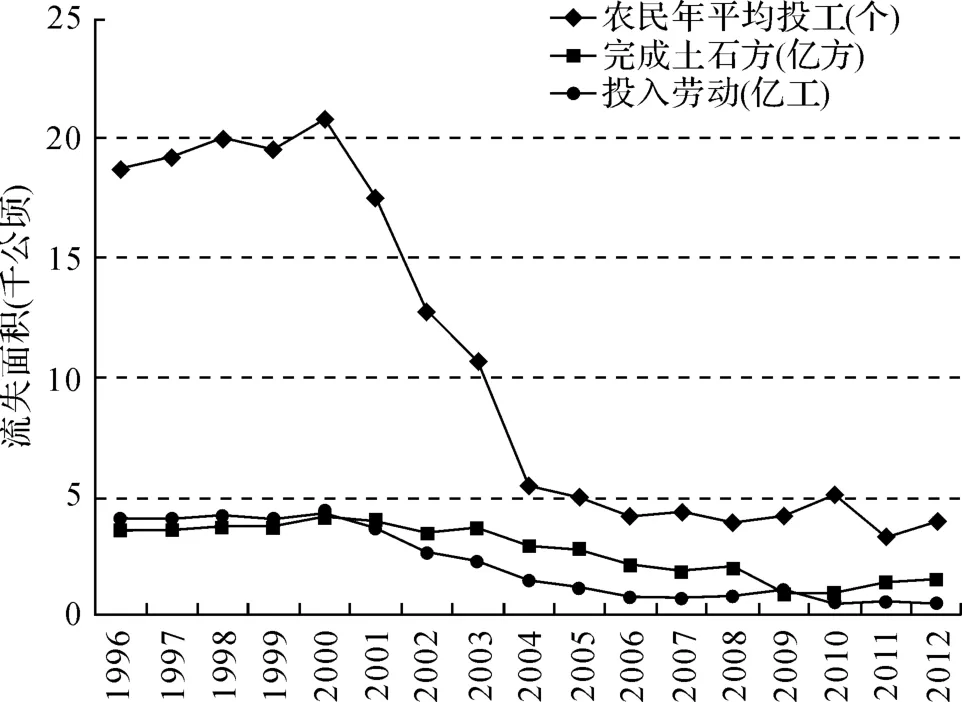
图4 1996—2012年浙江省农村水利建设劳动投入

三、水利管理中的利益相关者博弈均衡模型构建

根据调研及访问结果，对浙江省农村水利主要利益相关者及其行动空间做出归纳:乡政府的行动空间表现为是否有效监管;水利站的行动表现为是否有效监管;村委会行动表现为是否努力工作;农户的行动表现为是否参与管理。根据利益相关者的利益诉求，运用博弈均衡模型重点分析乡政府与水利站、水利站与村委会、村委会与农户、农户与农户之间的深层利益关系与矛盾。

(一)参数定义及变量说明

两两博弈模型中涉及到的变量及其代表符号纷繁复杂，为了便于分析，分别对乡政府、水利站、村委会和农户的相关参数进行了定义［5－7］，概括如表2。

(二)利益相关者的博弈均衡状态求解

自我国施行农村水利市场化政策之后，农村水利的建设主要归乡政府和水利站所有，其产权也属于乡政府或集体，管理的经费主要来自于水费的征收［8－9］，但是据对浙江省各地级市的调查发现，很多农村水利的维护和运营工作都没有充足的资金做后援，乡政府和水利站对水管人员的监管、考核工作举步维艰，导致了农村水利管理效益日益衰减。这主要是因为在缺乏有效激励和监管措施的情况下，各利益相关者都想获得自身利益最大化从而导致了博弈损益。

表2 博弈均衡模型中主要参数说明

1．乡政府与水利站之间的博弈分析

乡政府和水利站之间的搏弈损益如表3所示。

表3 水利站与乡镇府、村委会之间的博弈损益分析

由表3 可以看出乡政府的期望收益为［10］:

Et(p，α)=p［α(f－k2)+(1－α)(A－k2)］+(1－p)［αf+(1－α)*0］

乡政府要达到收益值最大，需Et(0，α)=Et(1，α)，此时α*=(A－k2)/A，这表明:当α＜α*时，水利站的监管力度较小，此时乡政府的最优决策是进行监管;当α＞α*时，水利站的监管力度较大，此时乡政府不进行监管就能获得期望收益;当α=α*时，水利站的监管力度恰到好处，此时乡政府监管与否对其期望收益都无影响。

同理，水利站的期望收益可以表示为:

E0(p，α)=α［p(－k3)+(1－α)(－k3)］+(1－α)［p(－A)+(1－p)*0］

水利站要达到收益值最大，需E0(p，0)=E0(p，1)，此时p*=k3/A，这表明:当p＜p*时，乡政府的监管力度较小，此时水利站进行决策才有获得期望收益的可能;当p＞p*时，乡政府的监管力度较大，此时水利站的最优决策是不进行监管;当p=p*时，水利站进行监管与否都对其期望收益没有影响。

所以，乡政府和水利站的纳什均衡为:(p*=k3/A，α*=(A－k2)/A)

即水利站和乡政府分别以α*=(A－k2)/A 和p*=k3/A 的概率进行监管时二者同时都可以获得最优收益。

由p*=k3/A 可知，乡政府的监管概率p*与水利站的监管成本k3成正比，即水利站的监管成本越大，为了不付出监管费用，其就越不想参与监管工作，所以乡政府对水利站的监管概率也就会越高;由α*=(A－k2)/A 可知，水利站的监管效率α*与乡政府的监管成本k2成反比，即乡政府的监管成本越高，其就越不想参与监管工作，那么可想而知在没有乡政府监督的情况下，水利站也不会自觉的进行监管，所以其监管概率也会降低;另外，对于水利站的监管效率α*来说，乡政府对水利站的行政处罚A 越大，α*就越大，即水利站进行监管的概率就越大;而乡政府的监管效率p*则与A 成反比，即乡政府对水利站不监管的惩罚越低，它就越有理由相信水利站不会尽心监管，所以乡政府对水利站的监管效率p*就必定会变大。因此提高A 与降低k2有利于增大水利站的监管概率，提高k3与降低A 有利于增大乡政府对水利站的监管效率。

2．村委会与水利站之间的博弈分析

由表3 可以看出村委会的期望收益为:

Ec(α，p0)=p0［α(T0－k4)+(1－α)(－k4)］+(1－p0)［α(t0－A0)+(1－α)t0］

当p0=0 和p0=1 时，村委会的期望收益分别是:Ec(α，0)=t0－αA0;Ec(α，1)=αT0－k4。当Ec(α，0)=Ec(α，1)时，村委会的期望收益达到最大，此时α*=(t0+k4)/(T0－A0)，表明当α＜α*时，水利站的监管程度较低，村委会将不会努力工作;当α＞α*时，水利站的监管程度较大，尚需要努力工作才能获得期望收益;当α=α*时，水利站的监管程度恰到好处，村委会努力工作与否对其期望收益都无影响。

同理，水利站的期望收益可以表示为:

E0(α，p0)=α［p0(－k3)+(1－p0)(－k3－E0+A0)］+(1－α)［P0* 0+(1－P0)(－E0)］

当α=0 和α=1 时，水利站的期望收益分别为:E0(0，p0)=E0p0－E0;E0(1，p0)=－k3－E0+A0+p0E0－p0A0。

当E0(0，p0)=E0(1，p0)时，水利站的期望受益最大，此时p0*=(A0－k3)/A0，这表明当时，村委会的努力程度较大，水利站不用进行监管就能获得期望收益;当时，村委会的努力程度恰到好处，水利站监管与否对其期望收益都无影响。

所以，村委会和水利站的纳什均衡为:

p0*=(A0－k3)/A0，α*=(t0+k4)/(T0－A0))

即村委会以p0*=(A0－k3)/A0的概率努力工作和水利站以α*=(t0+k4)/(T0－A0)的概率进行监管时二者同时都可以获得最优收益。

由p0*=(A0－k3)/A0可以看出:村委会选择工作的概率p0* 随着水利站对其的处罚A0的增大而增大。还可以看出:水利站进行监管的概率α*与p0* 呈负相关，即水利站监管成本k3越小，村委会就会觉得水利站更愿意进行监管，所以它选择努力工作的概率也就会越高。也就是说，k3减小和A0增大都有利于使村委会努力工作的概率增大。

3．农户甲与村委会之间的博弈分析

农户甲和村委会之间的博弈损益如表4所示。

由表4 可以看出农户甲的期望收益为:

Ev(p0，θ)=θ［p0(G+V－C0)+(1－p0)*0］+(1－θ)［p0(V－C0)+(1－p0)(－S)］时，村委会的努力程度较低，水利站需要加强监管;当

村委会的期望收益为:

Ec(p0，θ)=p0［θ(－k4)+(1－θ)(－k4－C)］+(1－p0)［θt0+(1－θ)*0］

另外，由θ*=(－k4－C)/(t0－C)可以看出，村委会不努力工作的投机利益t0和村委会努力工作的成本k4都与农户参与管理的概率θ*成反比，即若k4和t0都足够小，村委会不努力工作无利可图，努力工作又不需要付出较大成本，作为理性人他的最优策略必定是努力工作，那么在其努力监管的情况下，农户参与管理的概率θ*也会增大。综上所述，必须使村委会意识到不努力工作无利可图，且努力工作不需要付出太大成本的情况下，才能提高其努力工作的概率。失很大的情况下，为了减少损失他们就会比较积极地参与管理，那么村委会努力工作的概率

表4 农户甲与村委会、农户乙之间的博弈损益分析

4．农户甲与农户乙之间的博弈分析

由表4 可知，农户甲、乙参与管理的概率分别为θ，γ，则两农户进行多阶段完全信息重复博弈的行为如图5所示(图中“是”表示“参与”;“否”表示“不参与”)。

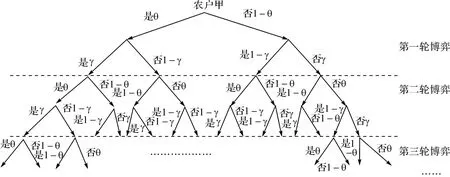
图5 农户甲、乙重复博弈的博弈过程

由图5 可以看出在第n 轮博弈中，农户甲有22n－1 种策略，农户乙有22n 种策略，以此可以推出甲、乙之间就会有无数种行为组合，而每一种行为组合都会成为一种策略［11－12］。

为了便于分析，针对农户甲、乙参与管理的策略组合，我们选取最具有代表性的四种进行讨论，即策略一:甲、乙都参与;策略二:甲参与、乙不参与;策略三:甲不参与、乙参与;策略四:甲、乙都不参与。

策略一:当农户甲总是参与，农户乙也总是参与时，农户甲的收益为:

(R－c)θγ+(R－c)θ2γ2+(R－c)θ3γ3+…+(R－c)θnγn=(R－c)θγ/(1－θγ)

农户乙的收益为:(R－c)θγ/(1－θγ)

策略二:当农户甲总是参与，农户乙总是不参与时，农户甲的收益为

(R－2c)θ(1－γ)+(R－2c)θ(1－γ)2(1－θ)+…+(R－2c)θ(1－γ)n(1－θ)n－1

农户乙的收益为:xθ(1－γ)/［1－(1－θ)(1－γ)］

策略三:当农户甲总是不参与，农户乙总是参与时，农户甲的收益为

x(1－θ)(1－γ)+x(1－θ)2(1－γ)2+…+x(1－θ)n(1－γ)n+…=x(1－θ)(1－γ)/［1－(1－θ)(1－γ)］

农户乙的收益为:(R－2c)(1－θ)(1－γ)/［1－(1－θ)(1－γ)］

策略四:当农户甲总是不参与，农户乙总是不参与时，农户甲的收益为:

y(1－θ)γ+y(1－θ)θγ2+…+y(1－θ)θn－1γn+…=yγ(1－θ)/(1－θ－γ)

农户乙的收益为:yγ(1－θ)/(1－θγ)

依据以上四种具有代表性的策略分析结果，可以清楚的知道农户甲、乙在各种策略选择下的期望收益，我们可以把农户甲和农户乙看作是同质的，所以可以假设θ=γ，分别取θ=γ=0.2、0.5、0.8、0.9四个数值，同时为了计算方便，假设R=5，c=2，x=5，y=2，结果如表5所示:

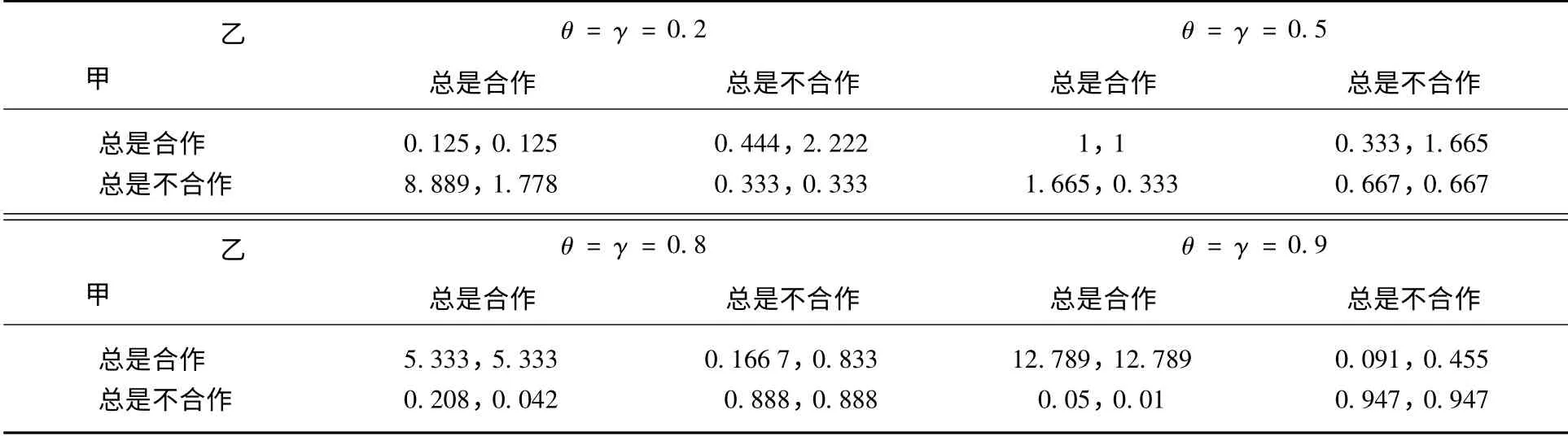
表5 不同合作意愿下农户甲、乙进行重复博弈的期望收益

结果显示，当θ=γ=0．2 时，农户甲乙的博弈不存在纳什均衡;当θ=γ=0．5 时，即农户甲和乙选择参与合作和不合作的概率各占二分之一时，双方的最佳选择是总是不合作;当θ=γ=0．8 时，双方最优策略是总是合作，并且其收益明显大于其它三种策略。当θ=γ=0．9 时，即双方会有很大的合作愿望，总是合作的收益也远远大于其他三种策略，并且此时的收益值较之θ=γ=0．8 也有较大提高。