考虑气相动态变化的泡沫油数值模拟研究

张艳玉，崔国亮，孙晓飞，段学苇，胡文涛

（1.中国石油大学（华东）石油工程学院，山东青岛266580；2.中海油能源发展工程技术分公司，天津300452）

出砂冷采稠油油藏具有较高的采收率、采油速度和较低的生产气油比，泡沫油是导致上述现象的重要原因［1］。泡沫油形成的动态过程主要涉及气相成核、成长以及气泡聚并与连通，气泡生长过程复杂，一方面受过饱和压力影响，另一方面随时间变化而变化［2］。前人针对超稠油非常规溶解气驱现象提出了系列数学模型［3-5］，包括拟泡点模型、分流量模型、粘度降低模型及改进的溶解气驱模型，但这些模型均不能完全表征泡沫油机理，对泡沫油的生产预测具有较大的局限性。为了准确描述稠油油藏泡沫油的渗流特征，在考虑压力对过饱和度影响、时间对非平衡参数影响以及气相变化对泡沫油参数影响的基础上，建立泡沫油动态数学模型，并结合泡沫油压力衰竭实验研究泡沫油的渗流特征。

1 稠油溶解气驱中的泡沫油机理

地层压力低于泡点压力后会产生过饱和现象，促使原油中的溶解气逐步分离产生逸出气，随着开发时间的变化和压力的进一步降低，一部分逸出气形成离散气伴随油相一起运移。这些含有离散微气泡的油气混合体系即为泡沫油，诸多离散微气泡的润滑作用可有效降低泡沫油粘度，微气泡的膨胀作用可以维持地层压力，同时降低气相流度和生产气油比。离散微气泡随时间的延长逐渐变大，最终离散气聚并形成连续的自由气，油藏中出现泡沫油和自由气两相渗流现象［6］。

泡沫油中的溶解气和离散气具有明显的相边界，故将二者定义为独立的相，即溶解气相和离散气相［7-8］。过饱和导致溶解气从油相中分离，过饱和现象包括热力学平衡和热力学非平衡2部分，分别与压力和时间相关，并分别用气液平衡常数和气相衰竭系数来表征。泡沫油中离散气的形成和聚并也与压力和时间有关，是压力和时间的幂函数，可利用气泡生长指数来表征气泡的生长过程。

2 泡沫油动态数学模型

2.1 模型假设

针对泡沫油的油气组成及其在多孔介质中的渗流特性，假设如下：①在渗流过程中，泡沫油以油相、溶解气相和离散气相3种形式存在，且离散气相分散在油相中并与其一起运移；②当油藏压力低于泡点压力时，溶解气逸出，由于原油粘度较大，逸出的溶解气以小气泡的形式分散在油相中形成泡沫油，随着压力的进一步降低或者时间的延长，小气泡生长、聚并形成自由气；③气相（自由气）和含有分散气泡的油相（泡沫油）在渗流过程中满足达西定律；④由于气泡尺寸微小，忽略毛管压力的影响。

2.2 模型建立

针对模型假设条件和质量守恒原理，建立了泡沫油中的油相、溶解气相、离散气相和自由气相4组分数学模型，其质量守恒方程分别为

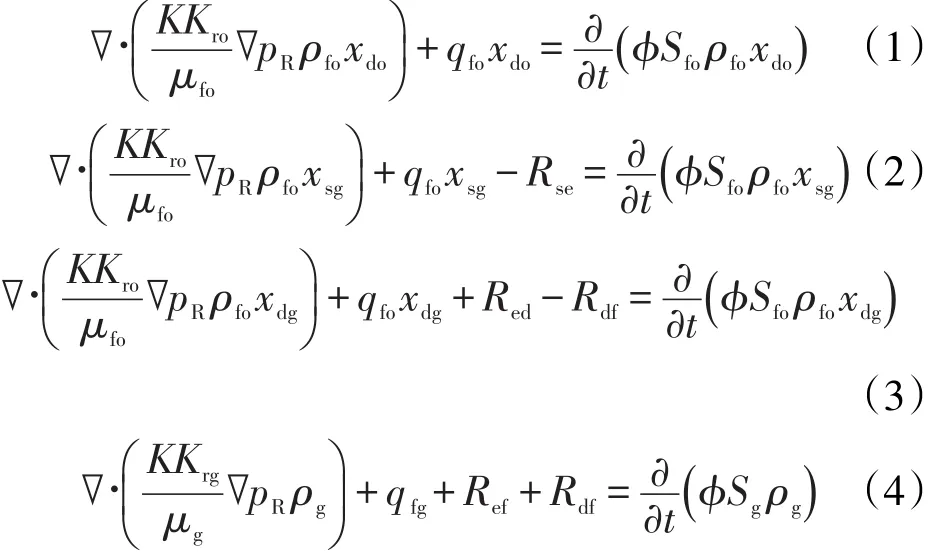
其中

式中：K为绝对渗透率，m2；Kr为相对渗透率；o和g分别为油相和气相；μ为地层流体粘度，Pa·s；fo和fg分别为泡沫油和自由气；pR为地层压力，Pa；ρ为相密度，mol/m3；x为各组分的物质的量分数；do，sg和dg分别为泡沫油相中的纯油组分、溶解气组分和离散气组分；q为源汇项，mol/（m3·s）；t为时间，s；ϕ为孔隙度；S为饱和度；R为相态变化率，mol/（m3·s）；se，ed，df和ef分别为溶解气转化为逸出气、逸出气转化为离散气、离散气转化为自由气及逸出气转化为自由气。

模型初始条件为

式中：pi为原始地层压力，Pa；Sfoi为初始泡沫油饱和度。

模型边界条件为

式中：L为外边界条件；N为边界L的外法线方向；pwf为井底压力，Pa。

2.3 模型相关参数处理

结合泡沫油的油气相对渗透率特点，对常规油气相对渗透率关系进行改进，得到泡沫油的油气相对渗透率关系，同时运用对数混合法则，计算得到不同饱和度下气相对泡沫油粘度的影响。

2.3.1 气液平衡常数

在气泡成核之前，气液平衡常数等于泡点压力下的实验测定值，在大气条件下不存在过饱和现象，所有的离散气都将从油相中脱离，因此标准状况下的气液平衡常数与实验测定值相等［9］。在泡点压力和标准大气压之间，修正的气液平衡常数满足线性递减关系。当油藏压力小于泡点压力时，在过饱和条件下，可通过原油中过饱和溶解气的物质的量求得修正的气液平衡常数，其表达式为

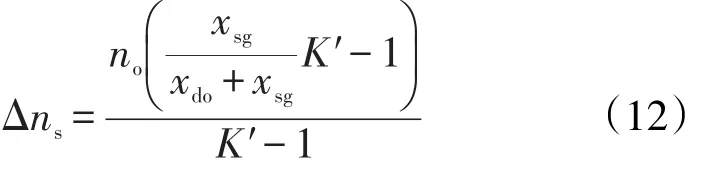
式中：Δns为原油中过饱和溶解气的物质的量，mol；no为油相的物质的量，mol；K′为修正后的气液平衡常数。

2.3.2 相态变化率

气相相态变化率与过饱和溶解气量、时间及气相衰竭系数有关，由此得到溶解气转化为逸出气、逸出气转化为离散气、逸出气转化为自由气的相态变化率分别为

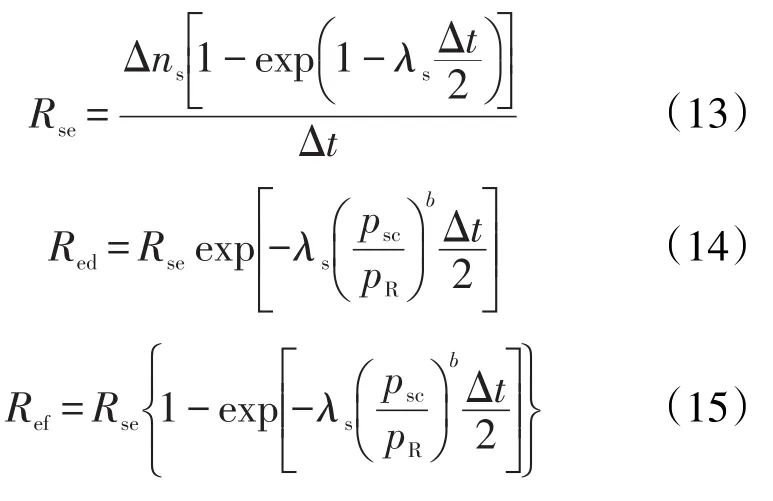
式中：λs为气相衰竭系数，s-1；Δt为时间步长，s；psc为标准大气压，Pa；b为气泡生长指数。

离散气由初始存在的离散气、逸出气新生成的离散气及相邻网格流入的离散气3部分组成。离散气转化为自由气的相态变化率为

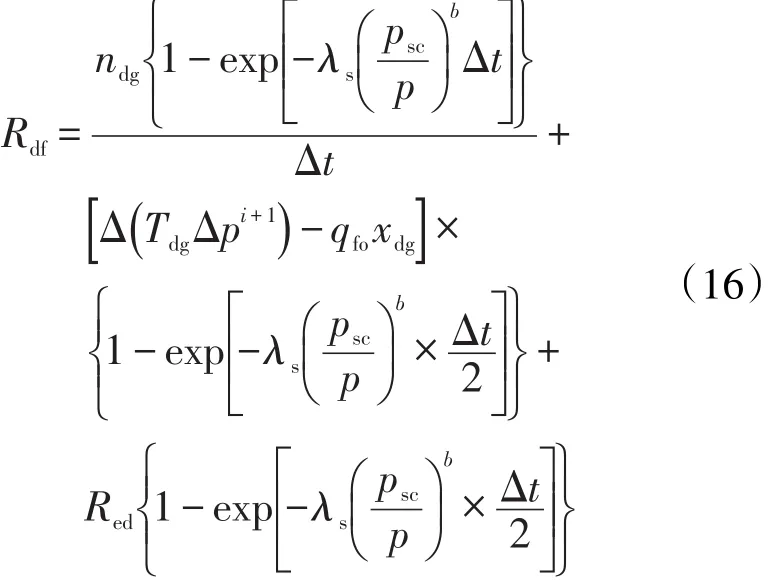
式中：ndg为离散气的物质的量，mol；Tdg为离散气的传导率，mol/s；Δp为压力降，Pa；i为时间步数。

2.3.3 泡沫油粘度

目前仍没有有效测定泡沫油粘度的方法，但泡沫油粘度与地层油粘度相似，在不同饱和度下的粘度不同，因此利用对数混合法则，泡沫油粘度的计算式为

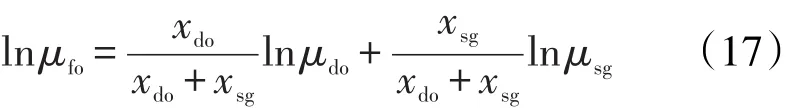
2.3.4 泡沫油的油气相对渗透率关系

泡沫油的流动特征表明其为典型的非牛顿流体，在油藏条件下泡沫油的油气相对渗透率关系尚不清楚。由于离散气与原油一起运移，所以将其视为油相的一部分，结合PVT及压力衰竭实验数据对油气体积进行校正，可计算得到泡沫油的油气相对渗透率关系［10］。

2.4 模型求解

结合泡沫油各组分质量守恒方程，可知模型中只存在4个独立的未知变量，即Sfo，p，xsg和xdg。通过对相关参数的处理，首先得到模型中的Rse，Red，Ref，Rdf和 μfo，然后利用高斯消元和追赶法隐式求解 p，显式求解Sfo，xsg和xdg。

3 模型可靠性验证

所建模型考虑了泡沫油中的气相动态变化过程，涉及热力学平衡和非平衡2个部分的过饱和现象，目前缺少可以进行对比验证的完善模型，而填砂管压力衰竭实验可准确表征稠油冷采的泡沫油现象。为此，笔者利用泡沫油压力衰竭实验对所建泡沫油动态数学模型的可靠性进行验证。

3.1 泡沫油压力衰竭实验

实验室中使用填砂管（或长岩心）压力衰竭实验对稠油自然衰竭开采过程进行模拟，可以得到明显的泡沫油现象，如泡沫油阶段产量迅速增加，且压力持续稳定、具有较高的采油速度以及较低的生产气油比。实验器材与常规溶解气驱压力衰竭实验类似，实验流程如图1所示。

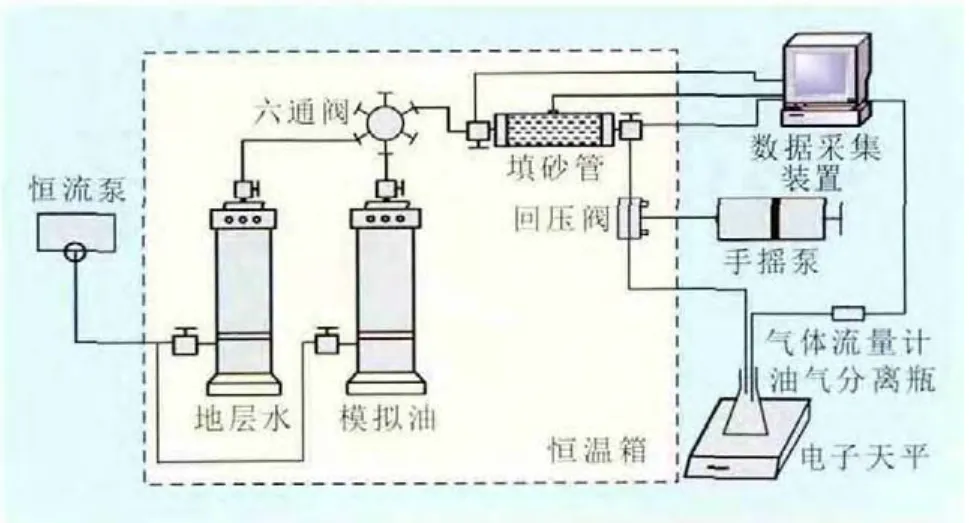
图1 泡沫油压力衰竭实验流程

实验步骤主要分为4步：①通过复配油样得到原始地层条件的模拟油样；②由回压阀控制填砂管内压力在10 MPa左右，饱和2倍孔隙体积的模拟油样；③在填砂管出口端通过回压阀以0.4 MPa/h的速度使压力逐渐下降至大气压；④经油气分离瓶将产生的油气进行分离，并通过电子天平和气体流量计分别对出口端产生的油气进行计量。

3.2 模型验证

针对泡沫油压力衰竭实验，建立了网格数为200的一维正交网格模型，网格规格为3 cm×3 cm×0.25 cm，时间步长为60 s，模型初始温度为55℃，原始地层压力为10 MPa，含油饱和度为96.3%，束缚水饱和度为3.7%，平均渗透率为7 157×10-3μm2，孔隙度为42%，地层原油粘度为5 320 mPa·s，压降速度为0.4 MPa/h。

由图2可以看出：当压力大于4.5 MPa时，累积产油量很小，基本不产气；当压力由4.5 MPa降至2 MPa时，累积产油量迅速上升，累积产气量也逐渐增加；当压力低于2 MPa后，累积产油量增幅变缓，累积产气量急剧上升。这是因为：当压力高于4.5 MPa时，原油中溶解气未分离，由于原油粘度较大，流动性差；当压力为2～4.5 MPa时，溶解气逐渐从油相中分离，在油相中离散成诸多微气泡形成泡沫油，由此形成的油气离散体系使原油粘度降低，流动性增强，由于原油物性明显改善使得产量显著增加；当压力低于2 MPa时，泡沫油中的离散气泡聚并形成自由气，产气量迅速增加。

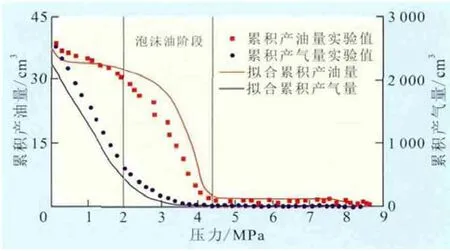
图2 模型拟合结果与实验值对比

对比泡沫油压力衰竭实验数据与所建模型拟合结果（图2）可知，当压降速度为0.4 MPa/h时，实验值与拟合值的平均误差为5.3%，说明所建动态数学模型对稠油冷采中泡沫油现象有较好的模拟效果。

4 产量预测与参数敏感性分析

应用所建模型对不同压降速度下的泡沫油产量进行预测，并分析气相衰竭系数和气泡生长指数对泡沫油产量变化的影响规律。

4.1 不同压降速度下产量预测

在气相衰竭系数为0.002 s-1和气泡生长指数为1.01的条件下，改变数学模型的压降速度进行计算。计算结果（图3）表明，3个压降速度下的累积产油量与压力曲线形状与泡沫油压力衰竭实验结果相似，均存在明显的泡沫油生产阶段，泡沫油生产阶段累积产油量明显上升，并且压降速度越大开采效果越好。

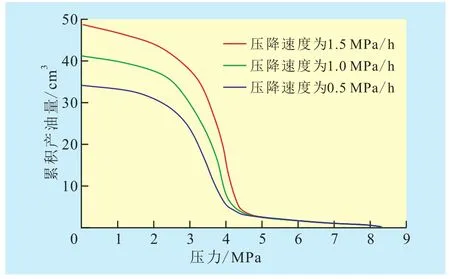
图3 不同压降速度下动态数学模型预测结果

4.2 模型参数敏感性分析

气相衰竭系数 由不同气相衰竭系数下的产量预测结果（图4）可以看出，泡沫油的产量随时间呈先增加后减小的趋势，气相衰竭系数越小，曲线凸起越大，泡沫油的产量越大。这是因为：当地层压力小于泡点压力时出现过饱和现象，气相衰竭系数影响过饱和溶解气转化为离散气的数量，进而决定微气泡的分布状况，对泡沫油生产机理产生较大影响；气相衰竭系数越小，油相中溶解气转化形成的微气泡越多，泡沫油体系越成熟、分布越广泛，更有利于泡沫油流动，泡沫油的产量也越大。

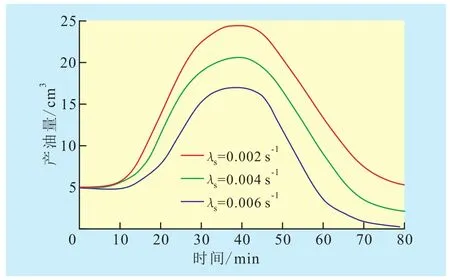
图4 气相衰竭系数与泡沫油产量的关系

气泡生长指数 不同气泡生长指数的产量预测结果（图5）表明：泡沫油的产量与时间的关系曲线同样存在明显凸起，泡沫油的产量随时间呈先增加后减小的趋势；气泡生长指数越大，泡沫油的产量曲线凸起出现的时间越晚，这主要是由于气泡生长指数影响泡沫油阶段形成微气泡的生长速度和周期，气泡生长指数越小，油相中溶解气转化为气泡的时间越短，泡沫油形成得越早，气泡存在的时间越长，泡沫油体系成熟得越早。

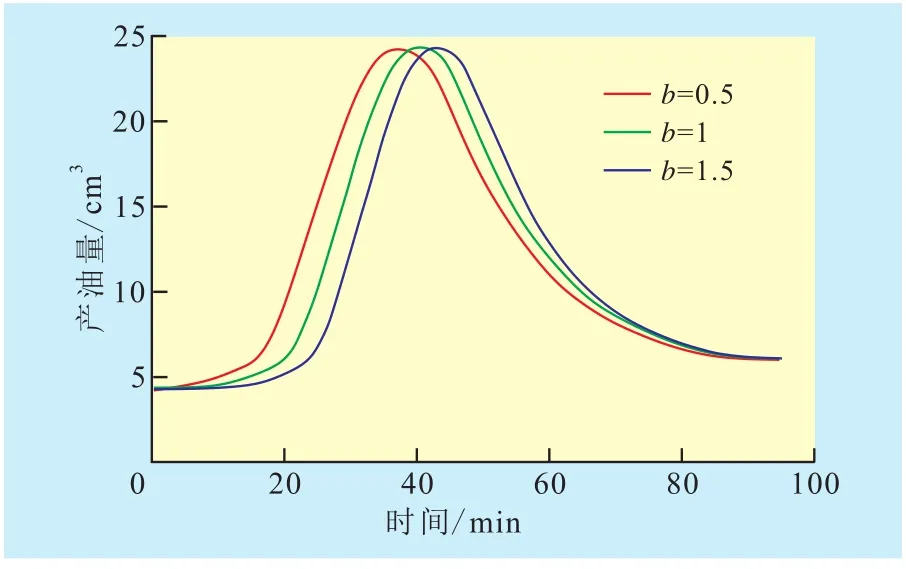
图5 气泡生长指数与泡沫油产量的关系

5 结论

在稠油溶解气驱泡沫油机理研究的基础上，建立了泡沫油动态数学模型，并利用泡沫油压力衰竭实验，验证了所建泡沫油动态数学模型的可靠性。

气相衰竭系数影响泡沫油中形成微气泡的数量，其值越小，泡沫油的产量越大；气泡生长指数影响泡沫油的形成时间，其值越小，泡沫油形成得越早。两者的影响主要集中在生产中后期形成泡沫油的阶段，验证了泡沫油气相变化机理对稠油冷采溶解气驱开发的重要作用。

［1］ Maini B B，Sarma H K，George A E.Significance of foamy-oil be⁃havior in the primary production of heavy oils［J］.Journal of Cana⁃dian Petroleum Technology，1993，32（9）：50-56.

［2］ Huerta M，Andarcia L.Dimensionless characterization of transient pressure volume behavior for foamy oils［C］.SPE 120754，2009.

［3］ 张军涛，吴晓东，李波，等.稠油冷采泡沫油溶解气驱油藏开发动态数值模拟［J］.油气地质与采收率，2012，19（3）：81-83.

［4］ 王勇，吴晓东，韩国庆，等.泡沫油油藏数值模拟研究［J］.油气地质与采收率，2012，19（2）：78-80.

［5］ 张艳玉，孙晓飞，李星民，等.出砂冷采稠油油藏泡沫油研究进展［J］.油气地质与采收率，2013，20（1）：63-66.

［6］ Sheng J J，Hayes R E.A dynamic model to simulate foamy oil flow in porous media［C］.SPE 36750，1996.

［7］ Geilikman M B.Dynamic effects of foamy fluid flow in sand pro⁃duction instability［C］.SPE 30251，1995.

［8］ 岳湘安，王尤富.提高石油采收率基础［M］.北京：石油工业出版社，1990.

［9］ 盛加平，周学龙.油田热采数值模拟参数计算和选择［J］.特种油气藏，1995，2（3）：15-21.

［10］ 秦积舜，陈兴隆.油藏条件下泡沫油的油气渗流规律研究［J］.西安石油大学学报：自然科学版，2007，22（2）：116-118.