基于风洞试验的圆弧形硬帆最佳攻角

薛树业， 胡以怀， 何建海， 曾向明

(上海事事大学 商船学院，上海 201306)

基于风洞试验的圆弧形硬帆最佳攻角

薛树业， 胡以怀， 何建海， 曾向明

(上海事事大学 商船学院，上海 201306)

由于风帆在什么攻角下对船舶产生的推力最大，且对船舶稳性的影响最小是衡量风帆性能的重要因素，因此对最佳风帆攻角进行研究，使控制系统准确地控制风帆，从而使风帆实现最佳的节能减排效果。通过对5种具有优良空气动力性能的圆弧形薄翼硬帆模型进行风洞试验，得到一系列的帆性能参数。通过对这些参数进行分析，得到圆弧形薄翼风帆最佳攻角的规律及风帆最佳操纵曲线，可为风帆的控制提供参考。

船舶工程；风洞试验;圆弧形薄翼硬帆;最佳攻角;风帆操纵

随着能源危机日益凸显以及人们对环境保护日益重视，新能源的开发和利用成为时代发展的潮流。2009年召开的国际海事组织第59次环保会上，新能效设计指数、现有船舶能效营运指数、船舶能效管理以及自愿验证4个通函被作为船舶节能减排的重要标准[1]；2013年6月，欧盟正式推出航运业碳排放监管草案，旨在从2018年起对船舶温室气体的排放进行强制监测，以降低温室气体排放对气候的破坏。由此可见，研究船舶节能减排技术刻不容缓。

目前，风能和太阳能是船舶营运中能够有效利用的清洁能源。相比之下，风能可被航行中的船舶直接转化为船舶的推力，无需经过二次转化，因此更容易被利用。风帆助航船舶有很大的发展空间，能够满足船舶节能减排的要求，其中风帆的研究是风帆助航技术的核心内容之一。风帆在什么攻角下对船舶产生的推力最大且对船舶稳性的影响最小，是衡量风帆性能的重要因素。圆弧形薄翼硬帆与其他帆具相比具有优良的流体动力性能[2-4]，且结构简单、便于控制。以该类型风帆为模型进行风洞试验，研究最佳风帆攻角的问题，得出风帆操纵规律，为风帆的控制提供参考。

1 风帆攻角的研究现状

目前，最佳风帆攻角的研究主要集中于风帆能否为船舶提供最大的推力。文献[2]以船模水池试验代替风洞试验，将帆模倒置于水中，利用水流与帆的相对运动获得风帆的流体动力性能,得到风帆的最佳攻角与最佳转角之间的规律；文献[5-6]在风帆小攻角(lt;35°)的假设下，利用湍流边界层基本定理对圆弧形风帆进行流体动力计算，得到风帆升力和阻力与风帆攻角的函数关系式；文献[7]利用线性插值的方法对不同展弦比、拱度比的圆弧形风帆攻角进行数值计算，得到最佳攻角的数值表达式。

此处利用风帆模型的风洞实验数据，对5种不同展弦比、拱度比的圆弧形薄翼硬帆模型的空气动力性能进行研究。通过对试验数据进行整理和分析，找出有关风帆攻角的规律，得出最佳风帆攻角的相关结论, 最终计算出最佳操帆曲线。

2 风洞试验

2.1试验风洞

试验所用风洞是一座吸入式低速直流边界层风洞，其试验段长度14 m，截面为正方形，宽1.8 m，高1.8 m。试验风速可以在2～30 m/s连续调节，收缩比为3.56，紊流度lt;1%, 流场品质良好。风洞的试验段内配备有试验转盘，可通过计算机控制电机精确地调节转盘的转角，模拟来流与模型间的偏角(即风帆攻角α)。

2.2风帆动力特性

圆弧形风帆模型上受到的气动力由风轴坐标系上分解的各个力和力矩的分量表示。风轴坐标系[8](见图1)为直角坐标系O-LDZ，原点O位于模型底板中心，Z轴竖直向上，在水平面内的L轴为升力方向，D轴为阻力方向。风帆受到的气动力被分解为与来流方向一致的阻力FD、垂直于来流方向的升力FL、对桅杆的扭矩M，力矩的参考点为坐标原点O。

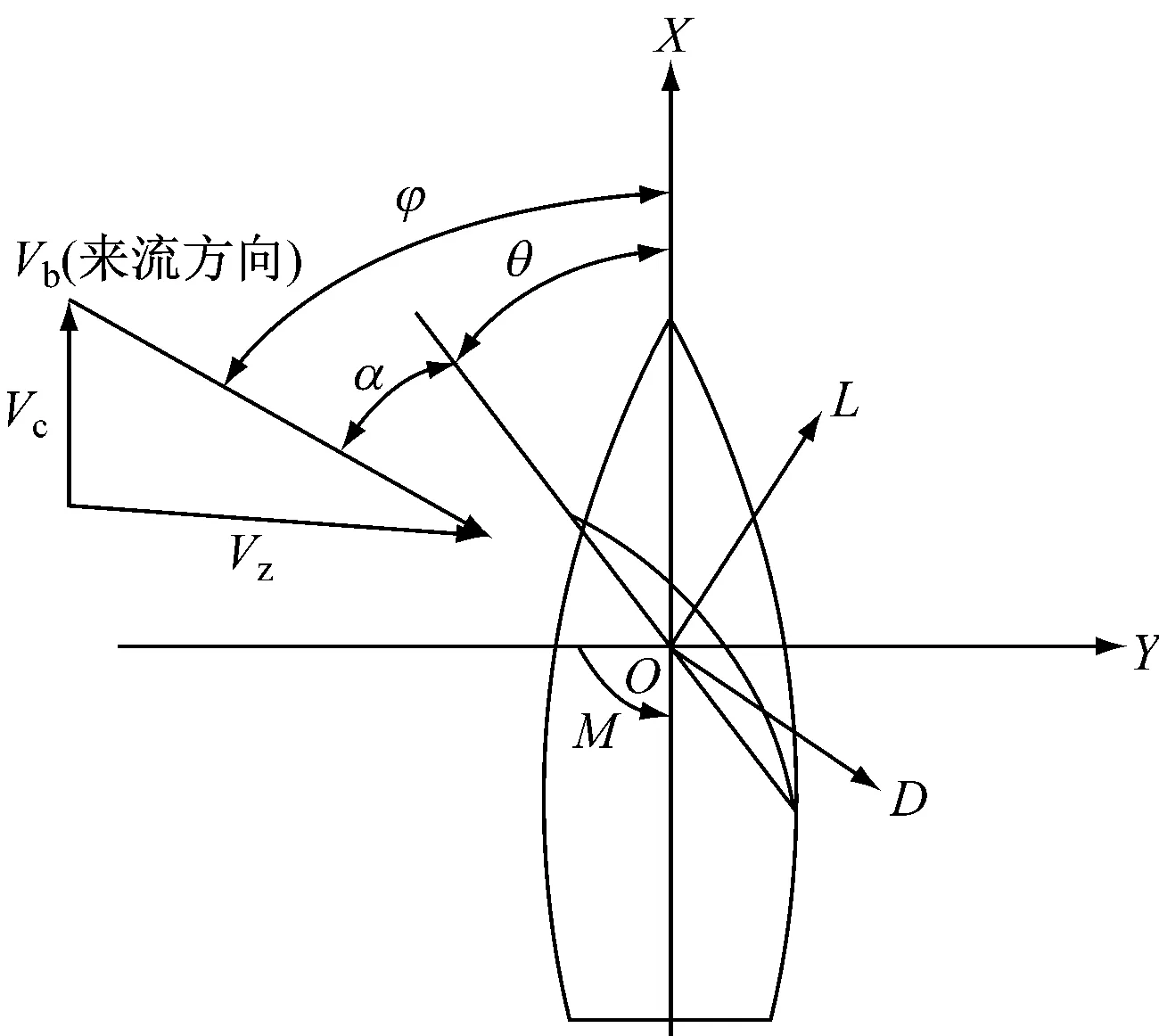
图1 风轴坐标系

风帆对船舶产生的助推力为

T=FLsinφ-FDcosφ

(1)

风帆对船舶产生的横漂力为

H=FLcosφ+FDsinφ

(2)

以无因次数的形式表示为

CT=Clsinφ-Cdcosφ

(3)

CH=Clcosφ+Cdsinφ

(4)

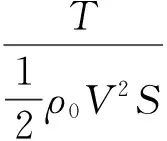
2.3试验内容

风帆模型测力的风洞试验(见图2)是在均匀流场(风速为15 m/s)中进行的，主要内容为A，B，C，D和E 5种圆弧形薄翼风帆模型的测力试验。试验的风帆攻角范围为0°～90°，每隔5°测量一次。对于上述试验中的每一次测量，进行一次不吹风的测量，由两次测量的差值求得气动力。

图2 风洞试验

2.4试验结果

通过5组风洞试验，得到了A，B，C，D和E 5种圆弧形薄翼风帆模型的Cl-Cd曲线(见图3)，以及CM-α曲线(见图4)。由这些曲线可知，对于不同展弦比、拱度比的风帆，其升力系数、阻力系数、扭矩系数随攻角的变化趋势是相同的。

从5组Cl-Cd变化曲线可以看出：在小攻角(0°～30°)范围内，Cl，Cd与α成正相关性，Cl的变化速率比Cd快；在到达某一攻角α(30°附近)时，Cl达到极值，此处即为曲线的拐点；此后Cl急剧下降，Cd激增，Cl与α成负相关性，Cd与α成正相关性。由圆弧形风帆与机翼的空气动力性能相似可知，在Cl-Cd曲线拐点处的这一现象称为失速，这是大攻角时翼后空气气流发生涡流分离的缘故。[10]

从CM-α变化曲线可以看出，在Cl-Cd曲线拐点处，CM也达到了极值，说明在这种情况下，作用在风帆上的力达到了最大。

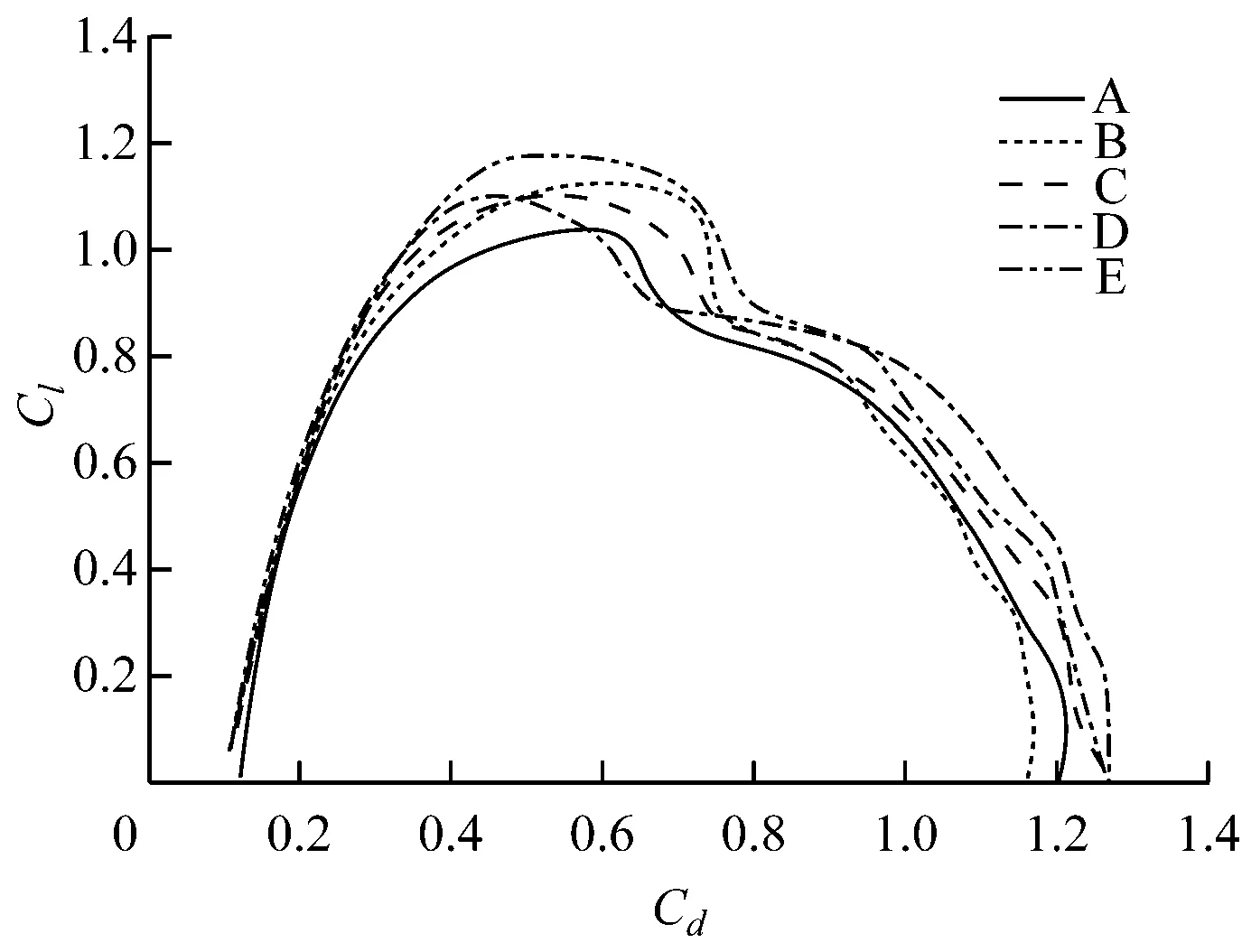
图3 各模型帆的Cl-Cd曲线

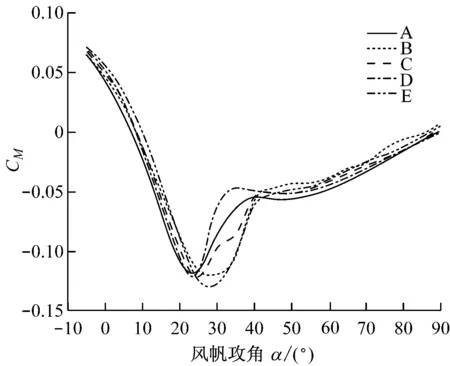
图4 各模型帆的CM-α曲线

3 风帆模型最佳风帆攻角

风帆对船舶产生的助推力可增加航速、降低主机耗油率，因此应使其在一定条件下达到最大值。横漂力会使船舶偏离预定航线、航程增加，为使船舶回归到预定航线上就必须增加船舶耗油量；同时，横漂力的存在会给船舶稳性带来很大影响，如船舶横摇角变大等。因此，横漂力对船舶是有害的，应使助推力达到最大时横漂力处于可控范围内。

在一定的表观风速下，升力系数、阻力系数和扭矩系数是随着风帆攻角α变化的，因此助推力系数和横漂力系数可表示为α与φ的函数，即

CT=f(α,φ)

(5)

CH=g(α,φ)

(6)

由船舶和风帆的对称性，只需研究风向角0°～180°，风帆攻角0°～90°的范围。最佳风帆角α可定义为：当φ，α满足一定关系时，使助推力系数达到最大，同时有横漂力系数最小，此时的风帆攻角是最优的。当然，该定义是最理想的，实际上在助推力系数最大时，横漂力往往不是最小的，这就需要使横漂力系数控制在船舶允许的稳性限度内。

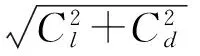
从表1中的试验数据可以看出，当α≥20°时，近似地有α=β，即

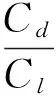
(7)

此时有

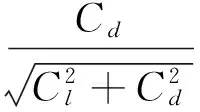
由模型帆E在不同攻角下的系数模量数据可知，小攻角(αlt;20°)下的系数模量要小于大攻角下的系数模量。因此，在推导最佳风帆角的过程中，可以只考虑中等攻角(20°≤αlt;40°)和大攻角(40°≤α≤90°)的情况。下面根据式(7)的近似关系求最佳风帆攻角。

由式(3)得

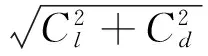
(8)

由式(4)得

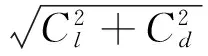
(9)

欲使推力系数最大，必须有sin(φ-α)=1。根据φ与α的取值范围，其应满足φ-α=90°，而此时cos(φ-α)=0，横漂力系数达到最小。这种情况正好满足最佳风帆攻角的要求。在满足φ-α=90°的条件下，需寻找最大的系数模量A。模型帆E的系数模量随攻角α先变大后变小，在30°攻角时有最大值，因此其最佳风帆角应为30°，此时的风向角为120°，最大助推力系数CTmax=1.328 18，同时横漂力系数CH=0。该结论与文献[1-2]中的结论相符。

在120°风向角下，通过式(3)计算得到的最大推力系数为

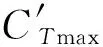
0.638 39cos120°=1.327 85

通过式(4)计算得到的横漂力系数为

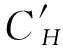
0.638 39sin120°=-0.029 48

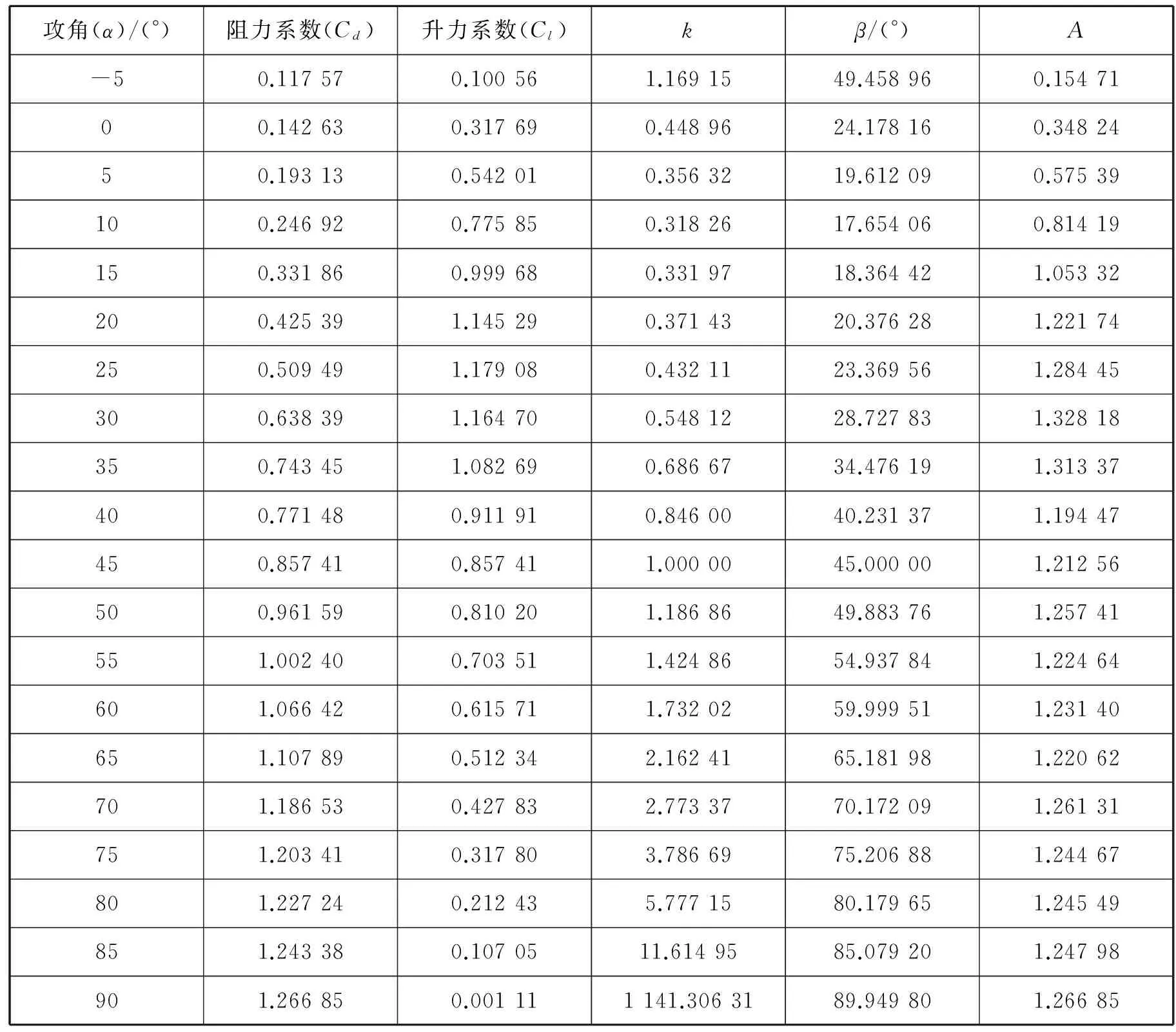
表1 模型帆E的相关风洞试验数据

通过计算模型帆A，B，C，D的风洞试验数据也可得到与模型帆E相同的结论。模型帆A，B，C，D，E的最佳风帆角分别在25°，30°，30°，25°，30°附近，此时扭矩系数CM也达到极值点。这说明，当风帆处于最佳风帆角的位置时，风帆上的载荷最大。不同展弦比、拱度比的风帆，其最佳风帆攻角是不同的。最佳风帆攻角的范围在25°～30°。针对某一具体风帆，其最佳风帆攻角可通过风洞试验确定。

4 风帆操纵曲线

根据式(8)和式(9)计算得到的最佳风帆攻角只是一种特殊情况。对于E模型帆，当风向角为120°、风帆攻角为30°时，其助推效果是所有风帆角中最佳的。但在实际中，风向角是不断变化的，因此需根据式(3)和式(4)求出不同风向角下的最大助推力系数、最大助推力系数下的横漂力系数，确定可操帆区间，得出最佳的风帆攻角，绘制出操帆曲线。图5为最大助推力系数及最大助推力系数下的横漂力系数随风向角的变化曲线图。从图5可以看出：在风向角lt;17°时，风帆对船舶不产生助推力，而此时的横漂力较大；在风向角为68°时，风帆产生的最大助推力与横漂力相等；在68°以后，风帆产生的最大推力大于横漂力，且最大助推力趋于不变，而横漂力不断减小。因此，为使船舶尽可能小地偏离航线，同时使产生的助推力最大，建议在风向角gt;68°时张帆，lt;68°时收帆，以达到最佳的助航效果。图6显示了风帆能提供最大助推力时的攻角曲线，风帆操

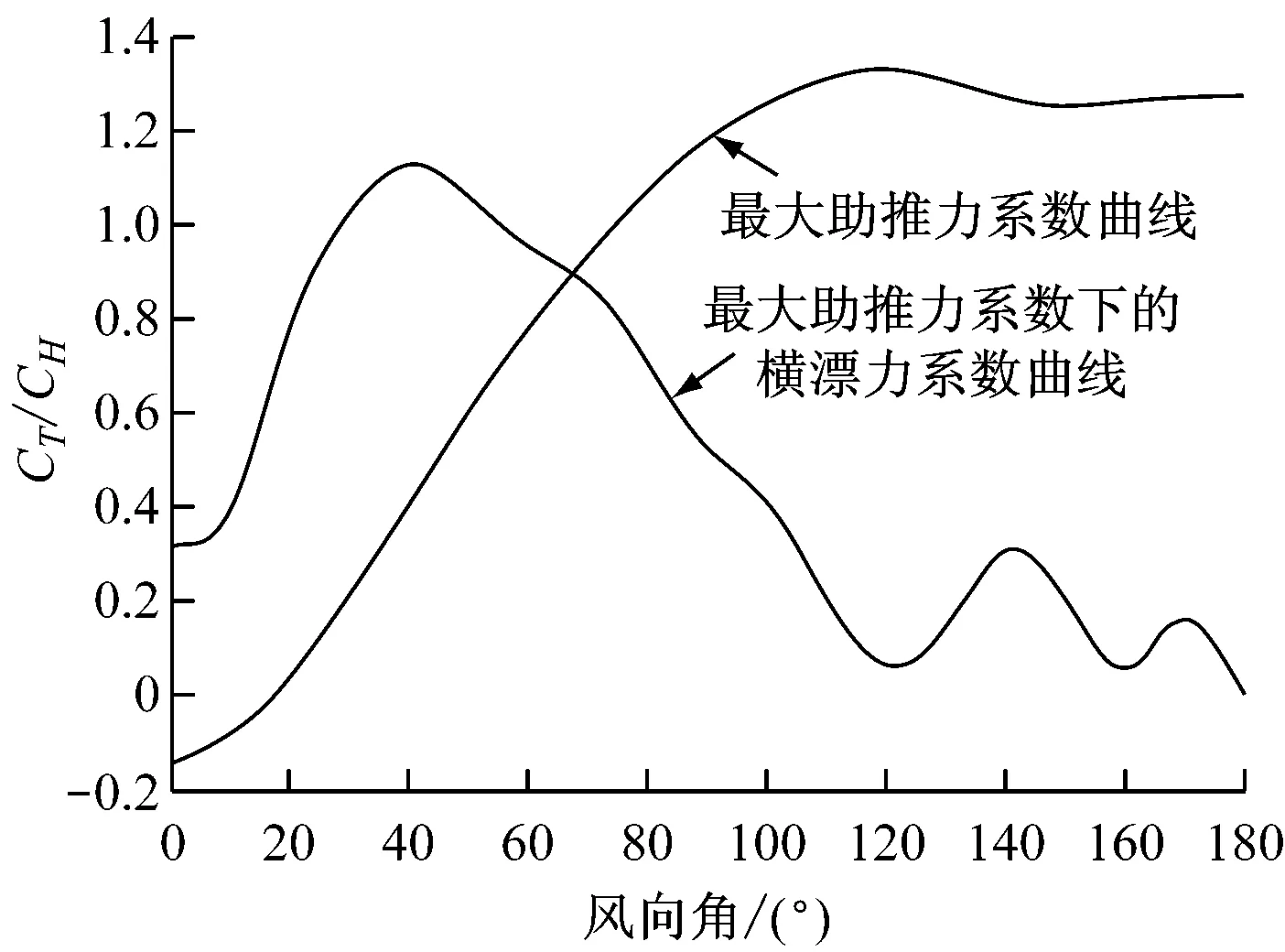
图5 助推力系数和横漂力系数随风向角的变化曲线图

图6 操纵风帆的最佳攻角曲线图

纵机构可按照最佳风帆攻角曲线随不同风向角的变化来调整风帆。

5 结 语

通过对不同展弦比、拱度比的风帆模型进行风洞试验，对数据进行分析，得到了圆弧形薄翼风帆最佳攻角的规律。不同展弦比、拱度比的风帆最佳风帆攻角是不同的，最佳风帆攻角的范围为25°～30°。具体风帆攻角的确定还需通过进一步的风洞试验。由于本风洞试验中的相关数据是在风帆攻角每变化5°测定的，因此在确定每种风帆最佳攻角时，还需进一步缩小攻角的变化幅度，测量相关数据，以求得更准确的结果。根据最佳风帆攻角确定风帆最佳操纵曲线，使控制系统对风帆进行准确的控制，以使风帆发挥最大的节能减排作用。

[1] 曾向明,胡以怀,王友聪.不同形状风帆的风洞试验[J].上海海事大学学报,2010，31(4):28-31.

[2] 张云彩,盛振邦.圆弧型风帆空气动力性能的试验研究[J].中国造船，1983(4):1-10.

[3] 朱健行,李志春.船用风帆选型及流体动力学特性试验[J] .民用船型开发通讯，1990，62(3)：47-49.

[4] 陈威,高泽世,胡以怀,等.辅助船舶航行的圆弧型风帆流体动力性能分析[J]中国航海，2011，34(1):30-35.

[5] 廖铭声.圆弧型风帆设计的流体动力计算[J].舰船科学技术，1997(3):13-18.

[6] 廖铭声.圆弧形风帆的阻力研究与计算[J].船舶工程，1997，27(6)：13-15.

[7] 陈顺怀,冯恩德.风帆助航船帆性能及节能效果的预报方法[J].武汉交通科技大学学报,1996，20(3):342-348.

[8] 王友聪.船舶风帆风洞特性试验研究[D].上海:上海海事大学,2009.

[9] 胡以怀,李松岳,曾向明. 翼型风帆的气动力学分析研究[J].船舶工程，2011，33(4):20-24.

[10] 缪国平.帆船运动的力学原理[J].力学与实践，1994(1):9-18.

BestAngleofAttackofCircular-ArcSailsDeterminedbyWindTunnelTests

XUEShuye,HUYihuai,HEJianhai,ZENGXiangming

(Merchant Marine College, Shanghai Maritime University, Shanghai 201306, China)

The sails on board ship should generate maximum thrust and have minimal impact on stability of the ship under the best attack Angle. The study of the best angle of attack helps the control system to accurately control sails and make sails most effective in energy conservation and emissions reduction. The parameters of five different designs of circular-arc sails, which have excellent aerodynamic performances, are obtained through a series of wind tunnel tests. The best angle of attack and the curves of sail manipulation are determined based on test data. This study may help the design of the sail control.

ship engineering; wind tunnel test; circular-arc sail; best angle of attack; sail manipulation

2014-04-28

上海市科委资助项目(08210511800)；上海海事大学研究生创新基金资助项目(GK2013044)

薛树业(1989—),男，河南济源人，硕士生，研究方向为船舶动力装置及新能源。E-mail: xueshuye111111@126.com

胡以怀(1964—),男，江苏高邮人，教授，博士生导师,研究方向为船舶动力装置及新能源。E-mail:yhhu@shmtu.edu.cn

1000-4653(2014)03-0059-04

U674.926

A