基于曲波变换的接触网磨耗图像增强研究
2014-11-27汪芳莉顾桂梅
汪芳莉,顾桂梅
(兰州交通大学自动化与电气工程学院,甘肃兰州 730070)
在电气化铁道供电系统中,由于多种因素的影响,使得电力接触导线存在非常严重的磨损。电力接触导线为无备用设备,一旦发生故障,将使得列车中断运行,造成重大的经济损失[1]。因此,在铁道电气化系统中,为保持接触网良好的动态性能,必须对接触网几何参数进行定期检测。
采用立体视觉技术的接触网图像检测法,因其具有检测精度高、动态实时检测等优点,成为接触网检测的发展趋势[2,3]。然而,在检测过程中受列车振动、环境、天气等因素的影响,采集到的图像往往存在局部或整体对比度差、边缘模糊等不足,接触网磨耗断面不是很清晰。因此,能否对磨耗断面图像进行有效的增强,提高图像与背景的对比度,同时又有效保持或抑制非磨耗信息,是后续处理和分析的关键步骤,也是接触导线磨耗分割和识别的基础。
图像增强方法主要分为空域法和频域法两类。传统的增强方法属于前者如灰度变换、直方图均衡化、空域平滑和锐化处理等[4,5]。在频域增强方法中因在时域和频域都有良好的局部特性,使得小波变换广泛应用于各图像增强领域。小波变换对信号的点奇异性表现较好,但对于含有线奇异或者面奇异的高维特征表达能力有限,进而影响了增强效果。为了克服小波变换的局限性,充分利用图像的几何特征,人们提出了基于多尺度理论分析的曲波变换[6,7]。Curvelet变换是在小波变换的基础上引入了方向参量,使得它具有更好的方向辨识能力,对图像边缘具有更优的表达能力,可以更好地区分图像的边缘和噪声。因此很适合增强接触网磨耗图像这类方向性很强的图像。
本文提出一种基于曲波变换的接触网磨耗图像增强算法。该算法以曲波变换为基础,对曲波变换后的图像,在低频领域利用分数阶微分的相关特性进行处理,在高频领域利用曲波系数尺度内和尺度间的相关特性对信号和噪声进行区分,并采用非线性函数对图像细节进行增强。该算法在增强细节的同时,对噪声进行了有效抑制,可获得良好的增强效果。
1 基于曲波域的接触线磨损图像算法
曲波因其对边缘、模糊线等曲线特征具有更高的感知效果,近年来在图像去噪、图像增强等领域得到了广泛应用。1999年Candes等首次提出了Curvelet变换并构造了其框架,对于具有光滑奇异性曲线的目标函数,Curvelet变换提供了稳定和近乎最优的表示[8]。为了简化其实现步骤,提高算法效率,2002年Candes等人又提出来实现简单、更便于理解的第二代Curvelet,即快速 Curvelet变换。
1.1 快速离散曲波变换
在二维空间R2中,定义空间位置参量x、频率域参量ω、频域极坐标γ和θ。假设存在平滑、非负、实值的“半径窗”W(γ)和“角窗”V(t),且满足容许条件[9]

对所有尺度存在j≥j0,定义傅里叶频域的频率窗为

令母曲波为 φj(x),则在尺度 2-j上的所有Curvelet都可由φj旋转和平移得到。引入等距的旋转角序列 θl=2π×2-[j2]×l(l=0,1,…,0≤θl≤2π)和位移参数序列 k=(k1,k2)∈Z2,则连续 Curvelet为

为了便于图像处理的实际应用,定义笛卡尔坐标系下的局部窗为j(ω)=j(ω)Vj(ω),其中
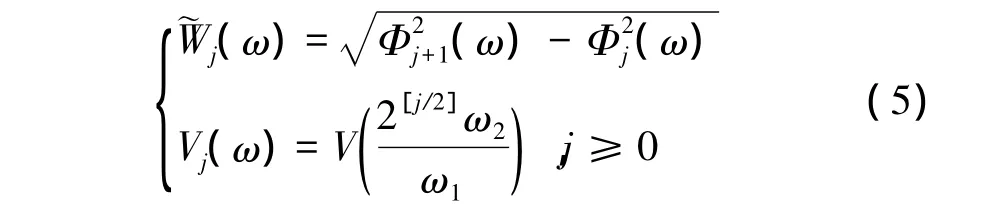
Φ被定义为一维低通窗口的内积

引入等间隔斜率序列 tanθl=l×2[-j/2],tanθl=l×2[-j/2],l=-2[-j/2],…,2[-j2]-1,则

剪切矩阵:Sθ=,则离散 Curvelet定义为

其中,b 取离散值(k1×2-j,k2×2-j/2)。这样离散Curvelet变换定义为

由对图像进行Curvelet变换得到Curvelet系数,分析可知与小波理论一样,曲波的成分也分为粗尺度和细尺度。粗尺度下的曲波不具有方向性,而细尺度下的尺度则具有方向性。而图像的细节信息主要集中在高频领域,即细尺度,在粗尺度中主要表征是图像的概貌。因此,为了提高图像的整体对比度,对曲波域中的高频方向系数和低频系数采用不同方法进行处理。
1.2 低频子带分数阶微分增强
分数阶微分是非整数阶微分,其微分阶次必须是实数或者复数,是整数阶微分的一种推广[10-12]。根据Grumwald-Letnikov定义,分数阶微分是将微积分的阶数由整数扩展到分数推衍而来,即

为分析分数阶微分的滤波特性,先推导其频域定义式。对于任意平方可积的信号f(t)∈L2(R)而言,其阶分数阶微分Fourier变换为


依据式(12)绘出分数阶微分的幅频特性曲线,如图1所示。

图1 分数阶微分幅频特性曲线
从图1可看出,分数阶微分算子对信号有明显的加强作用。对于υ阶微分(0<υ<1),设Ω≫1,当ω>Ω时,信号的高频成分被增强,但其增强的幅度远没有一阶微分增强的大;当1<ω<Ω时,信号的中频成分也被增强,其增强幅度稍比一阶微分小;在0<ω<1信号的甚低频部分,υ阶微分对信号的幅值有一定的提升,且提升幅度稍大于一阶微分。上述性质表明,分数阶微分算子在加强信号中高频成分的同时,对信号的低频成分进行了非线性保留。对于接触线的磨损图像,进行曲波变换后,得到的低频图像包括了磨损图像及背景的主要轮廓信息,高频方向子带包括了边缘细节及噪声,因此对低频子带采用分数阶微分时,既极大地保留了低频平滑信息,又加强了高频细节信息。
数字图像增强处理中,通常对每个像素点及其周围邻域像素点利用分数阶微分掩模算子作微分运算,从而增强图像纹理细节信息。对于图像信号f(x,y),首先依据Grünwald_Letnikov定义式推导一维信号 f(t)的分数阶微分表达式。
设一维信号f(t)在持续区间[a,t]按单位h=1进行等分,可以得到n==[t-a],从而可得到一维信号分数阶微分的差分表达式

由二维傅里叶变换作用的可分离性,图像信号f(x,y)的分数阶微分可分离为在x和y方向上分别进行一维偏分数阶微分运算。采用分数阶差分定义的前3项作为逼近值,以5*5模板为例,定义f(x,y)的偏分数阶微分为
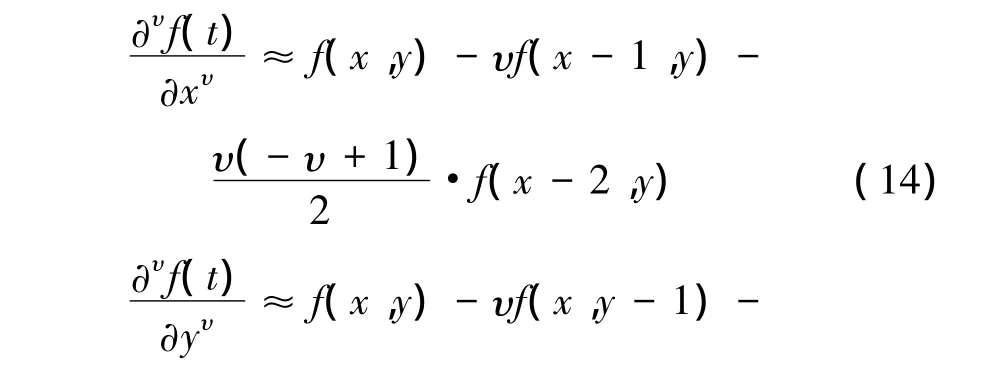

1.3 高频子带系数增强
1.3.1 尺度相关信噪分离
在对图像高频子带进行处理时,图像高频子带在包含很细弱边缘信息的同时还混有不同程度的噪声。因此,在对高频子带进行增强处理时,应对高频系数进行调整,区分出边缘信息及噪声信息。目前,在多尺度去噪中,基于小波变换的阈值算法是主流算法。然而阈值一般根据当前层的小波系数来选取,而未考虑层间小波系数间的关系。实验表明,信号和噪声对应的小波系数在相邻层间的相关性存在着很大差别,曲波变换作为多尺度发展的一个方向,其各层分解后的系数也同样存在着相同联系。具体表现为,在高频尺度,信号所对应的系数在相邻尺度间存在很强的相关性,而噪声所对应系数的相关性则很弱或者不相关。利用曲波相邻层系数相关性的特性,则可以更好的区分出边缘信号和噪声。
设尺度为 j、方向为 l的变换系数 Cj,l(x,y),与其对应的父层系数为 Cj-1,l(x,y),选择去噪函数

上式中去噪函数同时与当前层以及父层曲波系数模有关,只有相邻两层的曲波系数模较小时才将该系数视为噪声分量加以抑制,与只基于当前层曲波系数的去噪方法相比,该方法显然更加合理。
1.3.2 阈值的估计
阈值采用chang等人以广义高斯白噪声为模型,提出基于Bayes准则的自适应阈值,该阈值如下所示

其中,σn为噪声方差;σs为信号标准差。对高频子带系数 Cj,l,k的噪声方差 σn,利用中指估计法得到n=median(Cj,l,k)/0.674 5。信号方差则采用最大似然估计,M和N分别为高频子带的长度和宽度=max(
1.3.3 非线性增益函数
简单增强函数在增强方向子带边缘细节时,也放大了噪声。为克服该缺点,构造一个非线性增强函数十分必要。非线性增强函数必须满足单调性、反对称性。且能抑制较小的系数,保持较大的系数,放大绝对值介于中间的系数。故本文采用如下增益函数


图2 非线性增益函数曲线
该函数在自变量的绝对值接近于0的时候斜率较小,而在自变量的绝对值处于中等时斜率较大,对应于图像的高频子带的增强效果也达到最大,在自变量达到最大时,斜率变为0。
综上所述,基于曲波域的图像增强过程算法步骤如下:
(1)将接触线磨损图像进行Curvelet分解,得到不同尺度的系数;
(2)根据式(14)、(15)对低频子带进行增强;
(3)根据曲波系数在不同尺度间的相关性,将高频子带系数区分出边缘及噪声;
(4)对高频子带的边缘利用式(18)进行增强;
(5)对上述处理后的系数进行逆Curvelet变换得到增强后的磨损图像。
2 实验结果与讨论
为验证算法的有效性,选取一组接触线磨耗图片为测试图片,采用matlab仿真软件作为图像增强软件平台。实验所采用的图片来自于CCD相机对接触线的垂直仰视拍摄,对接触导线分别做 0,1,2,3.5,4.5,6.9 mm的磨损处理。为模拟实际效果,对拍摄到的原始图片加入均方差为30的高斯白噪声进行加噪处理,并分别对加噪后的图像进行传统小波增强,小波变换和低频域分数阶结合增强、快速曲波增强及本文算法增强,对增强后的效果进行对比。实验处理结果及对比如图3所示。
从图3可以看出,小波增强在增强图像边缘的同时,对图像的噪声也进行了放大处理,使得增强后的图像对比度不高;小波和分数阶结合的算法,对噪声的增强有一定抑制作用,但是图像边缘模糊增强不明显;曲波变换对图像的增强明显优于以上两种算法,但是由于曲波变换“楔形基”的线性特点,使得一个系数改变会引起一条直线上的所有值改变,造成图像“划痕”效应明显;相较之下,本文方法在增强图像边缘和提高对比度方面均优于其他算法。

图3 对含噪声接触网磨耗图像进行增强
应用上面实验结果对图像的边缘增强效果,采用客观评价方法对比度改善指数CII来进行衡量,结果如表1所示。从表1的数据也可看出本文算法在对比度提高方面做了明显改善。

表1 对比度改善指数
为了更准确地分析该算法的性能,采用峰值信噪比对各种算法增强后的图像来进行定量分析。实验中分别对原图像加入均方差为10、20、30、40的高斯白噪声,各算法信噪比结果如表2所示。

表2 信噪比比较
由表2数据可以得到,对于不同强度的高斯白噪声,通过小波增强方法和曲波增强方法的对比,曲波增强方法对于接触线这类方向性强的信息具有明显的增强效果;采用与分数阶相结合的方法可以有效地抑制噪声对图像的影响;本文算法对图像信噪比有明显的提高,且随着噪声强度的增加,信噪比变化幅度不大,具有良好的适应性,都可获得较高的信噪比。
3 结论
为了改善接触网磨耗图像边缘对比度,利用曲波变换对线奇异的良好表示特性,结合分数阶微分算子,采用曲波变换对接触网磨耗图像进行增强。本文算法根据曲波域的不同特性,在低频域利用分数阶微分算子进行增强,同时在高频域,结合曲波系数尺度内和尺度间的联系,对图像高频域进行噪声、信号分类,并对分类后的结果进行非线性增强。实验结果表明,本文提出的方法主观上增强了细节和对比度,客观上提高了信噪比和对比度指数。需要说明的是本文算法在得到良好的增强效果的同时,该算法的运行时间相对较长,这是未来需要改进的工作。
[1]于万聚.高速电气化铁路接触网[M].成都:西南交通大学出版社,2002.
[2]韩志伟,刘志刚.非接触式弓网图像检测技术研究综述[J].铁道学报,2013,35(6):40-47.
[3]王华夏,漆泰岳,王摇睿.高速铁路隧道衬砌裂缝自动化检测硬件系统研究[J].铁道标准设计,2013(10):97-102.
[4]程远航,薛定宇.小波和曲波结合的图像增强算法[J].工程图学学报,2009,30(3):100-104.
[5]张桐林,郝宽胜,段汝娇.基于计算机视觉技术的接触网定位器坡度动态测量算法[J].铁道标准设计,2013(1):105-108.
[6]王宪,陶重犇.基于曲波域的指纹增强算法[J].光电工程,2010,37(8):98-103.
[7]李晖晖,刘航.基于第二代Curvelet变换的图像融合研究[J].光学学报,2006,26(5):657-662.
[8]CANDESE J,DONOHO D L.Curvelet-a surprisingly effective nonadaptive representation for objects with edges.TN:Vanderbilt University Press,2000:105-120.
[9]CANDESE J,DEMANET L,DONOHO D L.Fast discrete curvelet transform[R].Applied and Computational Mathematics,California Institute of Technology,2005:1-43.
[10]黄果,蒲亦非.非整数步长的分数阶微分滤波器在图像增强中的应用[J].四川大学学报:工程科学版,2011,43(1):129-136.
[11]杨柱中,周激流,等.基于分数阶微分的图像增强[J].计算机辅助设计与图形学学报,2008,20(3):343-348.
[12]何春,叶永强,姜斌,等.一种基于分数阶次微积分模板的新型边缘检测方法[J].自动化学报,2012,38(5):776-787.
