基于SPN的近距平行跑道容量建模与分析

王洁宁 ，徐宁霞 ，姜高扬

（中国民航大学a.空中交通管理研究基地；b.天津市空管运行规划与安全技术重点实验室，天津 300300）

跑道理论容量对机场规划以及发展具有重要的意义[1-3]。近年，近距平行跑道的容量评估逐渐成为研究热点，其中文献[4]描述了近距跑道在一起一降模式下的数学模型，文献[5]使用时间空间模型建立了近距跑道的理论容量模型，但这些研究都是针对具体的情况建立特定的模型，所建模型的可复用性不强，且缺乏对随机因素的考虑。本文通过随机Petri网建立近距跑道的容量模型，将跑道容量的影响因素转化为相应变迁的激发率，通过调整变迁激发率得到不同情况下的跑道容量及变化规律。据经验和资料分析[6-7]，当起降航班比为1：1、进离场航空器按照降、起交替运行时，能最大可能地避免尾流影响，近距跑道容量可达到最大值，因此本文主要对交替起降模式下的近距平行跑道容量进行计算和分析。

1 随机Petri网模型分析

交替运行近距跑道模型可以抽象成一个六元组SPN=（P，T；F，W，M0，λ），其中（P，T；F，W，M0）是一个P/T 系统，P={p1，…，pn}是库所的有限集合；T={t1，…，tn}是变迁的有限集合；F表示的是弧；W表示的是弧权函数；M0表示的是初始标识[8]。λ ={λ1，λ2，…，λm}是变迁平均实施速率集合。

经证明，飞机到达或起飞时间间隔服从指数分布[9]，因此设Petri网中每个变迁的分布函数为

其中：参数λt是变迁t的平均实施速率，变量x≥0。λt倒数的物理含义为实际运行时起降飞机的时间间隔或在特定条件下所要求的前后机时间。

2 交替起降近距跑道SPN建模

由以上分析，跑道的SPN模型可按以下步骤建模：根据航空器进离港流程分析影响跑道容量的因素，进而建立SPN模型。通过同构马尔科夫链，建立稳态概率表达式，通过调整关键参数λ，对系统进行性能分析。由于跑道影响因素众多，考虑到SPN模型状态空间的庞大性，本文仅考虑影响容量的几个关键因素，主要有尾流间隔、起降比及机型比等。交替起降的近距跑道容量SPN模型如图1所示。

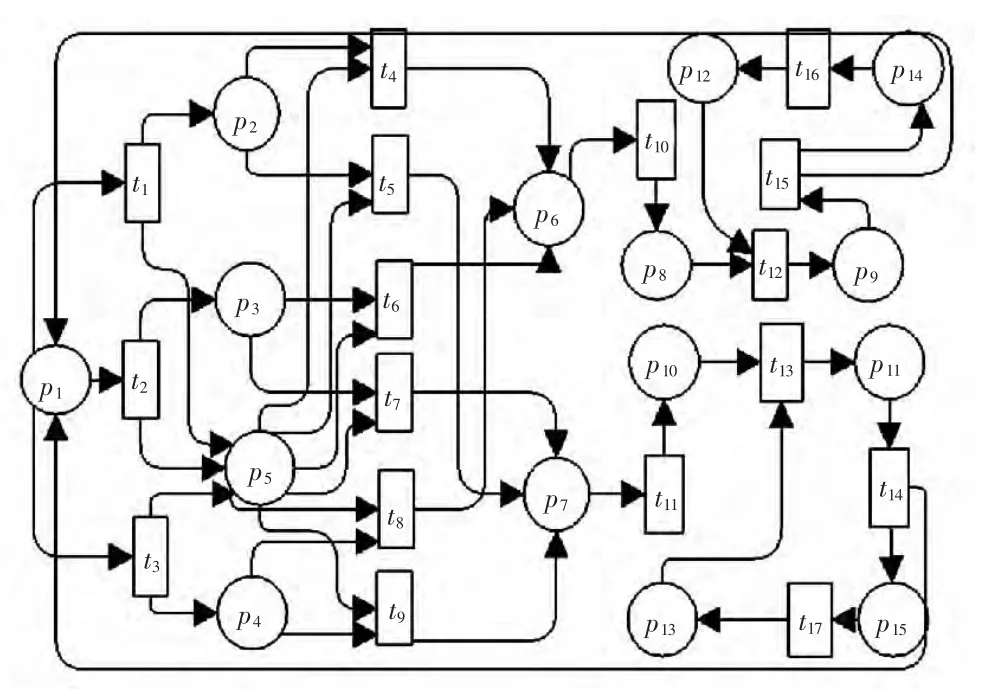
图1 近距平行跑道SPN模型Fig.1 Closely spaced parallel runways SPN model

其中 p1∈{p1，p2，…，p15}为库所的集合，变迁集合为 t1∈{t1，t2，…，t17}。具体含义如表 1 及表 2 所示。

3 构造SPN模型所同构的MC链

图1的近距平行跑道SPN模型初始标识为M0=（1，0，0，0，0，0，0，0，0，0，0，1，1，0，0），随着系统的运行，可得到M1、M2等，进而得到模型的可达树如图2所示。

表1 容量SPN模型库所意义Tab.1 Place significance of SPN capacity model

表2 容量SPN模型变迁意义Tab.2 Transition significance of SPN capacity model

其中，p1、p12与p13中的托肯代表1架飞机、1条可使用的着陆跑道以及1条可使用的起飞跑道。同时经验证，图1的SPN模型符合可达性、有界性、安全性、守衡性、可逆性和活性等要求，即这个模型是正确、安全、有效的。定义λi是变迁ti∈T的平均实施速率，则与图1的SPN模型同构的马尔科夫链如图3（a）和图3（b）所示。

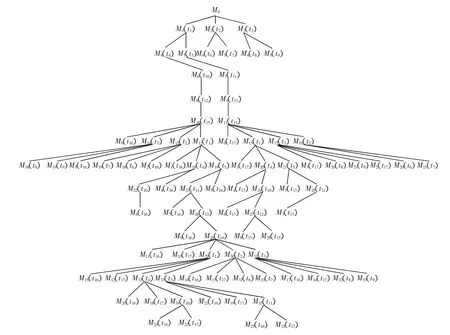
图2 近距跑道SPN模型的可达树Fig.2 Reachability tree of closely spaced parallel runways SPN model

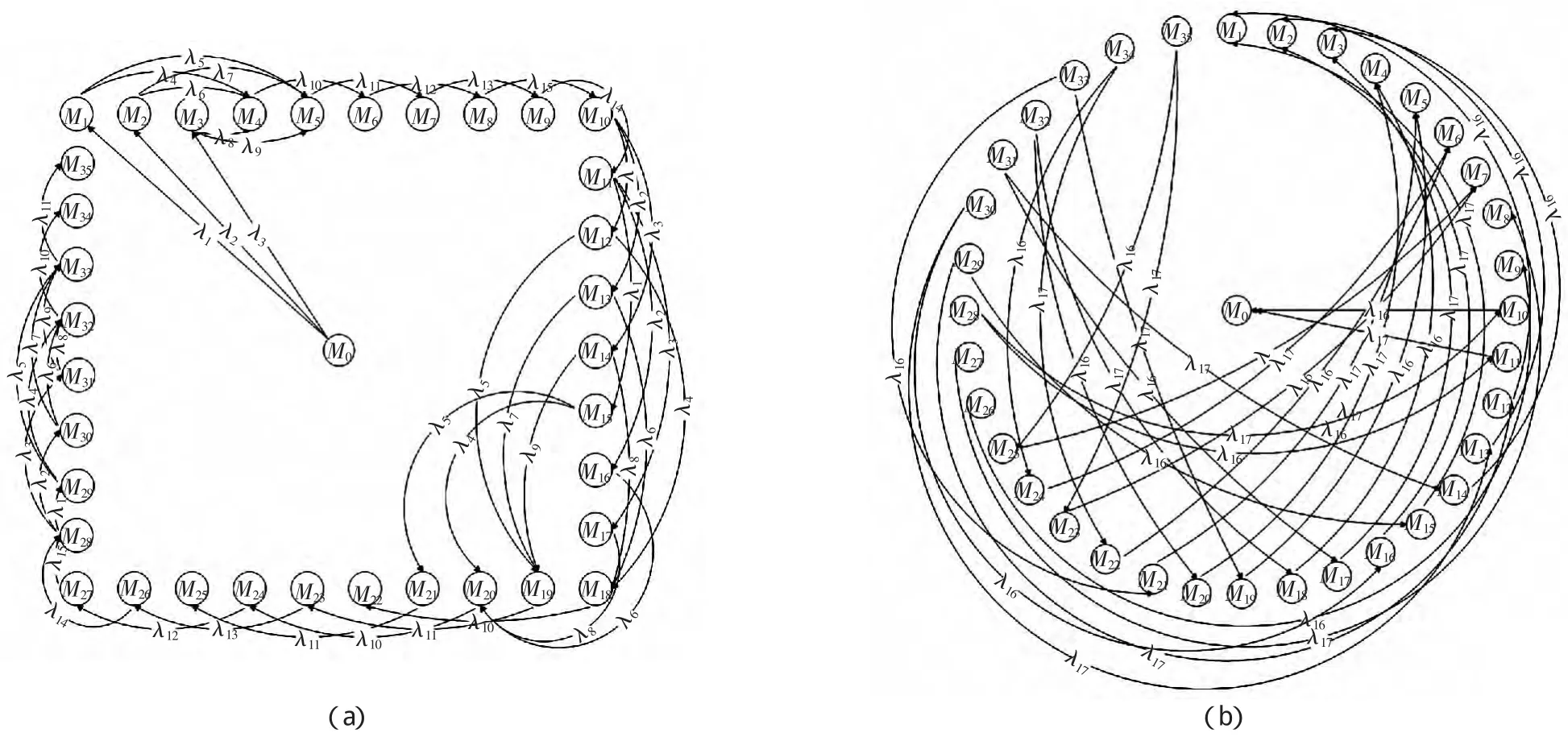
图3 跑道SPN模型的马尔科夫链Fig.3 Markov chain of SPN model

在近距平行跑道的SPN模型中，跑道的容量可由库所p12以及p13的位置标记数来进行统计分析。跑道库所中的托肯没被占用，代表跑道处于空闲；反之，则代表跑道正在使用中。可证明，在给定充分时间的情况下，系统总是可以返回该状态，由近距跑道的SPN容量模型的初始标识，可以获得状态的转移矩阵，由于模型的稳定状态转移概率矩阵庞大，主要用到p12以及p13的稳定状态转移概率，如下所示，其中矩阵Mi={M0，M1，…，M36}表示库所的状态矩阵，未列举项数值为0。

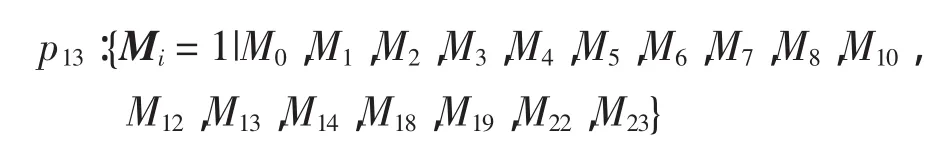
4 基于MC稳态概率的系统性能分析

根据交替起降SPN模型所同构的MC链，进一步得到该模型的稳定状态概率表达式为

1）标记概率密度函数

标记概率密度函数表示在某一特定情况下，任意库所中具有的标识数的概率。对于∀s∈S，∀i∈N，令库所s含有i个标记的概率用P[M（s）=i]表示，就可以从标记的稳定状态概率得到库所s中的标记概率密度函数

其中Mj∈[M0＞且Mj（s）=i]。

2）库所中平均标记数

对于∀si∈S，表示在某一特定情况下，库所si含有的平均标记数，则有

在近距平行跑道SPN模型中，库所p12表示主降落跑道的使用情况，库所p13表示主起飞跑道的利用情况，可利用库所中所包含的平均标记数评估近距跑道容量模型中各个跑道的利用率，进而计算跑道的容量。

跑道容量可由库所p12（主降落跑道）及p13（主起飞跑道）的标记数来进行统计分析。当跑道库所中的托肯没被占用，代表此时跑道处于空闲；反之，当跑道中的托肯被占用了，即库所中的托肯数为0，则代表跑道正在使用中。

根据模型的可达树及库所p12的状态转移概率，主降落跑道中的标记密度函数可以表示为

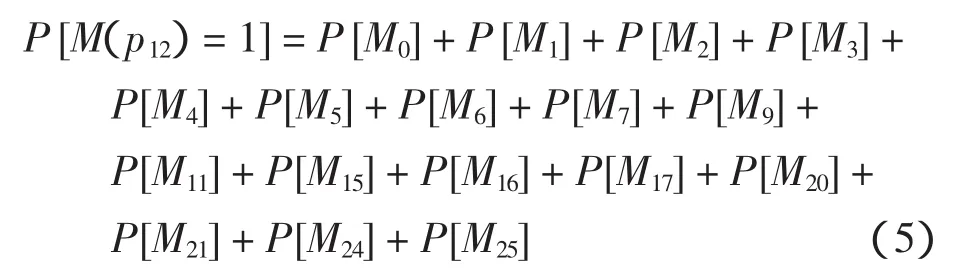
根据模型的状态树及库所p13的状态转移概率，主起飞跑道中的标记密度函数可表示为

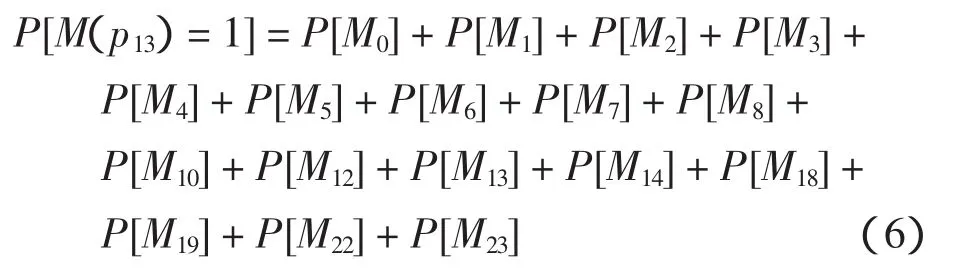
主降落跑道的跑道利用率可表示为

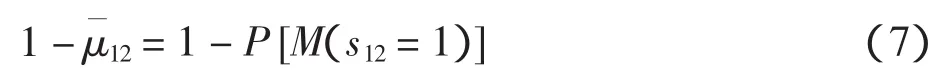
主起飞跑道的跑道利用率可表示为

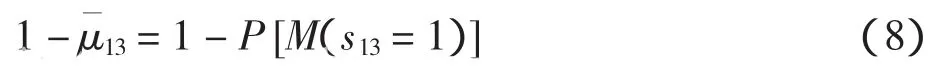
5 算例分析

5.1 跑道理论容量计算

基于某机场进近着陆非雷达尾流间隔标准及相关规定[10]，在计算前后着陆飞机组合相继通过跑道入口时间间隔时，主要考虑前机跑道占用时间、尾流间隔及发布落地许可条件等，选取间隔最大者进行分析。在不受尾流影响的情况下（表3空格对应机型组合），前机和后机通过跑道入口的时间间隔等于“前机跑道平均占用时间+后机飞行4.5 km时间”与前机跑道占用时间的最大者。表3中空格对应的机型组合表示可不考虑尾流影响，按规定的雷达最低间隔标准来考虑。

表3 进近着陆非雷达尾流间隔标准Tab.3 Non-radar wake turbulence separation standards of approach and landing（min）

空格部分的间隔可根据相关数据计算出来。取某机场实际数据，两个降落航班间允许1架航班起飞时，相继降落航班间的平均距离间隔至少为9 km。由降落航班从切入下滑道到接地的平均飞行速度可计算出相应时间间隔，如表4所示。

表4 不考虑尾流的最低雷达间隔Tab.4 Minimum radar separation without consideration of wake

基于以上理论，重型机、中型机以及轻型机两两组合得到前后机型不相同时的相应间隔如表5所示。

表5 前后机型的相应间隔Tab.5 Interval of aircrafts（min）

航空器起降交替运行时，即在两个着陆航班之间插入放行1架航班，在平均意义上起降平均纵向间隔为连续降落航班纵向间隔的一半。基于以上假设，可算出 λ4=λ5=0.018 5；λ6=λ7=0.016 7；λ8=λ9=0.012 3。跑道占用时间也取该机场的实际数据如表6所示。

表6 不同机型起降跑道占用时间Tab.6 Runway occupancy time of landing and takeoff aircrafts

着陆占用跑道时间取均值52 s，起飞占用跑道时间取均值 46 s，即 λ16=0.019 2，λ17=0.021 7。重型机、中型机和轻型机的比例取1：1：1，起飞降落比例为1：1，其它参数为1。基于以上假设可得到λ的取值为{1，1，1，0.018 5，0.018 5，0.016 7，0.016 7，0.012 3，0.012 3，1，1，1，1，1，1，0.019 2，0.021 7}。参数为 1 的变迁就代表在1 s内只运行一次，由于整个近距跑道容量SPN模型运行一次时间相对1 s很大，所以运行时间为1 s的所有变迁，可以默认对整个跑道容量SPN系统产生影响很少，忽略不计。

将λ代入式（2）并计算，可以得到取值为λ时的每个状态标识的稳定状态概率，继而可求出在此时条件下的跑道利用率。此时，将求出的稳定状态概率代入式（5）中，计算出库所p12代表的主降落跑道中的标记密度函数为

则主降落跑道的跑道利用率为

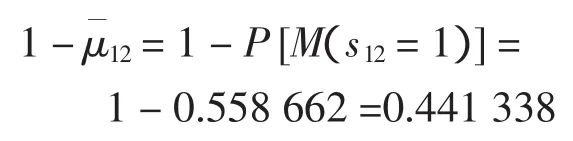
跑道占用时间平均值为52 s，所以一起一降模式下，主降落跑道的跑道容量为

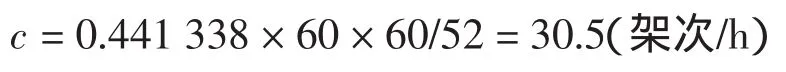
同理，库所p13代表的主起飞跑道中的标记密度函数可表示为

则主起飞跑道的跑道利用率可表示为

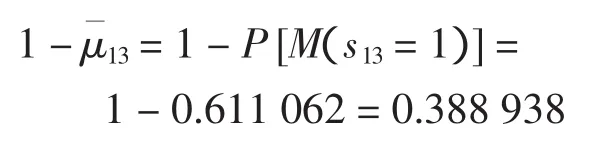
跑道占用时间平均值为46 s，所以一起一降模式下，主降落跑道的跑道容量为

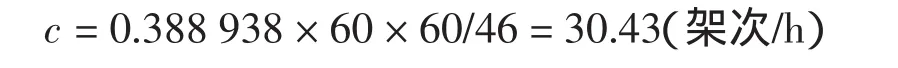
此时，跑道容量为61架次/h，经对比，该数据与某机场的实际运行数据相符。

5.2 中型机对跑道容量的影响

随着民航业的快速发展，大中型航空器所占市场比例越来越大，同时，轻型机的比例也越来越少，目前，国内正在运营的机型是以中型机为主。所以以雷达尾流间隔标准、跑道占用时间以及发布落地许可等条件为基础，以中型机所占总机型比例为变量，分析在中型机比例不断增大的情况下，对近距跑道容量的影响趋势。

当中型机比例不断增大时，假定轻型机与重型机的比例相同，且同时减少。3种机型所占比例的变化反映到跑道容量SPN模型中，即是参数λ的变化。机型的比例变化在SPN模型中与λ1、λ2以及λ3的数值有关，同时当机型的比例发生变化时还会对两条跑道的航空器平均占用时间产生影响，即λ16、λ17也相应的发生了变化，具体数据如表7所示。

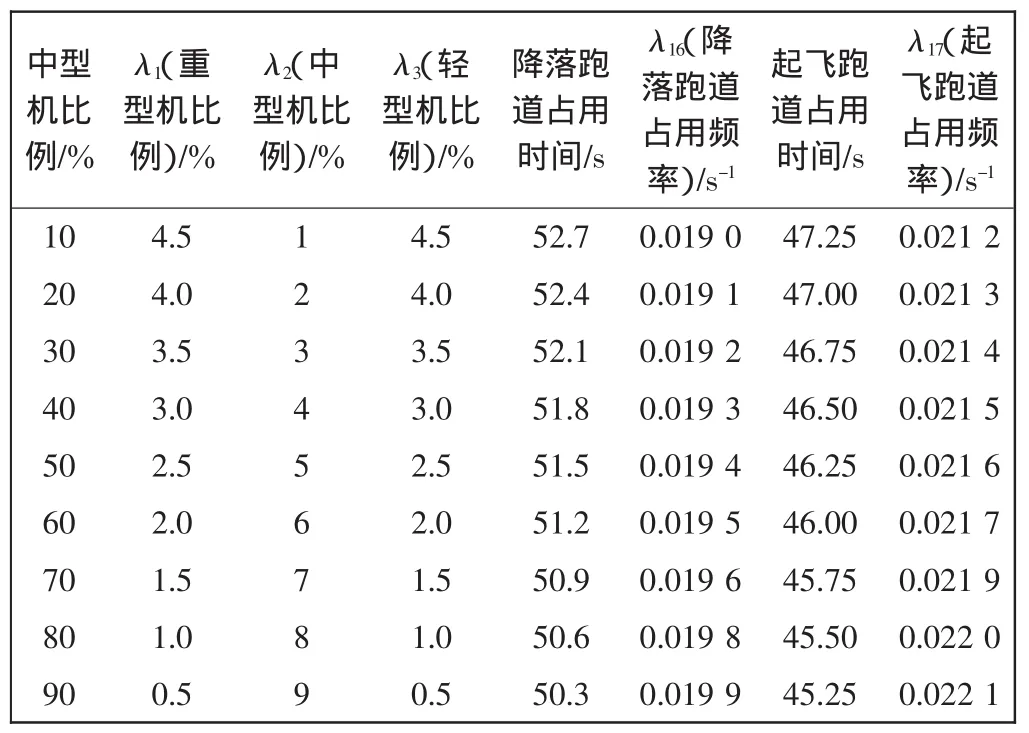
表7 中型机比例变化对λ的影响Tab.7 Effects of medium aircraft proportion change to λ

其它参数不变，将 λ1、λ2、λ3、λ16、λ17分别取表中数值时，代入式（2）中，计算出在中型机所占比例变化时对跑道容量的影响，如表8所示。

表8中的中型机变化对跑道容量变化的影响趋势如图4所示。

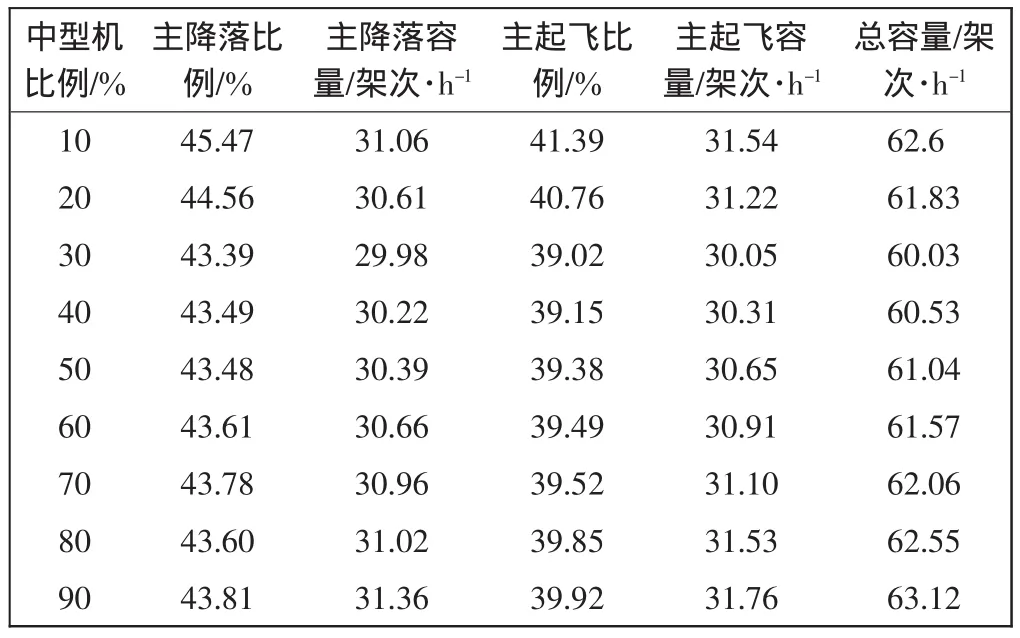
表8 中型机所占比例对跑道容量的影响Tab.8 Effects of medium aircraft proportion to runway capacity

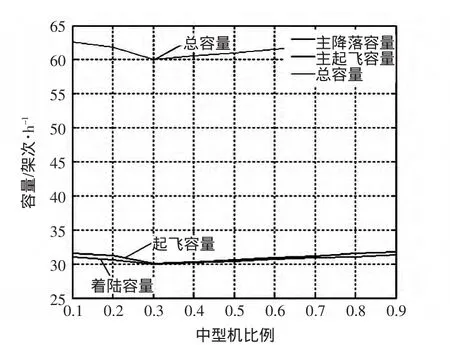
图4 容量与中型机比重曲线关系Fig.4 Curve relationship between runway capacity and medium aircraft proportion

由图4可看出，随着中型机所占比重的不断增大，重型机以及轻型机的比重不断减少。近距平行跑道的总容量曲线是呈现先减后增的趋势。该趋势对实际运行有一定的参考意义。

5.3 五边航空器距跑道距离对跑道容量的影响

将五边航空器距落地跑道起始端的间隔取不同的数值，计算并分析随着距离的变化跑道容量的变化，此时，其它参数不发生变化，即起降比为1：1，交替起降，且跑道占用时间采用均值，主降落跑道平均占用时间为52 s，即λ16=0.019 2，主起飞跑道平均占用时间为46 s，即λ17=0.021 7。其他参数为1。具体计算结果如表9所示。

将表9中的数据生成示意图，以五边距落地跑道端距离为横轴、容量为纵轴，分别生成距离对主起飞容量、主降落容量以及总容量的影响曲线，如图5所示。

从表9和图5可以看出，五边航空器距落地跑道起始端的距离越远，连续降落的飞机间隔就越大，相对的跑道容量就越小。五边航空器距落地跑道起始端的距离一定时，由于假定起降比为1：1，所以主降落和主起飞跑道的容量几乎是相同的，而由于跑道占用时间不同，跑道的利用率却不相同。图中可以看出，随着距离的增大，跑道容量迅速的减少。因此在实际的容量评估中应对评估范围加以明确的界定，否则得到的结果不是唯一。

表9 五边航空器距落地跑道端的距离Tab.9 Distance between traffic circuit and threshold

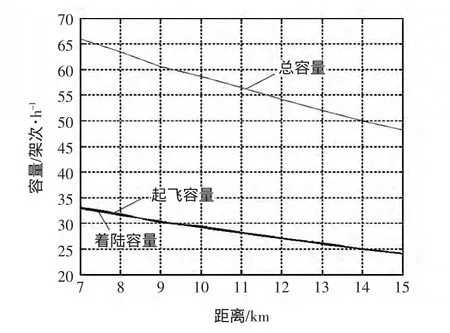
图5 五边航空器距落地跑道起始端的距离对跑道容量的影响Fig.5 Effects of distance between traffic circuit and threshold to runway capacity

6 结语

本文根据近距跑道的进离港运行情况，建立交替起降运行模式下的近距跑道随机Petri网模型，同构出模型的马尔科夫链，得到系统的状态转移概率矩阵和稳态概率表达式，进一步建立跑道容量的数学模型。在此基础之上，通过对模型中关键参数的调整，研究了中型机的比例对跑道容量的影响以及五边航空器距落地跑道起始端的距离对跑道容量的影响。本文所建模型可复用性强，参数调整更为灵活，对跑道容量的评估与分析具有一定的指导意义。

[1]胡明华，刘 松，苏兰根.基于统计分析的单跑道容量估计模型研究[J].数据采集与处理，2000，15（1）：74-77.

[2]骆慈孟.论空域规划空管体制与飞行安全[J].空中交通管理，1997，3（5）：17-20.

[3]《新航行系统》编辑委员会.新航行系统概论[M].北京：中国民航出版社，1997：257-281.

[4]王 维，李 伟.机场近距平行跑道一起一降模式下的容量计算[J].中国民航大学学报，2009，27（3）：20-22.

[5]CAO YIHUA，CHEN YONG，ZHOU YONG.Studies of capacity estimation of the airport with two parallel runways[J].Aeronautical Journal，2005，109（1098）：395-401.

[6]中国民用航空总局.平行跑道同时仪表运行管理规定[EB/OL].（2004-06-26）[2013-03-06].http://www.caac.gov.cn.

[7]中国民用航空总局.中国民用航空空中交通管理规则[EB/OL].（2000-01-05）[2013-03-06].http://www.caac.gov.cn.

[8]林 闯.随机Petri网和系统性能分析[M].北京：清华大学出版社，1999.

[9]罗继亮，邹慧莉.基于随机Petri网的车辆交通系统仿真与建模[J].系统仿真学报，2007，19（S1）：248-250.

[10]重庆江北国际机场近距平行跑道管制运行规程[Z].民航重庆空管分局，2002.