基于Benford法则的GDP数据可靠性分析

摘要：本文利用Benford定律并结合统计检验的方法，以四川省GDP相关数据为例，对我国地区统计数据质量的可靠性进行了研究。

关键词：Benford法则 GDP数据 可靠性

1 统计数据质量及可靠性的界定

质量是一个哲学概念，它是一个多维的立体的概念，具有相对性。随着人们质量观念的变化，人们逐步认识到质量不仅包括产品的使用性能，还包括需求客户对产品的满足程度，它成了一个内涵丰富的综合性概念。不同社会组织机构、不同用户、不同时期会有不同的质量标准和要求。同样，统计数据作为统计工作的产品，对统计数据质量内涵的认识也逐渐发生了变化。

过去认为统计数据质量就是统计数据的准确性，即统计数值与目标特征真实数值的接近程度或一致程度。而现在对统计数据质量的理解则由过去的单标准变成多标准、多层次的综合概念，具体要求的标准更多了，比如要求准确、适用、及时、可比、可取和客观等多具体标准。

可靠性是一个数理概念，是质量范畴的小概念，主要用来刻画统计数据质量标准之一的统计数据准确性的标尺，也就是对实际数据与真值之间的误差进行评估。评估数据质量可靠性的方法有很多，如经验分布检验、统计指标之间的逻辑检验、相对指标的相关分析、计量模型评价等。

2 Benford定律

我们知道，在社会经济统计领域很多统计总体的个体标志值在理论上服从某一特定的统计分布。鉴于此，通过对统计总体中的各个个体标志值进行特定的统计分布检验，可以初步判断出各个个体的标志值是否正常、可信。为此，笔者选择了Benford定律对四川省GDP相关数据进行可靠性检验。

Benford定律是自然数字的一种内在规律，其含义是指假设在样本空间足够大的情况下，第一位数字为1到9之间的数字发生的概率具有一定规律，越小的数字出现的比率越高，其中1为第一位数字出现的概率达0.3，2为第一位数字出现的概率为0.17-0.19，以此类推，8或9为第一数字出现的概念仅有0.05左右。

该定律的主要奠基人Frank Benford对人口出生率、死亡率、物理和化学常数、素数数字等各种现象进行统计分析后发现，由度量单位制获得的数据都符合Benford定律，即自然数1到9的使用频率，公式为：

F（d）=log[1+[1/d]] d=1，2，3……，9

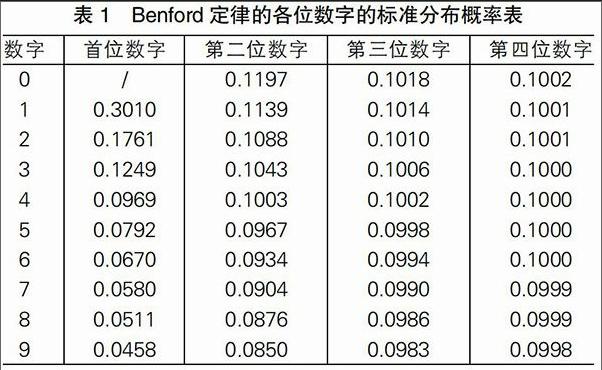
应该指出的是，利用Benford定律必须保证研究的数据无序且未人为修饰。该定律不但适用于第一位数字，也可用于第二位、第三位数字。在采用Benford定律，由公式计算得到的各位数字的标准分布概率，如表1结果所示：

表1 Benford定律的各位数字的标准分布概率表

■

此外，Benford定律也遵从大数法则和中心极限定理，基于文章篇幅的原因，这里就不一一证明。

3 基于Benford定律的四川省GDP统计数据实证分析

考虑到Benford定律在应用时候遵从的条件，如果我们所研究的数据样本存在人为加工处理，则该数据样本不符合该定律。所以对数据样本进行质量评估过程中，利用Benford定律进行分析，来检验数据的真实与否，是可信的。国内研究对Benford定律的应用主要集中在财务审计对上市公司的研究领域，很少有利用其对地区统计数据质量做实证研究分析。为此，本文选取了四川省1978-2011年的地区生产总值相关数据进行检验，判断四川统计数据质量是否可靠。

3.1 建立假设

假设四川省地区生产总值是可信的，根据Benford定律，GDP数据的前两位数的数字分布情况应该与Benford定律下的数字分布情况相同。为此，我们建立两个假设：

针对？字2检验，从整体出发，提出如下两个假设：

H1：四川省GDP数据的第一位数的出现次数与Benford定律下的随机分布相一致；

H2：四川省GDP数据的第二位数的出现次数与Benford定律下的随机分布相一致。

针对Z检验，从具体每个数字出现频率的期望值出发，提出如下两个假设：

H3：四川省GDP数据的第一位数中每个自然数（1，2，

3，……，9）出现频率与Benford法则下的频率相一致；

H4：四川省GDP数据的第二位数中每个自然数（0，1，

2，3，……，9）出现频率与Benford法则下的频率相一致。

3.2 数据说明

为了研究的深入，本文在考虑四川省GDP相关数据基础上，将四川省地区生产总值数据细分为第一、二、三产业三部分，并把同时期的人均地区生产总值数据纳入。数据均为历年四川省统计年鉴整理，具体数据略。

所采用的研究方法是用Excel软件分别统计1978年-

2011年四川省地区生产总值相关数据第一位数1至9这九个自然数和第二位数0至9这十个自然数出现的次数，并进行？字2检验和Z统计检验。

3.3 检验统计量

通过？字2拟合优度来评估出现的每个自然数出现的观测值和期望值之间的概率分布的拟合程度，以此来佐证四川省地区生产总值样本数据大小和总体上存在偏差；采用Z统计来评估各个自然数出现次数的差异性。两个检验公式如下所示：

？字2=∑[（ai-Ei）2/Ei]

式中ai是出现在观测值第一或第二位数的数字i的实际频数，Ei是出现在期望值中第一或第二位数的数字i的理论频数。

Zi=（P■-P■）/■

其中，P■为出现在观测值第一或第二位数的数字i的实际频率，P■为出现在期望值中第一或第二位数的数字i的理论频率，n为采集分析所用样本量。

当？字2越大，则表明研究数据总体上出现自然数的概率越小，更说明是人为修饰过的数据，则准确性很差；当Z绝对值越大的时候，该数字出现的频率与期望的频率偏离得越远。endprint

3.4 检验主要结果

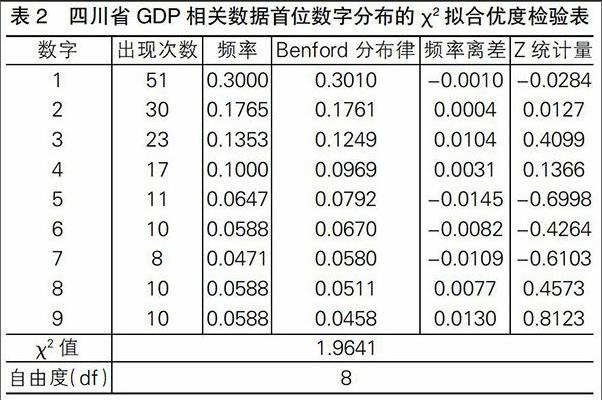
3.4.1 首先我们把1978年-2011年四川省GDP相关数据合并在一起，第一位数字分布偏差情况如下表2所示：

表2 四川省GDP相关数据首位数字分布的？字2拟合优度检验表

■

在0.05的显著性水平下，通过查表，我们可以得到 ？字2分布（df=8）的临界值为15.507。由上表2可知，首位数字分布的？字2统计值为1.9641，小于15.507，我们不能拒绝假设H1；同时，出现自然数Z统计量绝对值均小于1.96（0.05显著性水平下的Z值），我们应该接受假设H3。因此，在显著性水平（0.05）情况下，四川省GDP相关数据首位数字出现情况与期望频率没有明显不同。

由上面的检验结果，我们可以看出四川省GDP相关数据的第一位数字分布规律与Benford定律下的期望情况是一致的。所以，继续对四川省GDP相关数据的居第二位出现的自然数的分布采用相关理论进行检验。

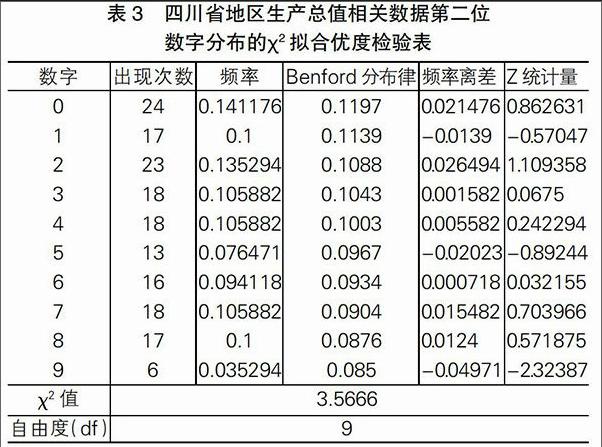
3.4.2 四川省GDP相关数据第二位数字分布的？字2拟合优度检验如下表3所示：

表3 四川省地区生产总值相关数据第二位

数字分布的？字2拟合优度检验表

■

在0.05的显著性水平下，通过查表，我们可以得到？字2 分布（df=9）的临界值为18.314。由表2可知，居第二位数字出现的频率服从分布的？字2统计值为3.5666，小于18.314，我们不能拒绝假设H2；从中我们还应该看出数字9的Z统计量绝对值大于1.96（0.05显著性水平下的Z值），我们应该接收假设H4。因此，在显著性水平（0.05）情况下，不能认为四川省GDP相关数据第二位数字的出现自然数频率与期望频率无差异性。

根据这一检验结果笔者认为，四川省GDP相关数据的第二位数字的分布规律与Benford定律下的期望规律不符合。

4 主要结论

本文通过Benford定律的应用并结合了统计检验的方法，对四川省GDP相关数据进行了可靠性分析。研究结果显示，四川省地区生产总值相关数据在首位数字分布上符合本福特法则，但在第二位数字分布上并不完全符合本福特法则，说明统计数据并不十分可靠。究其原因，可能有三：

其一，我们所研究的该样本数据被人工修改过；

其二，研究条件中样本量还不够大，研究的选择样本空间人为在选择时候就出现了选择性偏差，其结果就出现了统计误差；

其三，Benford定律的检验建立在数据真实的基础上，且需要受检验的数据满足具有稳定增长率的条件，这本身就是一个缺陷。

参考文献：

[1]傅德印，陶然.对政府统计数据质量成本的探讨[J].统计研究，2007（8）.

[2]东方杜奇.新时期统计数据质量可靠性研究[J].特区经济，2005（4）.

[3]斐辉儒，宋伟.我国统计数据质量体系存在的问题及解决思路[J].统计与决策，2006（4）.

作者简介：晏正春（1979-），湖南沅江人，成都信息工程学院统计学院教师，讲师，硕士研究生。endprint