基于冲击放电试验的电力电容器外壳振动预估方法

祝令瑜 汲胜昌 沈 琪 刘 源 刘 浩

（1.西安交通大学电气工程学院电力设备电气绝缘国家重点实验室 西安 710049 2.绍兴电力局 绍兴 312000）

1 引言

在特高压直流工程中，电容器装置中电容器数量多，流过的谐波电流大，导致其可听噪声污染问题日益突出[1-11]。虽然尚未制定电容器噪声计算的标准，但是近年来新建的直流工程招投标都已经对电容器噪声计算报告及噪声限值都提出了严格要求[12]。由于由电容器外壳振动速度计算电容器噪声的研究已经比较成熟，对电容器外壳振动预估方法的研究有着重要的工程意义和研究价值。

从20 世纪90 年代中期开始，很多关于电容器噪声振动特性和计算方法的研究已经开展。M.D.Cox 等人首先基于冲击力锤试验获取的传递函数计算了电流畸变情况下的电容器外壳振动[13]，但是当时仅针对频谱形式的归一化计算，并未涉及外壳振动的定量计算。Smede 等人建立了电容器装置1∶4模型，对电容器装置的噪声水平及噪声方向特性进行了研究，为装置结构设计提出了建议[14]。显然这种噪声研究方法耗时耗力并不经济。曹涛等人提出了比较精确的基于电容器外壳振动速度计算电容器噪声的方法[15]，但是没有给出外壳振动速度的计算方法。2008～2009 年，孙新波等人先后利用将每个电容器简化为点声源的计算方法和Kirchhoff 公式对滤波电容器装置的噪声声压级进行了估算[16,17]，但是这些计算方法也是以电容器外壳振动速度为基础的，没有解决准确预估电容器外壳振动速度的问题。2010 年魏浩征等人提出用测试比较法确定电容器噪声声功率，解决了电容器噪声试验中的测试方法问题[18]，却未涉及电容器噪声振动的计算方法。汲胜昌等人曾于2006 年提出了基于模态分析和冲击力锤试验的单台电容器和电容器装置的噪声计算方法[19,20]，也是目前最为广泛使用的电容器振动及噪声计算方法。然而，在冲击力锤试验中，冲击力仅仅作用在电容器外壳上，无法激发电容器内部元件的振动。因此，基于冲击力锤试验获取的传递函数也无法完整地反映电容器内部振动产生及传递的电气机械特性。

如前所述，尽管长期以来相关的研究工作已经开展了很多，但是仍然没有提出合理满意的电容器外壳振动计算方法。本文提出一种基于冲击放电试验的电容器外壳振动计算方法并进行验证。首先从电容器噪声产生机理出发提出了“机电联合频响函数”的概念，为基于冲击放电试验的电容器外壳振动计算方法提供了理论基础。然后描述了基于冲击放电试验的电容器外壳振动计算方法及测量电容器外壳振动的试验方法，并通过对预估结果与试验结果的比较说明预估方法的可行性。最后对本文提出的电容器外壳振动方法进行了讨论。

2 振动预估方法

通常在高压直流系统中使用的是罐式全膜电容器。电容器外壳一般是钢或不锈钢材料，顶部安装出线套管，内部是一个浸油的芯子元件包。芯子元件包由一系列串并联的电容器元件构成。电容器元件是由两片铝箔和塑料或纸膜卷绕压制而成的。当电压作用在电容器上，两铝箔电极带相异电荷，内部的塑料膜会受压紧静电力的作用。如果施加交流电压，电容器元件在交变静电力作用下会产生振动。电容器元件的振动经过内部电容器油及固定支撑结构的传递引起电容器外壳的振动[1]。

要准确地预估电容器外壳在实际运行工况下的振动情况，需要首先掌握电容器的机械电气特性并以数学的方式进行表达。本文首先给出机电联合频响函数的定义，用以描述电容器内部的机械电气特性。

2.1 “机电联合频响函数”的定义

假设电容器内部的机械系统是线性系统，则存在电容器外壳响应与静电力之间的线性系统，它可以用机械频响函数Hm(ω)进行描述，机械频响函数的定义式如下

式中，ω是振动角频率；V(ω)是频域的电容器外壳振动响应；F(ω)是频域的静电力。

根据已有分析，元件内部极板间静电力与施加在电容器上电压的平方成正比，即

式中，f(t)是极板间的静电力；K为比例系数；u(t)为施加在电容器上的电压。

因此，电容器外壳振动与电压平方之间的系统也是线性系统。本文使用包含电气机械特性的频响函数H(ω)用于描述该线性系统

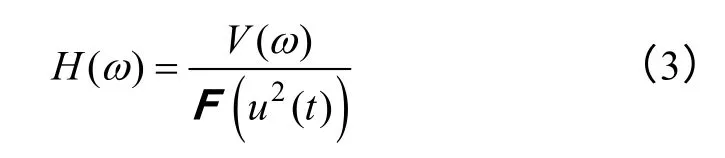
式中，F（u2(t)）为电容器电压平方 u2(t)的傅里叶变换。

2.2 机电联合频响函数的获取方法

实际直流系统中，流过电容器的最高频率电流为49次谐波电流[21]。由谐波电流导致的电容器外壳振动可以达到4 900Hz。为了获取宽频带内（50～5 000Hz）电容器的机械电气特性，本文使用冲击放电试验的方法获取机电联合频响函数。

冲击放电试验过程与电容器型式试验中的短路放电试验类似[22]，首先将电容器充电到一定电压，然后电容器经过一个小电阻放电，使得如图1 所示的电压作用在电容器上，电容器受到宽频的电场力激励作用。电容器放电的同时，测量电容器外壳各点的振动速度。利用机电联合频响函数的定义式（3）即可获取电容器的机电联合频响函数。

冲击放电试验中，电压的波形是一个下降沿（见图1）。显然，电压信号以及它的平方是时域无限的非周期信号，所以不能用FFT（快速傅里叶变换）直接对计算其离散傅里叶变换。本文对电压平方求微分将其转换为时域有限信号，再利用傅里叶变换的微分性质对电压平方信号进行频域的分析。

图1 冲击放电试验中的电压波形Fig.1 Voltage waveform of capacitor in the impulse discharge test

利用高等数学知识，电压平方对时间的微分可以化为

由电路基本理论，电容器的电流是其电压的微分与电容量的乘积，即

将式（5）代入式（4），可得

由傅里叶变换的微分性质，若 x(t)的傅里叶变换为 X(ω)，则dx (t)(dt)的傅里叶变换为jω X(ω)。

因此，u2(t)的傅里叶变换为

ui为时域有限信号，所以可以用FFT 对其进行离散傅里叶变换，进而得到电压平方的离散傅里叶变换。

与冲击力锤试验不同，在冲击放电试验中，电容器外壳的振动是由芯子元件受电流激励振动引起的，所以由此试验得到的机电联合频响函数反映了电容器内部振动产生和传递的全部机械电气特性。

2.3 基于机电联合频响函数的振动预估

获取了机电联合频响函数，根据电容器工况即可对电容器外壳振动进行预估。在振动预估问题中，通常已知流过电容器的各次电流，记为I(ω)，以及电容器的电容量C。

对于电容器，频域电压与电流满足

利用傅里叶逆变换可以获取时域的电容器电压

假设获取的电容器机电联合频响函数为H(ω)，则在电压激励下电容器外壳振动速度响应为

3 验证试验设计

本文对一台实际电容器在两组电流（见表1）下的振动进行预估和实测，通过比较证明基于冲击放电试验的电容器振动预估方法的可行性。试品电容器型号为BAMr12—417—1W，额定电压为12kV，额定容量417kvar。实测电容量为9.46μF。电容器的结构和尺寸如图2 所示。本文称外壳上安装套管的面为顶面，与顶面相对的面为底面，其余面根据宽度不同分别称为宽侧面和窄侧面。

图2 试品电容器结构与尺寸Fig.2 Configuration and size of the test capacitor

表1 施加的电容器电流Tab.1 Applied capacitor currents

3.1 电容器外壳振动的预估

首先利用冲击放电试验获取电容器的机电联合频响函数。冲击放电的试验电路如图3 所示。图中T1为调压器，T2为试验变压器，VD为高压硅堆，C为试品电容器，S为分流器，G为触发球隙，R为调波电阻。试验变压器与高压硅堆组成半波整流电路。首先用整流电路将电容器充电到U0，然后触发球隙导通，电容器经过分流器和调波电阻放电。分流器用于测量流过被试电容器的电流。试验前调整调波电阻的阻值，使得冲击放电发生电路处于过阻尼状态，以确保电流在考察频带内（50～5 000Hz）有足够的幅值。在电容器放电的同时，使用激光测振仪测量电容器外壳的振动速度。振动测量系统如图4 所示。激光测振仪利用外差干涉仪原理测量电容器外壳表面法线方向的振动速度，测量时激光光束方向与电容器外壳表面垂直。振动速度信号由示波器采集。主要设备参数如下：

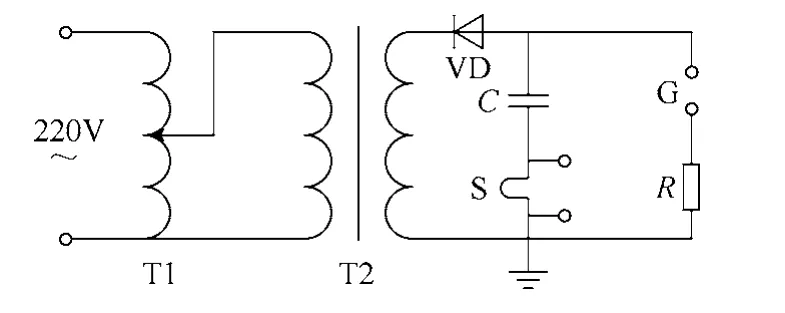
图3 冲击放电试验电路Fig.3 Experimental circuit of the impulse discharge test

图4 振动测量系统Fig.4 Vibration measurement system

（1）分流器，阻值为0.001 84Ω。

（2）激光测振仪，便携式数字激光测振仪PDV—100 由德国Polytec GmbH 公司制造，工作频带0～22kHz，传输时延约为1ms。量程有20mm/s、100mm/s和 500mm/s 三个档位可选。低通滤波器的截止（0.1dB）频率有1kHz、5kHz 和22kHz 三个档位可选。

（3）示波器，使用美国泰克公司的DPO4054，带宽为500MHz，采样率为5GS/s，记录长度为20M。

试验时，电容器采用与实际工程中相同的方式立卧安装。在电容器外壳上选择若干均匀分布的振动测点。对电容器重复冲击放电，同时依次测量电容器外壳各测点的振动速度。

设测量第j个点振动时，流过电容器的电流为ij(t)，电容器上的电压uj(t)计算为

测得的振动速度设为vj(t)，则由式（3）和式（7），可得第j个点的机电联合频响函数为

在已知电容器工况和电容器参数并获取了机电联合频响函数的情况下，电容器外壳各点的振动可由式（8）～式（10）估算。

3.2 电容器振动实测

电容器振动实测试验系统由主电路和振动测量部分组成，如图5 所示。主电路由谐波源非晶变压器和电容器组成。谐波源输出电压40～340V，连续可调，额定输出电流176A，额定输出功率60kV·A，频率调节范围50～1 250Hz，可以输出最多9 种谐波叠加的混合波。非晶合金变压器在高频下仍具有低铁损和低激磁电流，不会产生铁心饱和的问题。非晶变压器的额定容量为 60kV·A，有两组额定电压为15 000/340V，额定电流为2/176.5A 的绕组。振动测量系统、电容器安装方式及振动测点布置与冲击放电试验相同（见图4）。

图5 实测振动试验系统Fig.5 Test system for vibration measurement

4 预估结果分析

4.1 冲击放电试验结果分析

冲击放电试验中流过电容器的电流如图6 所示，波形接近8/20μs 的冲击电流波形。在0～5 000Hz频率范围内，ui 在各频率下的幅值基本相等，说明电容器受到了理想的宽频激励，归一化的ui 幅频曲线如图7 所示。在利用式（12）计算机电联合频响函数时，分母即 2F（uj(t)ij(t)）的幅值在各频率下差别不大是获得精确结果的基础，因此本文电流波形的选取是合理的。

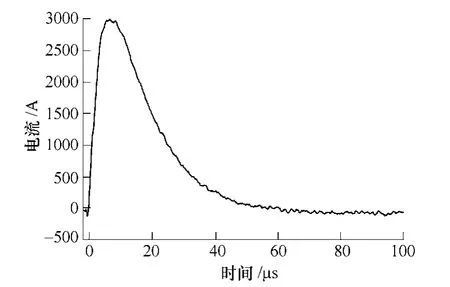
图6 冲击放电试验中电流波形Fig.6 Current waveform of capacitor in impulse discharge test

图7 归一化的冲击放电试验中电压电流乘积幅频曲线Fig.7 Normalized amplitude-frequency curve of the product of current and voltage in the impulse discharge test

本文所测电容器宽侧面、窄侧面和底面的平均机电联合频响函数的幅频曲线如图8 所示。

图8 电容器各表面平均机电联合频响函数Fig.8 Average electro-mechanical frequency response functions of surfaces of capacitor tank

从幅频曲线可以看出，宽侧面和窄侧面的振动响应类似，且与底面的振动响应有很大不同。侧面的机电联合频响函数幅值在低频段（小于3 000Hz）很小，而在高于3 000Hz 的高频段有很多谐振峰。而底面的联合频响函数幅值在低于3 000Hz 的低频段很大，在高于3 000Hz 的高频段很小。底面机电联合频响函数的峰值约为侧面频响函数峰值的4～6倍，也印证了底面是电容器振动的主振面[1]。

4.2 预估与实测振动比较

给电容器施加单频率电流激励时，电容器两端电压的平方为电流频率两倍的单频正弦信号；给电容器施加的多频率叠加电流时，电容器两端电压的平方含有电流频率的两倍项、各频率差频项及和频项。电容器外壳振动与电容器两端电压平方成线性关系。因此，在电流1 激励下，电容器外壳振动应为100Hz正弦波，在电流 2 激励下，电容器外壳振动含有50Hz，100Hz，150Hz 及200Hz 项。信号底面中点在两种电流激励下的振动波形如图9 和图10 所示。

利用式（8）～式（10）及试验获取的机电联合频响函数，估算电容器外壳各点的振动速度。通过比较底面中点处的计算结果与测量结果验证本文所提出的计算方法。底面中点处的机电联合频响函数如图11 所示。为了反映该预估方法在电容器噪声计算中的准确性，衡量预估结果与实测结果的差异度，引入振动速度级。在利用振动速度计算电容器外壳辐射噪声时，需要先计算振动速度级Lv，其定义为

图9 电容器外壳底面中点在电流1 激励下的振动波形Fig.9 Vibration waveform of middle point of bottom surface under the excitation of current 1

图10 电容器外壳底面中点在电流2 激励下的振动波形Fig.10 Vibration waveform of middle point of bottom surface under the excitation of current 2

图11 电容器外壳底面中点机电联合频响函数Fig.11 Electro-mechanical frequency response function at the middle point of bottom surface

式中，v为振动速度；v0=5×10-8m/s为基准速度。

对实测结果进行频谱分析，频谱间隔为50Hz，得到预估与实测振动频谱比较图如图12 和图13 所示。受实测条件影响，实测频谱中含有除理论频率点之外的其他频率含量。但是主要频率点的幅值均比其他频率点幅值大20dB 以上，说明本文所测结果在频率含量方面与理论分析一致。在电流1 激励下，预测结果与实测结果在100Hz 处的振动速度级仅相差0.6dB，满足标准对测量不确定度的要求[23]，说明本文所提方法能准确预测单频率激励下的电容器外壳振动。在电流2 激励的条件下，预测频谱与实测频谱形状相接近（见图13）。各频率下的振动速度级见表2。预估振动速度除在50Hz 处与实测结果相差 4.2dB 外，其他频率点处误差小于1dB，且各频率含量的大小关系一致，说明本文提出的振动预估方法能准确预估电容器外壳在多频率激励下振动频谱。振动速度满足频域的能量叠加，即

图12 底面中点在电流1 激励下预估与实测振动频谱比较Fig.12 Comparison of predicted and measured vibration spectrum of middle point of bottom surface under the excitation of current 1

叠加后预估的振动速度级为58.5dB，实测的振动速度级为58.6dB，仅相差0.1dB，本文提出的预估方法具有很高的精度。

图13 底面中点在电流2 激励下预估与实测振动频谱比较Fig.13 Comparison of predicted and measured vibration spectrum of middle point of bottom surface under the excitation of current 2

表2 电流2 激励下底面中点各频率的振动速度级Tab.2 Vibration velocity level of each frequency of bottom surface under the excitation of current 2

5 讨论

本文基于冲击放电试验获取的机电联合频响函数能准确地反映电容器从受电激励产生振动到振动传递到外壳的全部过程，包含了电容器的机械及电气特性，验证试验结果也说明了振动预估方法能预测电容器在单频率和多频率电源激励下的振动频谱，且具有很高的精度。在个别频率点（如50Hz），预估结果相差相对较大，误差可能来自于冲击放电试验中的工频干扰。

使用电激励测量外壳振动方法有效地解决了预估电容器外壳在特定工况下振动情况的问题。然而获取机电联合频响函数的试验中施加电激励的形式还有待进一步探讨。本文为了获取相对宽频的激励，使用了冲击放电的试验方法。在该试验中，电容器先充电然后快速放电，电容器承受快速释放的力。这种阶跃型的力低频含量相对较高，有利于反映低频特性。另一方面，冲击放电中大电流可能产生较大的电动力，与稳态下电容器受静电力激励振动的情况并不完全相符。使用扫频方法可以有助于减弱高低频之间的差异，在更宽的频带内获取电容器的机械电气特性，而且单频正弦的激励与稳态下电容器振动时所受激励更为接近，有望获得更理想的预估效果。对施加电激励形式的研究将是下一步的研究重点。

6 结论

本文提出并讨论了一种新型的电容器外壳振动预估方法。将外壳振动速度与电压平方的频域比定义为机电联合频响函数，并给出了利用冲击放电试验获取机电联合频响函数的方法。基于机电联合频响函数，阐述了特定激励下的电容器外壳振动速度的计算方法。通过将预估计算结果与实测电容器外壳振动进行比较说明了本文所提方法对可行性与准确性。在单频和多频两种激励下，基于机电联合频响函数的方法都能准确预估电容器外壳振动的频谱，且具有很高的精度（小于1dB）。因此，本文所提直流换流站中的电容器外壳振动预估方法准确可行。

冲击放电试验使用了电激励的方法测试电容器的电气机械特性，与实际中电容器所受激励形式相似，所以基于冲击放电试验获取的机电联合频响函数能够全面地反映电容器在振动产生过程中的全部特性。机电联合频响函数建立了电激励与电容器外壳振动响应之间的联系，而模态分析无法反映电激励的过程。因此，本文提出的基于机电联合频响函数的预估方法有望使换流站电容器噪声预估方法取得重要改进。

[1]CIGRE,No.202 W.G 14.26,HVDC stations audible noise[R].Apr.2002,Tech.Rep.

[2]李文毅,孙竹森,肖安全,等.三沪直流工程换流站噪声治理[J].中国电力.2008,41(1):32-35.Li Wenyi,Sun Zhusen,Xiao Anquan.Noise treatment in Three Gorges—Shanghai ± 500kV DC transmission converter stations[J].Electric Power,2008,41(1):32-35.

[3]杨一鸣,章旭雯.特高压直流换流站设备的降噪措施[J].高电压技术,2006,32(9):149-152.Yang Yiming,Zhang Xuwen.Study on noise reduce for equipment at UHVDC converter station[J].High Voltage Engineering,2006,32(9):149-152.

[4]韩辉,吴桂芳,瞿雪弟,等.我国±500kV 换流站设备可听噪声的测量分析及降噪措施[J].电网技术,2008,32(2):38-41.Han Hui,Wu Guifang,Qu Xuedi,et al.Measurement and analysis of audible noise bringing about by equipment in domestic ±500kV converter stations and noise reduction measures[J].Power System Technology,2008,32(2):38-41.

[5]俞敦辉.±800kV 特高压换流站噪声控制探讨[J].电力建设,2009,30(3):13-16.Yu Dunhui.Discussion on ±800kV UHV converter station noise control[J].Electric Power Construction,2009,30(3):13-16.

[6]张劲松.高压直流换流站噪声综合治理研究[J].电力建设,2007,28(8):14-16.Zhang Jinsong.Research on comprehensive treatment of HVDC converter station noise[J].Electric Power Construction,2007,28(8):14-16.

[7]高湛,胡小龙.蔡家冲(宜都)换流站噪声冶理研究和实践[J].电力建设,2007,28(3):13-16.Gao Zhan,Hu Xiaolong.Research and practice of noise control for Caijiachong(Yidu)converter station[J].Electric Power Construction,2007,28(3):13-16.

[8]高湛,胡小龙,李华.高岭背靠背换流站噪声控制方案研究[J].电力建设,2008,29(8):22-24.Gao Zhan,Hu Xiaolong,Li Hua.Study on noise control scheme for Gaoling back-to-back converter station[J].Electric Power Construction,2008,29(8):22-24.

[9]孙竹森,俞敦耀.华新换流站噪声控制探讨[J].电力建设,2007,28(11):10-13.Sun Zhusen,Yu Dunyao.Discussion on noise control at Huaxin converter station[J].Electric Power Construction,2007,28(11):10-13.

[10]中国电力科学研究院.三峡－常州±500kV 直流输电工程可听噪声测试报告[R].2003.

[11]中国电力科学研究院.三峡－广州±500kV 直流输电工程可听噪声测试报告[R].2004.

[12]北京网联直流输电工程咨询有限责任公司.“三峡—上海直流输电项目”技术规范[R].北京:2005.

[13]Cox M D,Guan H H.Vibration and audible noise of capacitors subjected to non-sinusoidal waveforms[J].IEEE Transactions on Power Delivery,1994,9(2):856-862.

[14]Smede J,Johansson C G,Winroth O,et al.Design of HVDC converter stations with respect to audible noise requirements[J].IEEE Transactions on Power Delivery,1995,10(2):747-758.

[15]曹涛,汲胜昌,吴鹏,等.基于振动信号的电容器噪声水平计算方法[J].电工技术学报,2010,25(6):172-177.Cao Tao,Ji Shengchang,Wu Peng,et al.Calculation method of noise level for capacitor based on vibration signal[J].Transactions of China Electrotechnical Society,2010,25(6):172-177.

[16]孙新波,陈花玲,姚成.电容器装置噪声水平的估算方法[J].电力电容器与无功补偿,2008,29(1):13-16.Sun Xinbo,Chen Hualing,Yao Cheng.Estimating method for noise level of capacitor installations[J].Power Capacitor &Reactive Power Compensation,2008,29(1):13-16.

[17]孙新波,吴九汇,陈花玲.Kirchhoff 公式在电容器装置噪声水平预估中的应用[J].噪声与振动控制,2009,29(5):140-175.Sun Xinbo,Wu Jiuhui,Chen Hualing.Application of kirchhoff formula in prediction of noise level of capacitor installation[J].Noise and Vibration Control,2009,29(5):140-175.

[18]魏浩征,李志远,黎小林,等.高压直流换流站电容器的声功率的确定方法[J].高压电器,2010,46(1):68-75.Wei Haozheng,Li Zhiyuan,Li Xiaolin,et al.Acoustic power determination of capacitors in HVDC converter station[J].High Voltage Apparatus,2010,46(1):68-75.

[19]汲胜昌,寇小括,李彦明.换流站中电容器装置噪声水平计算方法的研究[J].中国电机工程学报,2006,26(3):112-118.Ji Shengchang,Kou Xiaokuo,Li Yanming.Study on the calculation method of noise level for capacitor installation at converter station[J].Proceedings of the CSEE,2006,26(3):112-118.

[20]Ji S,Wu P,Zhang Q,et al.Study on the noise-level calculation method for capacitor stacks in HVDC converter station[J].IEEE Transactions on Power Delivery,2010,25(3):1866-1873.

[21]赵畹君.高压直流输电工程技术[M].北京:中国电力出版社,2004.

[22]IEC 60871—1—1997 Shunt capacitors for a.c.power systems having a rated voltage above 1 000V—Part 1:General-performance,testing and rating-safety requirements-Guide for installation and operation[S].1979.

[23]GB/T 6882—2008 声学 声压法测定噪声源声功率级:消声室和半消声室精密法[S].2008.