综合考虑可靠性与经济性的电力变压器检修方案优选

张镱议 廖瑞金 杨丽君 孟繁津 李金忠 程涣超

（1.重庆大学输配电装备及系统安全与新技术国家重点实验室 重庆 400030 2.中国电力科学研究院 北京 100192）

1 引言

随着电网规模和电压等级的扩大和市场经济的引入，电力企业对输变电设备的安全、经济运行提出了更高的要求。电力变压器作为输变电设备中的关键设备之一，其运行的可靠性与经济性直接影响电力系统的安全与稳定[1]。因此，如何制定合理的变压器维修策略，兼顾变压器运行的可靠性和经济性，成为了电力企业的核心问题之一。

近年来，国内外对变压器维修策略的研究主要集中在变压器的状态检修上。其中包括基于变压器状态评估的状态检修[2-5]、基于变压器可靠性评价的状态检修[6,7]与基于全寿命周期成本的检修[8-10]。文献[2]提出了一种基于模糊证据的变压器状态评价方法，但是并没有考虑到检修的经济性因素。文献[7]提出了一种基于马尔科夫模型的变压器可靠性评价方法，但是没有能够综合考虑经济性，制定出比较合理的检修准则。文献[8]提出了一种变压器全寿命周期成本的计算方法，虽考虑了经济性，但是没有深入分析变压器的故障机理进行模型的搭建。国家电网公司生产技术部于2008 年发布了《国家电网公司设备状态检修规章制度和技术标准汇编》[11]，在此汇编中简述了输变电设备风险评估的方法，但是该方法稍显简单。

究竟能否找出一种能综合考虑变压器健康状态、变压器可靠性与变压器运行维修成本的检修策略制定方法呢？因此，本文试图构造一种能够综合考虑变压器运行可靠性与经济性的状态检修策略优选模型。从变压器的内部机理出发，通过寻找变压器健康状态与故障率的关系，建立变压器检修对故障率影响的模型。并采用粒子群方法对构建的变压器检修决策优选模型进行检修策略优选，旨在找到一个可靠性与经济性综合最优的检修决策结果。最后，通过实例研究验证所构建模型的有效性和合理性，为变压器的检修优化提供一条新思路。

2 变压器运行可靠性模型的确定

2.1 绝缘健康状态评估指标选取

根据专家经验以及相关规程[11-14]选取了一些易于测量且对变压器各绝缘状态影响较大的特征量作为评估指标。

变压器绝缘状态评估指标体系如图1 所示。由于不同的指标对绝缘状态的影响程度不同，因此如何科学地确定评价体系的权重显得尤其重要。本文采用改进AHP 法来确定变压器各因素和指标的权重[2]，由此确定的各指标权重值如表1 所示。

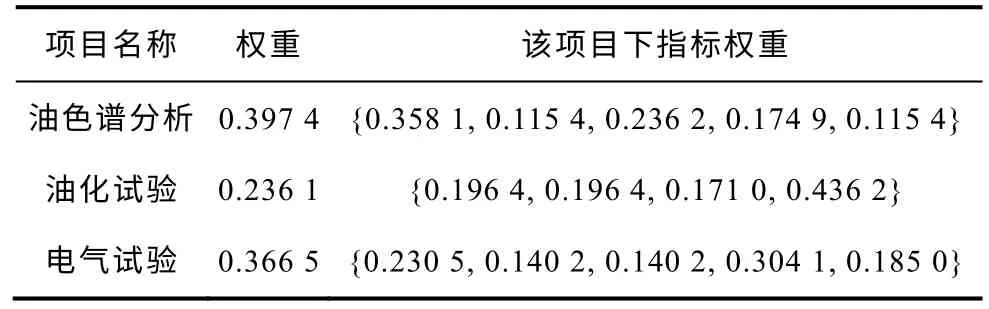
表1 评估指标的权重Tab.1 Weights of assessing indices

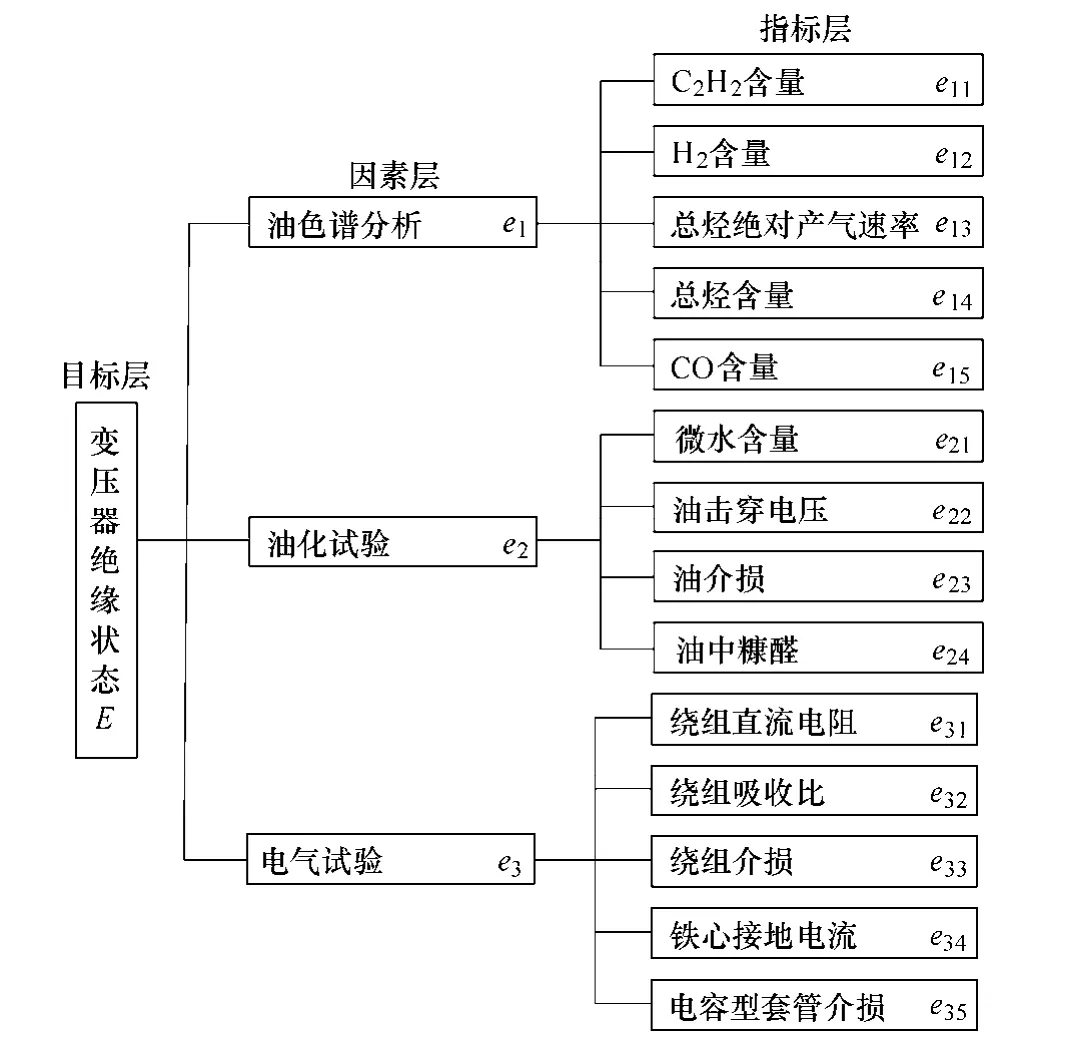
图1 变压器绝缘评价体系Fig.1 Assessing index system of transformer insulation condition

2.2 综合健康状态修正因子

变压器的综合健康状态不仅与其绝缘状态有关，而且与其运行环境情况和检修记录有关。其中运行环境情况包括运行年限、平均寿命、运行环境和负荷等方面；检修记录包括家族缺陷、近区短路、冷却系统情况、缺陷记录、故障记录和局放情况等方面。由于这些因素直接影响到变压器的老化速率，如图2 所示，本文将这些因素分别组合，形成运行环境情况修正因子a1和检修记录修正因子a2。各指标与修正系数之间的关系如表2 所示。如若其中某个指标缺省，则令该指标的修正系数为1。

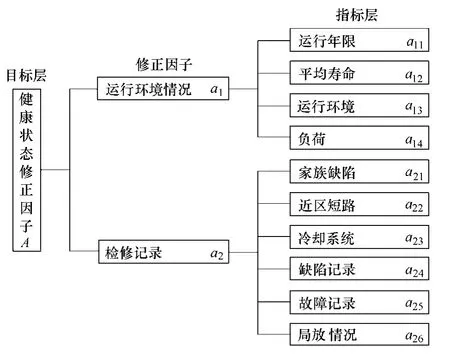
图2 健康状态修正因子体系Fig.2 Assessing index system of the corrected parameters

表2 指标与修正系数之间的关系Tab.2 The relationship between the indexes and the corrected parameters

2.3 变压器故障率的计算

变压器的综合健康指数不但与变压器绝缘状态有关，而且与综合状态修正因子有关。变压器的综合健康指数可以通过下面的式子进行计算。

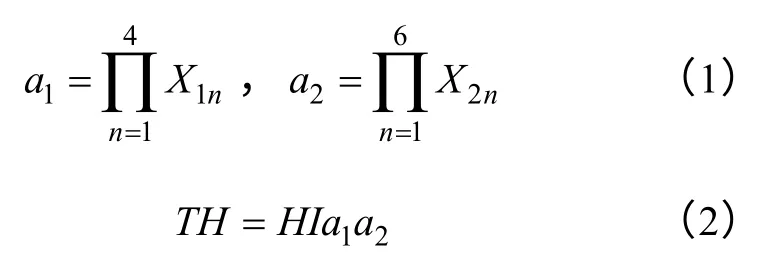
式中，TH是变压器的综合健康指数，取值范围为[0,100]，分值越小，变压器的健康状态越好，如果其计算结果大于100，则归算为100；HI为变压器的绝缘状态指数；a1和a2分别为运行环境情况和检修记录修正因子。

另外，为了构建健康指数、故障率、以及实际役龄的关系，本文引入一个健康指数计算公式，如式（3）所示。该式是根据设备老化原理，描述设备状态随时间变化的一个经验公式。该公式已广泛应用于电力设备的状态评估中[16]。

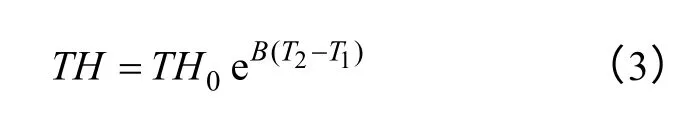
式中，TH是综合健康指数；TH0是综合健康指数的投运初始值，经统计与专家经验可设为5；B为老化系数；T1为新设备投运年份；T2为所要计算综合健康指数的年份。

若能确定初始健康值和寿命结束健康值就可以估算变压器的老化系数B。假设变压器初始投运健康值为5；定义Texp为变压器预期寿命，预计变压器运行Texp年后，其故障率明显上升，此时的健康指数为75。Texp可以通过变压器的设计寿命、运行环境情况修正因子及检修记录修正因子的关系获得。它们之间的关系如下式所示

式中，Texp为变压器的期望寿命；Tdes为变压器的设计寿命，本文中Tdes=30；a1和a2分别为运行环境情况修正因子和检修记录修正因子。

由此可以推出老化系数B 的估算值

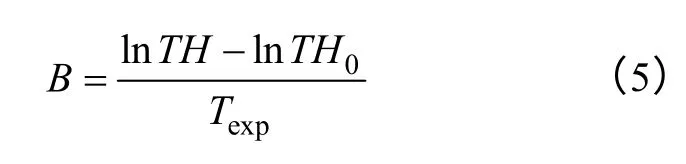
经式（5）可得B 的取值。得到经验公式后便可根据式（6）大略估算变压器在此条件下继续运行的未来健康值。由于综合考虑到大小修因素的影响，根据实际役龄和等效役龄的关系，将式（3）修正为

式中，ΔT'为变压器的等效役龄。

考虑到模糊理论在变压器绝缘状态评价中的应用效果较为良好，能够较为准确的描述绝缘评价中的模糊性和不确定性。因此，本文拟采用模糊理论进行HI 的确定。具体步骤如下：

（1）归一化指标值，通过模糊隶属函数取得指标的隶属矩阵。

（2）采用模糊融合方法对权重信息和隶属函数信息进行加权计算，得到三个因素层的评判矩阵。

（3）将这三个评判矩阵进行模糊信息融合，最终获得一个反映变压器绝缘状态的评判矩阵。

（4）构建绝缘状态评判矩阵与变压器绝缘健康指数的关系。并通过式（7），将评判矩阵的信息转化成一个0～100 的健康指数值，进行绝缘状态指数的确定。

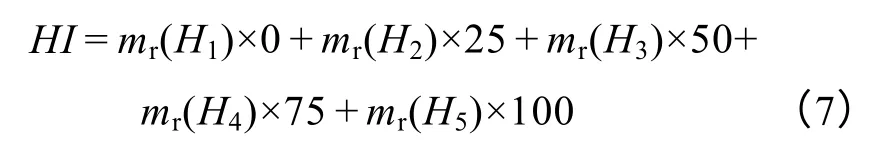
式中，HI是绝缘健康指数，它的取值范围是[0，100]，它的值为0 时说明它的绝缘状态很好，未遭受任何的绝缘老化；它的值为100 时说明它的绝缘状态非常严重，绝缘已经到达老化末期；mr为最终计算的评判矩阵；mr(Hn)为评判矩阵支持每个等级的概率。

（5）查阅历史数据，根据表2，通过式（1）进行综合健康状态修正因子的确定。

（6）根据式（2）进行综合健康指数的确定。

（7）根据式（8）中健康指数与故障率的关系构建变压器的可靠性模型[17]。

式中，λ为设备故障率；K为比例系数；C为曲率系数；TH为变压器的综合状态指数。

可根据文献[17]中表1 的数据，通过反演法（如式（9）所示），利用下式计算出C 和K 的值。最终可确定参数K=0.011 2，C=0.045 1。

式中，λ为设备故障率；l为故障变压器台数；L为变压器总台数，n=1，2，…，10，共分成10 类；Ln为第n 类变压器的台数；THn为根据n 的分类，为对应TH 分值上下限的平均值。

2.4 检修对变压器故障率的影响

根据工程经验，当变压器健康指数较低时，变压器状态较好，维修对健康指数的恢复作用较小。随着变压器绝缘的劣化，变压器健康指数变大，变压器健康状态变差，维修对健康指数的恢复作用变大。当变压器劣化到一定程度时，维修对健康指数的恢复作用则趋于稳定。根据以上经验，可以合理假设变压器健康指数恢复值与变压器的健康指数的关系可以用分段函数来描述。在变压器的健康指数为[5,10]时进行小修，变压器的健康指数恢复值为0；健康指数为[50,100]时进行小修，变压器的健康指数恢复值为 h1（本文中取 h1=6）。同理假设在变压器的健康指数为[5,10]时进行大修，变压器的健康指数恢复值为0；健康指数为[75,100]时进行大修，变压器的健康指数恢复值为h2（本文中取h2=25）。当变压器健康指数为75 时，采取大修检修措施后，健康指数与故障率的关系如图 3所示。

图3 大修后综合健康指数与故障率的关系Fig.3 The relationship between the health index and the fault ratio after major maintenance

由此可以拟合出不同健康状态下，小修、大修情况后，健康指数和健康指数恢复值的关系，分别如式（10）和式（11）所示。

因此，当变压器小修时，等效役龄变短，变压器的健康指数减少H1分，进而使故障率相对应的降低，但降低的故障率不会低于起始故障率。

合理假设小修成本与变压器的健康指数呈现出线性的关系，当变压器的健康指数越高时，状态就越差，需要采取的措施和测量也就越多。按专家经验把小修成本定义为

合理假设当110kV、220kV、500kV 变压器健康指数为5 时，小修费用分别为1 万元，2 万元，3万元；健康指数为50 时，小修费用分别为10 万元、20 万元、28 万元；则可由此拟合出不同电压等级变压器小修的健康指数与成本关系曲线。

当变压器大修时，等效役龄缩短，变压器的健康指数减少H2分，进而使故障率相对应的降低，但降低的故障率不会低于起始故障率。由于变压器大修所需的时间一致，试验项目也一致，因此合理假设变压器大修成本为一个定值。根据专家经验，110kV、220kV、500kV 变压器大修取值分别为购置费的6%[18]：48 万元、100 万元、360 万元（变压器的购置费用分别为800 万元、1 700 万元、6 000 万元）。当变压器更换时，变压器的健康指数恢复到5 分，故障率回落到起始故障率。更换成本为变压器购买成本和安装成本之和，也可以假设为一个定值。根据专家经验，110kV、220kV、500kV 变压器更换取值分别为：900 万元、2 000 万元、7 000万元。

3 基于变压器风险评估的检修策略优选

3.1 变压器风险体系的构建

作为关键枢纽设备的变压器，一旦其发生故障，很容易使得与其连接的电气设备发生一系列的连锁反应，甚至发生故障，进而产生不良的社会影响。因此，对于变压器的风险评估，本文拟采用下式进行确定

式中，Risk 指的是变压器的风险值，单位是元；POTF是变压器的故障发生概率，由第2.3 节确定；LOTF是变压器发生故障后的经济损失。

本文中LOTF 主要包括系统风险、故障修复成本、人员生产、环境影响等因素。

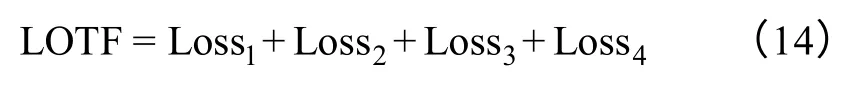
从系统风险的角度出发，变压器故障的时间不同，其造成的经济损失也就不同。因此，为了粗略量化变压器的经济损失，本文将变压器故障分为一般性、严重性和灾难性故障。其定义如下：

一般性故障——一些不需要紧急修复的故障，可以在24h 内修复的故障。

严重性故障——一些较为紧急的故障，需要2～10 天的修复时间。

灾难性故障——一些紧急的故障，需要10 天以上的修复时间。

采用统计数据，分别将一般性、严重性和灾难性故障的故障概率r1、r2、r3确定为64.2%、32.1%、3.7%[19]。

假定一旦变压器发生故障，则切除负荷造成的经济损失如下式所示。

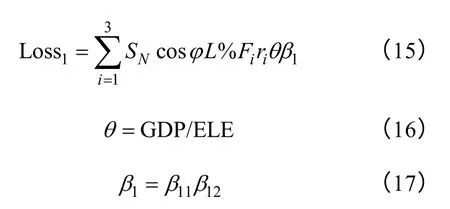
式中，SN为变压器的容量；cosφ是平均功率因数，本文中cosφ=0.9；L%为变压器的负载率；Fi(i=1,2,3)分别表示变压器在不同故障下切除负荷的几率，分别取值分别为1%、5%、10%，故障时间的取值分别为24h、120h、240h；θ为单位电量风险值，2012年中国GDP为49.591 万亿元[20]，2012 年用电量是519 322MW·h[21]，因此，θ＝10 472.1 元/(MW·h)；β1为系统风险的修正系数，主要包括变电站的重要性β11、变压器负荷的重要性β12，它们的取值如表3所示。

表3 系统风险修正系数的选择Tab.3 Corrected parameters of system risk

故障修复成本包括材料费用、人工费用、设备费用等费用。平均故障成本的估算如下：

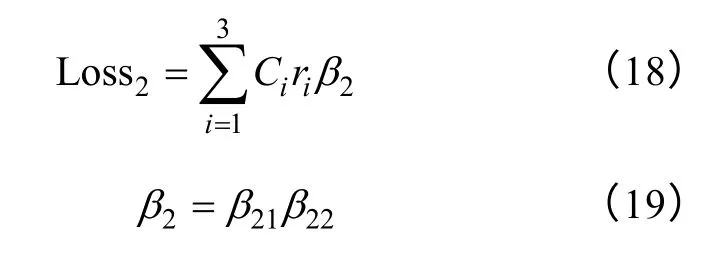
故障概率r1、r2、r3分别为64.2%、32.1%、3.7%；Ci(i=1，2，3)分别表示变压器在不同故障下的修复成本。根据专家经验，C1情况下，110kV、220kV、500kV 取值分别为1 万元、2 万元、3 万元；C2情况下分别为10 万元、20 万元、28 万元；C3情况下，取值分别为180 万元、500 万元、800 万元。B2为修复成本的修正系数，主要包括产地β21、变压器的检修环境β22，它们的取值如表4 所示。

表4 修复成本修正系数的选择Tab.4 Corrected parameters of repair cost

人员安全风险主要是指故障造成的安全事故。本文中按轻伤、重伤、人员死亡三个等级来划分风险的严重程度。可以由下式进行计算。

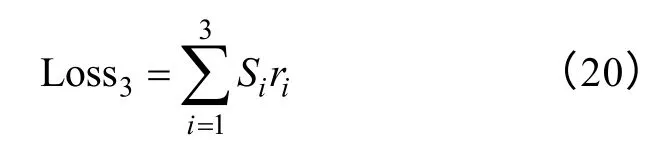
Si(i=1，2，3)分别表示变压器在不同故障下事故成本，分别取值分别为2 万元、500 万元、5 000 万元，发生人员伤亡的概率分别取值为1%、0.5%、0.1%。

环境风险指的是变压器发生故障后对环境造成污染的风险。由于变压器故障的环境污染主要由变压器油泄漏、二氧化碳的释放以及变压器故障起火时释放的有毒气体。其风险值可以由下式确定。

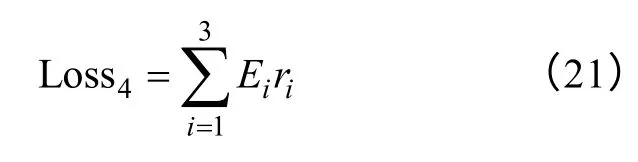
Ei(i=1，2，3)分别表示变压器在不同故障下的平均环境成本，分别取值为1 万元、10 万元、20 万元。

3.2 变压器检修优化模型的建立

本模型的目标在于保证变压器安全运行的同时，利用尽可能少的检修成本，确保变压器的故障率在可接受的范围内，获得最大的风险收益。

由此变压器的检修优化问题转化为求下式的最小化问题。

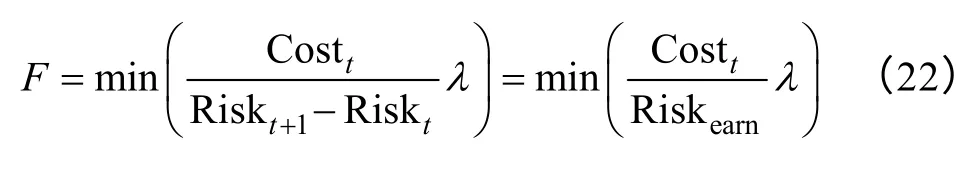
式中，F为最小化的函数表达式；Costt为维修所需要的成本；Riskt+1是t+1 时刻检修后的风险值；Riskt是变压器在t 时刻的风险值；λ为检修后的故障率；Riskearn是风险收益。

约束条件有：

（1）变压器投运五年内大修一次，若无故障大修后至少每十年实施一次大修。变压器至少每一年进行一次小修。

（2）当变压器的健康指数处于[5,50]范围时，认为变压器的状态尚佳，建议对变压器进行小修或者大修。当变压器的健康指数处于（50,90]范围时，认为变压器的健康状态有迅速下降的趋势，当尽快安排相应的大修或者更换的检修措施。当变压器的健康指数处于（90,100]范围时，认为变压器绝缘老化已经非常严重，进入故障频发期，建议进行更换。

（3）当变压器已经存在较严重故障时，当进行大修或者更换。

3.3 基于粒子群优化的检修方式选择

由于粒子群优化算法有较强的全局寻优能力，本文拟采用粒子群优化的方法来解决变压器的检修优化问题，确定变压器的最佳检修方式和最佳检修时间。其算法流程如图4 所示。

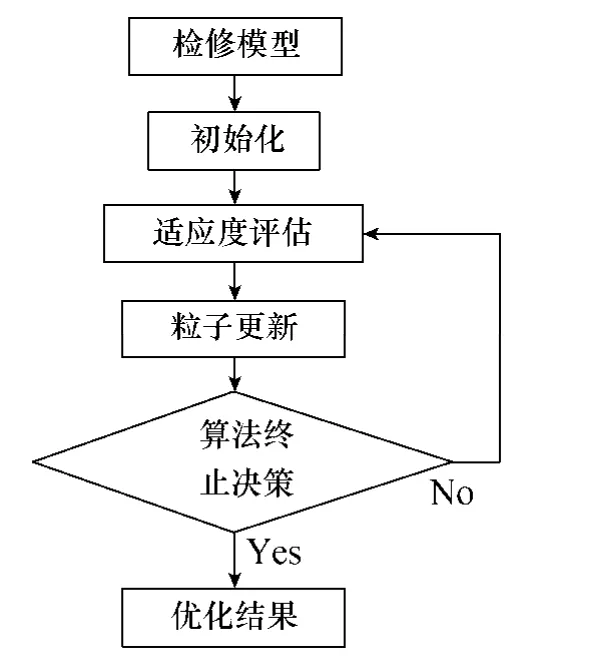
图4 检修优化流程图Fig.4 Flowchart of maintenance optimization

主要实现步骤如下[22]：

（1）检修方式的初选。根据变压器的健康指数以及3.2 节描述的约束条件，构建相应的检修优化模型。

（2）PSO 初始化。针对不同的检修模型，进行PSO 初始化。在定义的d（d=1）维空间中，随机产生初始粒子X1,…,Xi,…,XS，组成种群X，令种群个数Population=24；随机产生种群的初始速度和位移；设定粒子速度变化的最大值vmax=0.2rang（TH），加速常数值c1=2，c2=2 和粒子的最大进化代数Tmax=2 000。

（3）适应度评估。确定种群中各个粒子在搜索空间上的初始适应度值，并比较各个粒子适应度值与个体极值pid，如果当前值比pid更优，则置pid为当前值，并记录个体极值的位置。比较在种群中所有粒子适应度值与全局极值pgd，如若当前值比pgd更优，则置pgd为当前值，并记录下全局极值所在的位置。

（4）粒子更新。更新粒子的速度和位置，以寻求最优的全局解。

（5）算法终止判断。检查PSO 进程结束条件是否满足，即如果寻优达到最大进化代数Tmax或评价值小于给定精度eg=10-25，则结束寻优过程；否则，转到步骤（3）。

（6）检修方式选择及其检修时间选择。根据不同检修方式下的最优结果，对变压器的检修方案进行确定。例如：当变压器的健康指数处于[5,50]范围时，则计算对变压器进行小修和大修的最佳检修方式和最佳检修时间，根据对比结果选择最终检修方式和最终检修时间。当变压器的健康指数处于（50,90]范围时，应当计算变压器大修和更换的最佳检修方式和最佳检修时间，根据对比结果选择最终检修方式和最终检修时间。当变压器的健康指数处于（90,100]范围时，则应计算对变压器进行更换的最佳检修方式和最佳检修时间。

4 实例研究

某变电站1998 年投运的220kV，150MV·A 的室外电力变压器，其型号为OSFPS—150000/500，平均负载率为41%，其年最高温度为33.5oC。色谱记录如表5 所示，预防性试验数据如表6 所示。

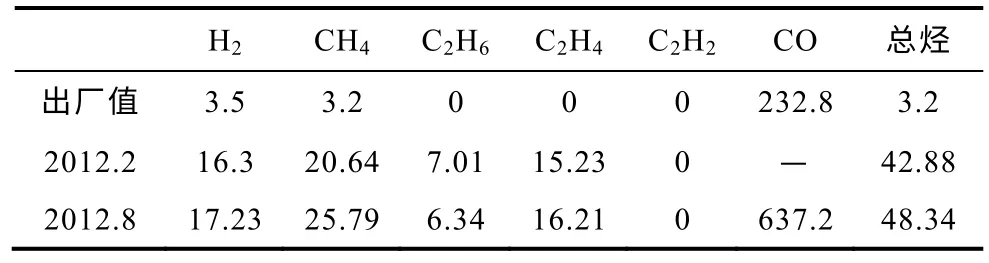
表5 油色谱分析数据Tab.5 DGA data of the transformer （×10-6）

表6 预防性试验数据Tab.6 Preventive test data of the transformer

根据文献[2]确定各个指标的相对劣化度：E1=(e11, e12, e13, e14, e15)=(0.346 5,0.093 7,0.210 0,0.324 2,0.322 3)；E2=(e21, e22, e23, e24)=(0.25,0.190 5,0.173 1,0.065)；E3=(e31, e32, e33, e34, e35)=(0.105 8,0.306 0,0.306 0,0.320 0,0.471 4)；结合表1 中的权重信息，根据表7 中的隶属度计算结果，采用模糊矩阵计算方法，可得变压器的健康评判矩阵 E=(0.248 9,0.657 4,0.093 7,0,0)。通过式（7）进行健康指数变换，可得该变压器的健康指数为21.121 2。此外根据相关的信息，可得变压器的修正因子除a11=1.02、a13=1.02、a14=0.969 4 外，其他修正因子都等于1，其中a23、a24、a25都取缺省值，根据式（1）可得a1=1.008 5、a2=1。根据式（2），可确定该变压器的综合健康指数TH为21.30。另外，根据式（3）～式（6），可以确定该变压器的老化系数B=0.091 0，等效役龄ΔT=15.93 年，根据检修约束条件1，可得该变压器小修和大修的时间范围分别是[15.93 16.93]和[15.93 25.93]，根据式（3）和式（6），其所对应的健康指数值分别为[21.30 23.32]和[21.30 52.91]。根据式（15）～式（21），可得Loss1=2.098 0×109，Loss2=2.620 4×105，Loss3=1.000 3×104，Loss4=4.592×104。根据式（14），可得该变压器发生故障后的经济损失 LOTF=2.098 4×109。根据式（10）、式（12）、式（22）以及式（11）、式（22）分别构建变压器在小修和大修方式下的最优化函数

表7 隶属度的计算值Tab.7 Result of membership degrees

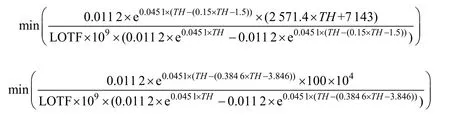
另外，本文还给出了该变压器更换的最优化目标函数

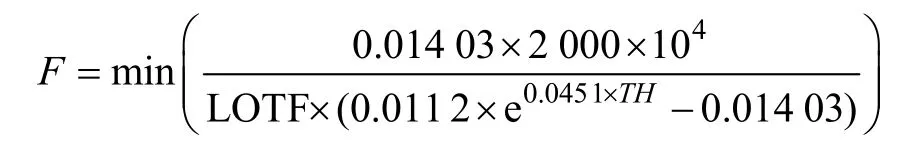
根据3.3 节所述的检修优化流程，小修和大修的寻优的健康指数范围分别为[21.30 23.33]和[21.30 52.92]，采用PSO 优化后可得小修和大修的最优检修时间分别为一年后和十年后，其对应的最优化值分别为3.390×10-4和4.312×10-4，其PSO 寻优结果分别显示于图5 和图6 中。最终可确定两者之间的最小值为最佳检修方案，可得该变压器的最佳检修方式为小修，建议一年之后实行。

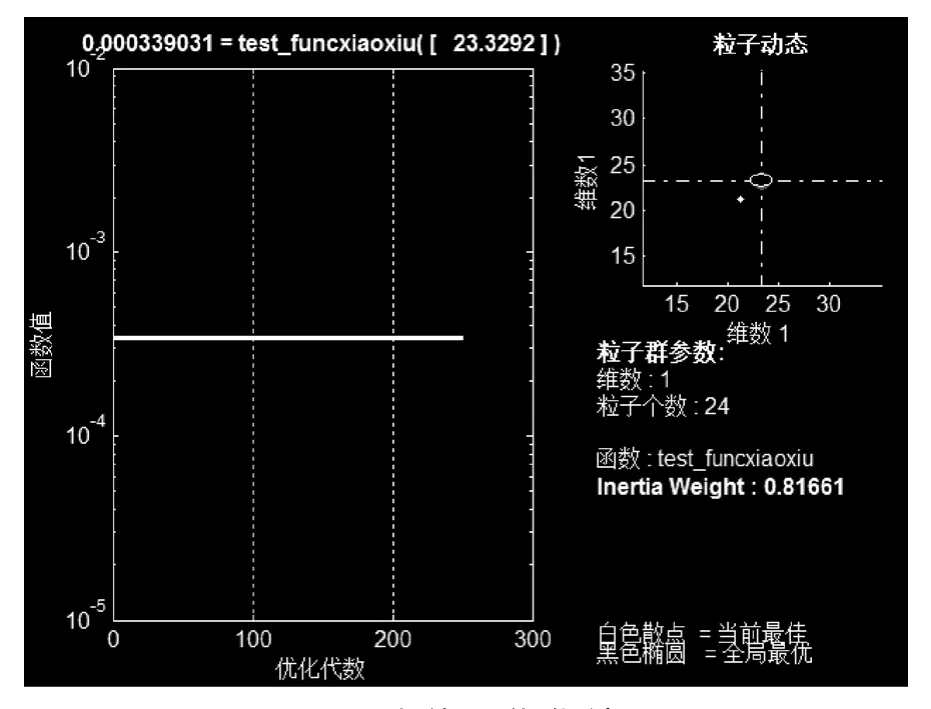
图5 小修最优化结果Fig.5 Maintenance result of minor repair

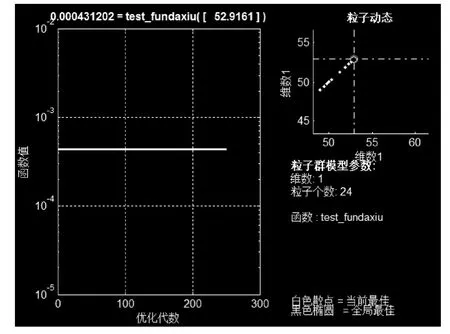
图6 大修最优化结果Fig.6 Maintenance result of overhaul

根据其等效役龄ΔT′=15.93 可知，变压器的实际运行时间和等效役龄相差不大，可以推算出该变压器基本处于正常劣化的过程中。另外根据变压器的健康指数为21.30，尚处于一个较为正常的状态，并不需要在近期安排检修，因此将其检修时间安排在一年后是比较合理的。实际情况是实施本检修方式以来，直到2013 年5 月为止，该变压器运行状态良好，并未发生故障，可见之前的检修决策是比较合理的，这也验证了本文方法的有效性。

5 结论

本文根据相关规程和专家经验，在构建变压器绝缘评价体系的基础上，建立了一种综合考虑健康状态修正因子的变压器综合健康指数评价方法；根据建立的健康指数与变压器故障率的关系，通过量化不同故障率下的变压器运行风险，构建了合理的检修模型，提出了一种综合考虑变压器经济性和技术性的状态检修优选方法。并基于粒子群方法对检修变压器的检修方式和检修时间进行了方案的确定。经实例验证表明，该方法有效合理，可以为变压器的检修优化提供一条新思路。

但是，由于变压器的状态检修和全寿命周期管理尚处于研究初级阶段，难以收集大量的变压器检修前后的预防性试验数据，因此难以精细地刻画变压器不同检修方式在不同运行年限下对变压器健康指数的影响。此外，本文在经济性风险评估上还存在一定的主观经验性，下一步将寻求其优化的结果。

[1]廖瑞金,杨丽君,郑含博,等.电力变压器油纸绝缘热老化研究综述[J].电工技术学报,2012,27(05):1-12.Liao Ruijin,Yang Lijun,Zheng Hanbo,et al.Reviews on oil-paper insulation thermal aging in power transformers[J].Transactions of China Electrotechnical Society,2012,27(05):1-12.

[2]Liao Ruijin,Zheng Hanbo,Grzybowski Stanislaw,et al.An integrated decision-making model for condition assessment of power transformers using fuzzy approach and evidential reasoning[J].IEEE Transactions on Power Delivery,2011,26(2):1111-1118.

[3]张镱议,廖瑞金,杨丽君,等.基于云理论的电力变压器绝缘状态评估方法[J].电工技术学报,2012,27(5):13-20.Zhang Yiyi,Liao Ruijin,Yang Lijun,et al.An assessment method for insulation condition of power transformer based upon cloud model[J].Transactions of China Electrotechnical Society,2012,27(5):13-20.

[4]郑蕊蕊,赵继印,吴宝春,等.基于加权灰靶理论的电力变压器绝缘状态分级评估方法[J].电工技术学报,2008,23(8):60-66.Zheng Ruirui,Zhao Jiyin,Wu Baochun,et al.Method for insulative condition classification evaluation of power transformers based on weight coefficient grey target theory[J].Transactions of China Electrotechnical Society,2008,23(8):60-66.

[5]王一,王慧芳,张亮,等.基于效用和成本的状态检修维修方式选择研究[J].电力系统保护与控制,2010,38(19):39-45.Wang Yi,Wang Huifang,Zhang Liang,et al.Research on maintenance type selection with CBM technology based on effectiveness and cost analysis[J].Power System Protection and Control,2010,38(19):39-45.

[6]孙鹏,陈绍辉,张彩庆.基于Marquardt 法参数估计的变电设备寿命周期故障率评估[J].电力系统保护与控制,2012,40(01):85-90.Sun Peng,Chen Shaohui,Zhang Caiqing.Assessment of failure rate for substation equipment life cycle based on Marquardt parameter estimation method[J].Power System Protection and Control,2012,40(01):85-90.

[7]廖瑞金,肖中男,巩晶,等.应用马尔科夫模型评估电力变压器可靠性[J].高电压技术,2010,36(2):322-328.Liao RuiJin,Xiao ZhongNan,Gong Jing,et al.Markov model for reliability assessment of power transformers[J].High Voltage Engineering,2010,36(2):322-328.

[8]宋宛净,姚建刚,汪觉恒,等.全寿命周期成本理论在主变压器选择中的应用[J].电力系统及其自动化学报,2012,24(06):111-116.Song WanJing,Yao Jiangang,Wang Jueheng,et al.Application of life cycle cost theory in main transformer selection[J].Proceedings of the Chinese Society of Universities for Electric Power System and its Automation,2012,24(06):111-116.

[9]崔新奇,尹来宾,范春菊,等.变电站改造中变压器全生命周期费用(LCC)模型的研究[J].电力系统保护与控制,2010,38(07):69-73.Cui Xinqi,Yin Laibin,Fan Chunju,et al.Study of LCC for power transformer in modification of transformer substation[J].Power System Protection and Control,2010,38(07):69-73.

[10]罗晓初,李乐,魏志连,等.全寿命周期成本理论在配电变压器改造投资决策中的应用[J].电网技术,2011,35(02):207-211.Luo Xiaochu,Li Le,Wei Zhilian,et al.Applications of life cycle cost theory in decision-making of investment for distribution transformers renovation[J].Power System Technology,2011,35(02):207-211.

[11]国家电网公司生产技术部.国家电网公司设备状态检修规章制度和技术标准汇编[M].北京:中国电力出版社,2008.

[12]国家质量监督检测监督总局.变压器油中溶解气体分析和判断导则GB/T 7252—2001[S].北京:中国标准出版社,2001.

[13]中华人民共和国电力工业部.电力设备预防性试验规程 DL/596—1996[S].北京:中国标准出版社,1996.

[14]IEEE Guide for the interpretation of gases generated in oil-immersed transformers,IEEE Std.C57.104—2008[S].New York:IEEE Press,2009.

[15]张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004.

[16]Hu Ghes D,Dennis G,Walker J,et al.Condition based risk management(CBRM)enabling asset condition information to be central to corporate decision making[C].Proceedings of the 1st World Congress on Engineering Asset Management,Gold Coast,Australia,2006,1212-1217.

[17]潘乐真,张焰,俞国勤,等.状态检修决策中的电气设备故障率推算[J].电力自动化设备,2010,30(02):91-94.Pan Lezhen,Zhang Yan,Yu Guoqin,et al.Prediction of electrical equipment failure rate for conditionbased maintenance decision-making[J].Electric Power Automation Equipment,2010,30(02):91-94.

[18]夏成军,邱桂华,黄冬燕,等.电力变压器全寿命周期成本模型及灵敏度分析[J].华东电力,2012,40(01):26-30.Xia Chengjun,Qiu Guihua,Huang Dongyan,et al.Life cycle cost model and sensitivity analysis of power transformer[J].East China Electric Power,2012,40(01):26-30.

[19]许珂.大型电力变压器故障实例统计分析[J].华章,2008(10):162-163.Xu Ke.Statistical analysis of fault cases of power transformer[J].Hua Zhang,2008(10):162-163.

[20]中华人民共和国国家统计局.2012 年国内生产总值(GDP)初步核算情况[OL].http://www.stats.gov.cn/tjfx/jdfx/t20130119_402867380.htm.北京,2013.

[21]中华人民共和国国家能源局.国家能源局发布2012年全社会用电量[OL].http://www.nea.gov.cn/2013-01/14/c_132100340.htm.北京,2013.

[22]纪震,廖惠连,吴青华.粒子群算法及应用[M].北京:科学出版社,2009.