基于流固耦合理论的泥页岩井壁稳定性分析

2014-11-23黄桃蒲晓林

石油天然气学报 2014年10期

黄桃，蒲晓林

罗霄，于浩（油气藏地质及开发工程国家重点实验室（西南石油大学），四川成都 610500）

徐生江（中石油新疆油田分公司工程技术研究院，新疆克拉玛依 834000）

石油作为世界上重要的能源资源，已经成为各个行业不可或缺的宝贵资源。而钻探作业是提高开采效率的重要环节，钻探作业中比较棘手的问题就是钻泥页岩地层，因为这样的地层在与水基钻井液相互作用的过程中经常会发生诸如溢流、漏失、坍塌、井眼缩颈、压差卡钻等井壁失稳的复杂事故，这会严重地影响钻井效率，增加成本［1，2］。怎么准确预测钻探过程中潜在的风险，而且快速地指导现场工人对事故的判断，提高勘探开发效益，取决于对这个多场耦合问题精确的描述和快速的计算仿真。

钻井工程理论和实践证明，在钻遇泥页岩地层时，由于水基泥浆在与泥页岩的浸泡过程中，井壁形成一层弱渗透泥饼，钻井液滤液在正压差作用下，向地层渗流，由于弱渗透层的封堵作用，滤液缓慢向地层侵入，侵入深度是时间的函数，导致地层含水量和孔隙压力增加，并由此导致水化膨胀应变，在钻垂直井段，水化膨胀应变在垂向方向上难以释放，故在水平方向产生巨大的膨胀应力，由此引发井壁失稳。关于这方面的理论建立，Yew和Chenevert［3～5］在文献中有详细的描述；关于膨胀应力与吸水量关系研究石油大学邓金根等［6，7］做了大量的研究工作，并给出了泥页岩膨胀应变与吸水量的关系式。

笔者基于前人的研究成果，综合考虑地层温度、渗流、水化对井壁稳定的影响，利用Comsol Multiphysics多物理场耦合分析软件对钻泥页岩地层过程中井壁稳定性进行分析，并考虑岩石弹塑性非线性响应，为实际钻井提供依据。

1 模型的建立及求解

泥页岩井壁稳定分析的模型主要包括考虑膨胀应力和温度应力，以及孔隙压力的弹塑性力学模型［8，9］，考虑滤液渗透的渗流力学模型。

模型建立基于如下假设：①地层为各向同性均质线弹性模型；②井眼横截面是圆形的；③地层无限大，拟分析二维平面应变问题。

1.1 流固耦合变形方程

考虑水化应力、温度条件下多场流固耦合方程由下式给出［10］：

式中：σij，j为应力张量，MPa；δij为Kronecker函数；α为Biot系数，1；p为孔隙压力，MPa；fi为体载，MPa。

水化后应力本构关系由增量弹塑性方程描述，其增量形式为：

式中：｛dσij｝为有效应力张量，MPa；［De］为弹性矩阵；为弹性应变张量的增量，1；dεij为塑性区全应变增量，1；为塑性应变增量，1；由温度产生的应变增量，1；由含水率产生的应变增量，1。

采用相关联的流动规则由下式给出：

式中：g为塑性势函数；dλ为比例因子，比例因子的求取则要从屈服准则和硬化规律中推导；理想塑性条件下可以将g近似看成屈服函数F。屈服准则采用适合岩石和土壤的Drucker－Prager准则，其表达式如下：

式中：a、k为材料参数，与材料内聚力和内摩擦角相关，可以根据偏平面上Drucker－Prager和Mohr－Coulomb准则位置的相互关系，得到多种表达式；随着泥页岩水化的进行，F函数也将发生变化，其实质是F也是含水量w的函数，当F＞0时证明井壁没有发生坍塌破坏，若F＜0时则根据准则可判断井壁发生失稳；I1为应力张量第一不变量；J2为应力偏张量第二不变量。

I1、J2的表达式分别如下：

式中：σ1、σ2、σ3分别为3个主应力分量，MPa。

同时，用一加载函数Φ（σij，H）来建立硬化定律的一般形式，理想塑性条件下Φ可以近似取作F，其中H为硬化参量。

水化膨胀应变增量和温度应变增量由下式计算：

式中：k1、k2为材料系数，1；am为热膨胀系数，1；δw为含水增量，1；δT为温度增量，K。

泥页岩水化导致强度降低，进而导致泥页岩强度参数变化，其随含水率w变化由下式给出：

式中：E为弹性模量，MPa；μ为泊松比，1；c为内聚力，MPa；cB为泥页岩含水率为wB时内黏聚力，MPa；φ为内摩擦角，（°）；φB为泥页岩含水率为wB时内摩擦角，（°）。

进行上述岩土弹塑性力学方程的耦合计算还必须给出含水率w的分布，工程上常采用热扩散方程来比拟水扩散方程，从而得到含水分布所必须满足的条件控制方程：

边界条件为：

式中：C为泥页岩吸水扩散系数，具体数值由实验测出［6，7］；ws为井壁达到饱和时的含水率，1；w0为原始地层含水率，1；r、rw为井径，m。

1.2 渗流方程

根据多孔介质渗流力学理论，钻井液在钻井液柱正压差作用下，往地层渗流，从而引起地层近井壁处孔隙压力增加，孔隙压力增加引起近井壁处应变发生变化，该过程是渗流力和弹性力相互作用的流固耦合过程，渗流过程中孔隙压力所满足的连续性方程由下式给出［8］：

式中：K为多孔介质绝对渗透率，mD；μ为滤液黏度，Pa·s；ρ为流体的密度，g／cm3；为多孔介质孔隙度，1；p为孔隙压力，kPa；t为时间，h；Cf为流体的压缩系数，kPa－1。

假设固体骨架仅发生孔隙变形，则孔隙度与变形量有如下关系：

式中：εv为体积应变，εv＝εx＋εy＋εz，1；0为初始孔隙度，1。传热耦合中，多孔介质传热方程由下式给出：

式中：CM为多孔介质的比热容，J／（kg·K）；λM为热传导系数，W／（m·K）。

1.3 模型的求解

模拟采用了岩土力学模块和多孔弹性模块、多孔介质传热以及自定义方程模块，耦合部分手动添加；利用Comsol平台，在求解多场问题时可以在模块之间互相调用，自定义一些函数或者参数供计算时调用。该方法非常适合科学研究，采用有限单元法数值求解，对线性和非线性问题都适用［9，10］。

2 计算实例

2.1 数值模型及边界条件

以某泥页岩井段为例，埋藏深度2855m，根据弹塑性力学有限元理论，考虑无限大地层二维平面，由于该井段属于垂直井段，体载项为零；地应力属于远场应力场，故在有限元计算时通过施加初始应力场来进行求解，由于该模型具有对称性，取其四分之一进行研究，建立了有限元力学模型。

图1采用映射网格技术来划分有限元计算单元，采用四边形四节点单元和高阶插值法来确定数值算法的稳定性，单元总数1632，节点总数1716。计算所需各项参数：井眼半径10cm，地层取10倍井眼尺寸进行研究，垂直地应力梯度0.023MPa／m，水平最大地应力梯度0.0253MPa／m，水平最小地应力梯度 0.0172MPa／m，初始孔隙压力 28.55MPa，弹性模量2.58×104MPa，泊松比0.182，Biot系数0.9，黏聚力9.72MPa，内摩擦角41.14°，孔隙度14%，热膨胀系数3.36×10－51／℃，初始含水率3%，饱和含水率10%，吸水扩散系数0.0243cm2／h，滤液密度1g／cm3，动力黏度3.1×10－4Pa·s，渗透率1.0×10－4mD，流体压缩率4×10－4MPa－1，岩石骨架压缩系数1×10－6MPa－1，基体密度2.6g／cm3，滤液热容4.2×103J／（kg·K），地层温度100℃，井壁温度110℃，计算水化膨胀应变时k1为0.0333、k2为0.832。

图1 有限元计算网格划分

应力边界条件：初始应力设置为地应力场，水平方向施加最大水平地应力，垂直方向上施加最小水平地应力，井筒施加等效钻井液液柱压力；模型左边界施加对称边界，模型右边界施加水平约束，模型上边界施加垂向约束，下边界施加对称边界。渗流边界条件：井筒施加钻井液液柱压差，左端和下端施加对称边界，其余设为零通量。初始条件设置：初始状态下，各应力和渗流初始条件均设置为井眼钻开前原始地层参数。

2.2 计算结果及分析

数值求解了钻井工况正压差为7MPa时，不同时间内含水量、孔隙压力及井周应力分布。图2、3分别为径向方向上含水率分布和孔隙压力分布的变化。

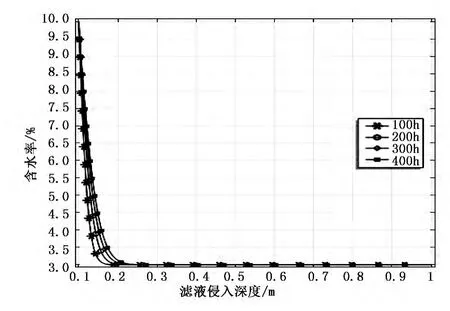
图2 井眼钻开后径向方向上含水量分布

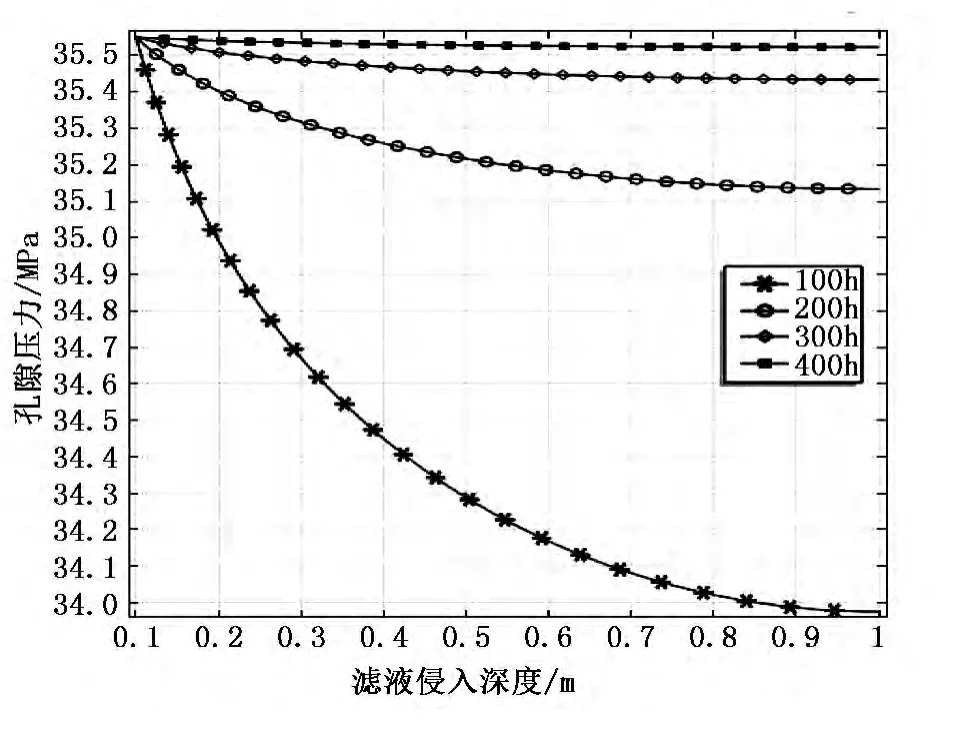
图3 井眼钻开后径向方向孔隙压力分布

当在钻遇泥页岩地层时，井眼径向方向上发生传质传能，由于泥页岩的渗透作用，主要有水力压差渗透及钻井液的封堵作用，使得封堵和压能传递及物质传递呈现出与时间的相关性，从而表现出井壁存在一个稳定周期。由图2分析出，当井眼初始钻开时，井壁周围的含水率首先达到饱和，随着井眼暴露在钻井液中，含水率曲线逐渐上升，但上升的幅度较低，滤液侵入深度为0.2m，是井壁失稳主要发生的区域；图3展示了孔隙压力传递，与图2相比，从曲线斜率可以判断，孔隙压力传递速度明显快于物质传递，在钻开200h以后，压力传递曲线就趋于平稳，当钻开300h以后地层孔隙压力几乎不变。因此，钻井施工设计钻井液的时候不但要考虑物质传递引起的水化作用，而且要考虑可能潜在的波动压力引起孔隙压力波动，故要提高钻井液的封堵作用，封堵因压力波动造成的突发性井壁失稳。

图4、5分别为井筒周围沿最小水平主应力方向和最大水平主应力方向的井周应力径向分布。

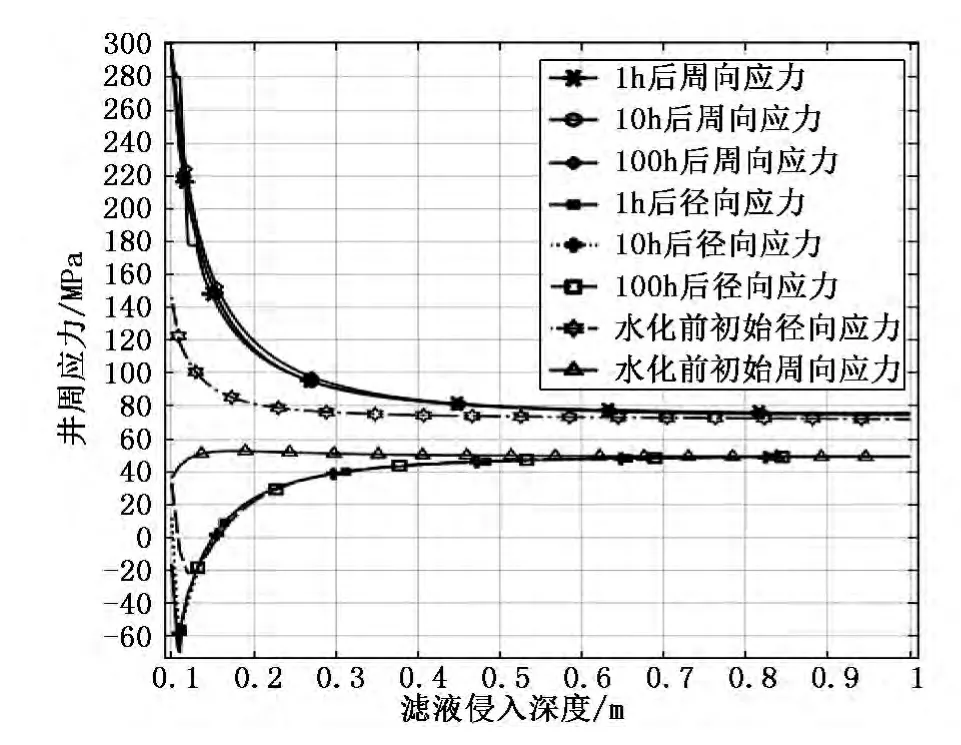
图4 沿最小水平主应力方向井周应力分布

图5 沿最大水平主应力方向井周应力分布

可以看出，水化前井周应力都为正值，即应力方向沿井筒方向，滤液侵入造成泥页岩水化膨胀，由于膨胀应力的存在，最终导致径向应力方向发生转变，即原来的井筒方向转变向地层方向，但随着径向距离增大，径向应力方向又指向井筒；其次还可以看出距井壁0.4m内，水化导致周向应力和径向应力都增大，且初始时增大的速度最大，随着水化时间的进行，应力增值逐渐减小，可能是因为黏土颗粒之间相互膨胀，黏土含水增加，膨胀力逐渐增大，进而导致颗粒与颗粒之间相互挤压，由于膨胀应力张量的存在，使得有效应力大小和方向也随之变化，且由于膨胀应变是含水率的函数，膨胀应力在空间质点上各向异性，所以导致井周应力的大小和方向都随着空间和时间变化。因此，在分析应力变化时，要考虑到膨胀应力的时空变化，从微观的角度建立各向异性的膨胀应力，除了考虑膨胀应力张量的正应力之外，还须考虑膨胀应力的剪应力部分。

利用D－P准则来判断岩石破坏，通过F函数的正负来判断井壁坍塌破坏的程度。当F＞0时，井壁无破坏，当F＜0时，井壁破坏；负值越大，坍塌破坏的程度越大，也可通过F的正负值确定塑性区的范围。图6为随着时间变化，井壁坍塌破坏程度。

图6 不同水化时间井壁破坏程度

由图6可以看出，水化初始，无膨胀应力及井壁岩石强度变化，钻井液能起到支撑井壁的作用，故井壁岩石没有发生压缩破坏，随着滤液侵入，即打开井眼后，钻井液形成泥饼，滤液逐渐侵入，岩石强度逐渐降低，泥页岩地层发生水敏性膨胀，膨胀压力发生，再由于温度的影响，化学场与应力、温度场的耦合作用，最终导致井周应力二次分布，并且分布呈现动态变化的过程，原因是膨胀应力张量的时空变化导致井周应力的大小和方向都在发生变化。膨胀1h后，井壁发生轻微的坍塌，主要原因是井壁首先见水，立即达到含水饱和度，水化膨胀，10h后，破坏区域已经延至15cm，该区域发生了塑性屈服，当达到100h后，坍塌已经非常严重，由原先的最小主应力方向发展至最大主应力方向，并且破坏区还进一步增大，此时用于钻井液的泥浆密度势必调整，以重新建立井壁应力平衡；或者立即采取完井措施，快速通过不稳定层，在最佳时间内完成固井。