基于集合覆盖模型的装备故障诊断方法研究＊

杨锡铅 李 赟 张洪华

（1．92730部队 三亚 572016）（2．91388部队 湛江 524022）

1 引言

随着武器装备的不断发展，其结构与组成越来越复杂，装备的复杂化在带来装备性能提高的同时也导致其故障概率大幅提高。故障诊断是装备技术保障的重要内容之一，故障的检测与诊断已经成为影响战备完好性、使用和保障费用的主要因素［1～2］。目前的故障诊断方法是对关键部件设计BIT 装置和进行状态监控［3～4］，当状态超出预置则给出故障报警提示。但该方法大多依靠人工经验判断是否为故障，缺乏故障推理机制，一般不能隔离故障。本文以故障测试相关性矩阵为基础，将故障诊断过程归纳为经典的集合覆盖问题，通过快速求解该数学问题，给出故障诊断结果，单故障和双故障实例证明该方法合理有效。

2 集合覆盖问题故障模型

2．1 故障建模

表1是某装备故障测试相关性矩阵［5］，其中系统故障为s1～s7，p（si）为其对应的先验概率，有t1～t9共九个测试点。根据Bayes概率理论［6］，故障诊断问题可以表述为：已知所有故障si∈S的先验概率p（si）和故障现象O（T），求具有最大后验概率的故障集合X，即

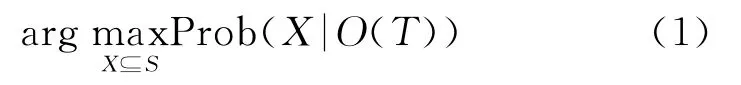
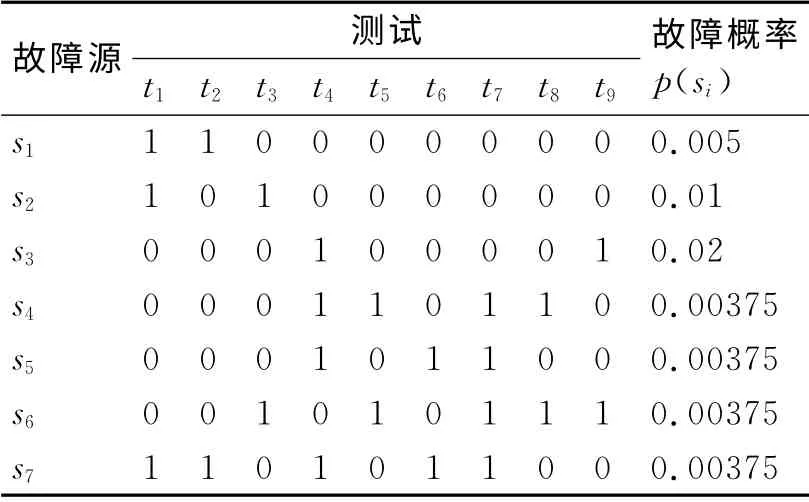
表1 某故障测试相关性矩阵

由Bayes公式

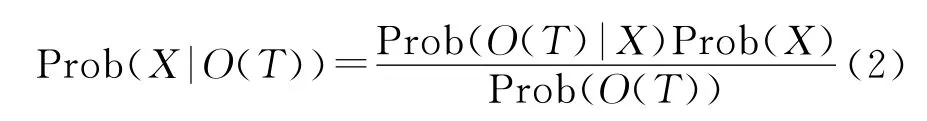
定义m维向量x＝［x1，…，xi，…，xm］，当xi＝1时有si∈X，xi＝0时si∉X。则有：

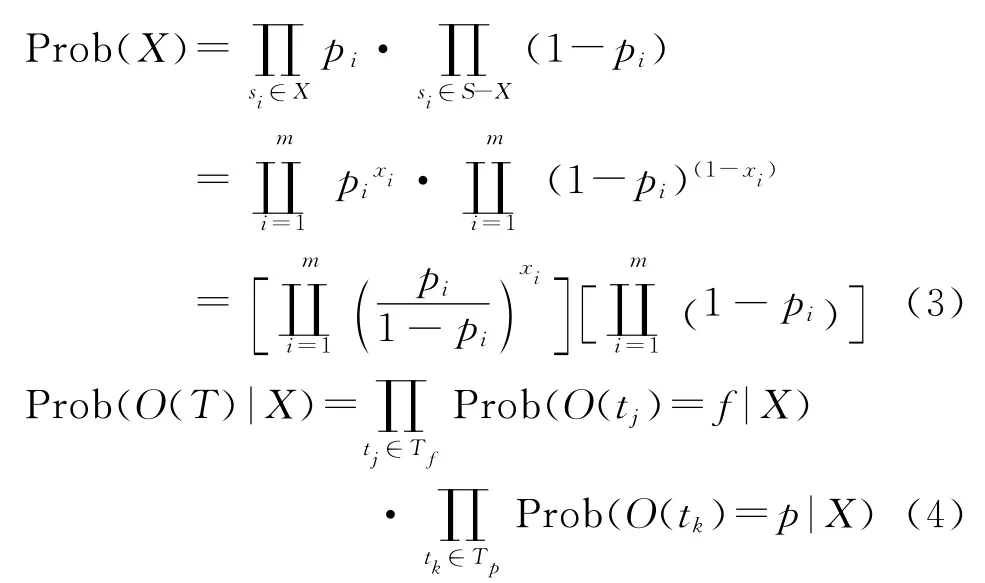
其中：

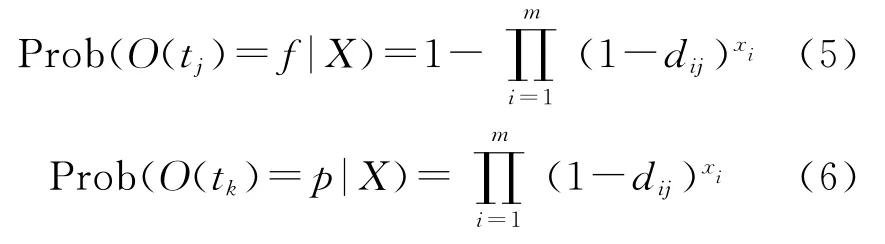
由此得到：

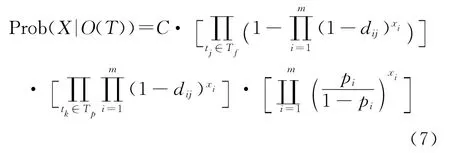
其中：

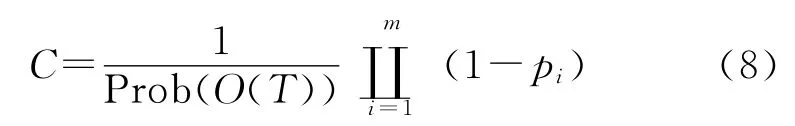
为常数。这里假定该系统故障测试为二值测试，每个测试的结果只有“通过”（dij＝0）、“不通过”（dij＝1）两种情况，分别用Tp和Tf表示。因此，该诊断问题可看作一个非线性组合优化问题，即在所有2｜S｜个故障集合中，求取一个故障集合X，使arg

2．2 集合覆盖问题推导

分析式（5）和式（6）发现，对于任意dij＝（0，1），Prob（O（tj）＝f｜X）与Prob（O（tk）＝p｜X）的值只能为1 或0，要使式（7）取得最大，即满足arg，必须在Prob（O（tj）＝f｜X）和均不为0的前提下，使取得最大值。可以证明，目标函数Prob（X｜O（T））取得最大值的必要条件是：

1）对于O（tj）＝f，必须至少有一个xi＝1使得dij＝1；

2）对于O（tj）＝p，当dij＝1时，必有xi＝0；

当Prob（O（tj）＝f｜X）＝Prob（O（tk）＝p｜X）＝1时，式（7）所示的目标函数Prob（X｜O（T））可以改写为

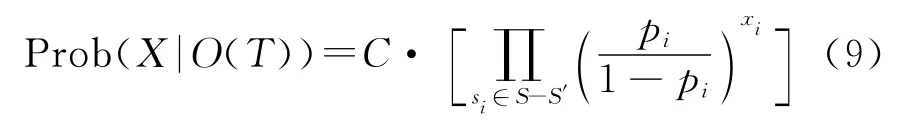
其中为C常数。两边同时取负自然对数：

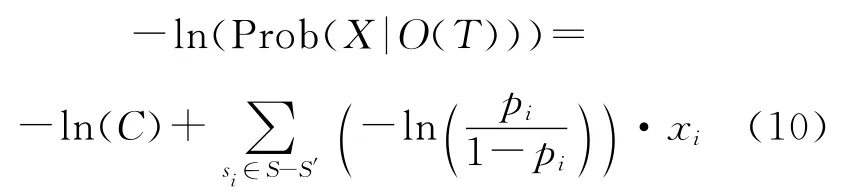
由此，式（1）所示的诊断问题可以表示为

式中ci＝-ln（pi／（1-pi）），D′＝（D-）T。

由此，我们将该故障诊断问题转化为了集合覆盖模型的求解。

3 求解集合覆盖问题

集合覆盖问题已被证明是NP 完全问题。求解方法主要有两类，一是完整算法［7～9］（exact algorithms），这些方法计算量大，耗时长。为了解决这一问题，许多学者转到第二类启发式算法（heuristic algorithms）的研究上，使得能够在可以接受的时间内求得问题的近似最优解，如贪婪算法、基因算法、拉格朗日松弛算法、神经网络算法等［10～13］，取得了不错的效果。本文选用拉格朗日松弛经典算法，具体求解过程可见文献［12］。

由于多故障诊断情况非常复杂，一般难以通过BIT 获得准确的诊断结果，这里假设系统最多只会出现两个故障同时发生的情况。

对于表1所示的系统故障源s1和s2双故障并发，此时系统报警测试集｛t1，t2，t3｝，操作员根据测试性设计图纸（即测试相关矩阵），会认为系统的潜在测试故障集为｛s1，s2，s3，s4，s6｝（测试1，2，3列中数值1对应的行），需要通过其它手段进一步排查，才能获取更准确的诊断结果。按照本文的方法，诊断系统能够在短时间内给出的诊断结果｛s1，s2｝。

单故障诊断结果见表2，按本文算法得到的诊断结果，计算出故障检测率rFD＝100%，故障隔离率rFI＝100%。

双故障诊断结果见表3，本文算法得到的诊断结果，其故障检测率rFD＝100%，故障隔离率rFI＝80．95%，诊断时间非常短。

表2 单故障诊断结果

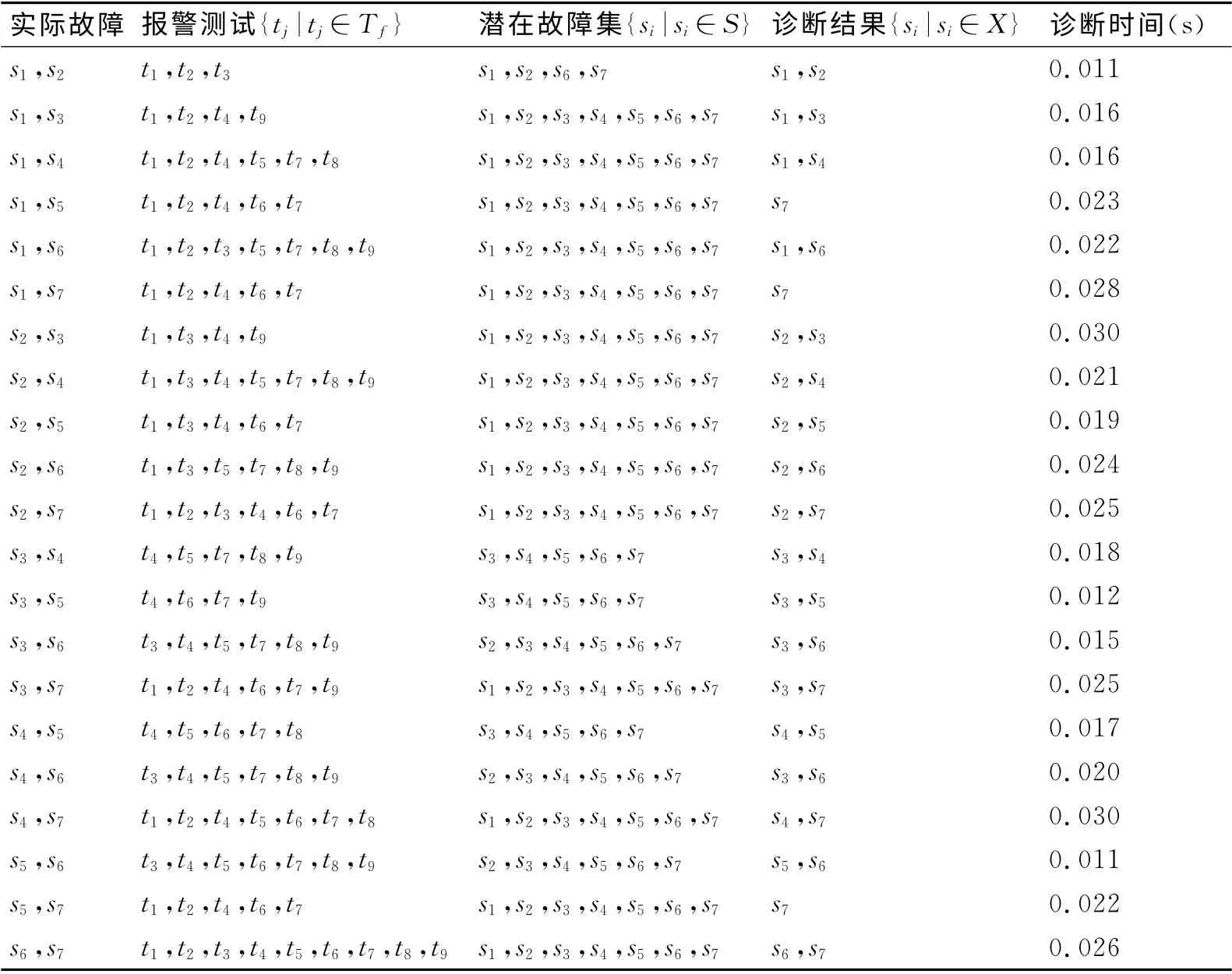
表3 双故障诊断结果

4 结语

本文针对机内测试功能单一，不能给诊断结果的问题，提出一种基于集合覆盖模型的故障诊断方法。首先利用Bayes概率理论对机内测试的结果，即故障测试相关矩阵进行分析建模，然后将该故障模型转化为集合覆盖，最后解算该模型。实例分析证明，该方法对单故障和双故障诊断能得到满意的结果。

［1］曾天翔，张宝珍．军用飞机维修面临的挑战与发展前景［J］．航空维修与工程，2005（1）：28-31．

［2］Teal C，Larsen W．Training key to electrical systems maintenance［C］／／Proeeedings of the 21st Digital Avionics Systems Conference，2002（2）：1-9．

［3］曾天翔．电子设备测试性及诊断技术［M］．北京：航空工业出版社，1996．

［4］Dress R，Young N．Role of BIT in support system maintenance and availability［J］．Aerospace and Electronic Systems Magazine，2004，19（8）：3-7．

［5］李赟，蔡志明．大型复杂系统测试序列优化［J］．计算机集成制造系统，2010，16（9）：1961-1966．

［6］Shakeri M，Pattipati K，Raghavan V．Optimal and near-optimal algorithms for multiple fault diagnosis with unreliable tests［J］．IEEE Trans on systems，Man and Cybernetics，1998，28（3）：431-440．

［7］Fisher M，Kedia P．Optimal solution of set covering／partitioning problems using dual heuristics［J］．Management Science，1990，36：674-688．

［8］Beasley J E，Jansten K．Enhancing an algorithm for set covering problems［J］．European Journal of Operational Research，1992，58：293-300．

［9］Balas E，Carrera M．A dynamic subgradient based branch-and-bound procedure for set covering［J］．Operations Research，1996，44：875-890．

［10］Haouari M，Chaouachi J S．A probabilistic greedy search algorithm for combinatorial optimization with application to the set covering problem［J］．Journal of the Operational Research Society，2002，53：792-799．

［11］Aickelin U．An indirect genetic algorithm for set covering problems［J］．Journal of the Operational Research Society，2002，53：1118-1126．

［12］Beasley J E．A Lagrangean heuristic for set covering problems［J］．Naval Research Logistics，1990，37（1）：151-64．

［13］Ohlsson M，Peterson C．An efficient mean field approach to the set covering problem［J］．European Journal of Operational Research，2001，133：583-595．