基于越级指挥方式的指挥网络稳定性分析＊

彭义波 邢焕革

（1．海军工程大学 武汉 430033）（2．海军92961部队 三亚 572021）

1 引言

信息化条件下的现代战争，共享信息程度高，传输方式多样化、速度快，对指挥体系的高效、稳定运行提出了极高的要求。在紧急情况下或执行特殊任务时采取越级指挥，在一定程度上可以提高指挥效率，但也打破了正常的指挥网络体系结构，因此对越级指挥方式下指挥网络拓扑结构进行分析，研究越级指挥方式下网络的结构变化对稳定性的影响，对于提高指挥网络稳定性有着重要意义。目前针对指挥网络稳定性问题国内外学者进行了深入的研究，如秦伟等使用熵理论分析了作战指挥网络的稳定性［1］，朱涛等提出了基于节点收缩改进方法的指控中心性评估模型，寻找指控中心节点从而进行针对性防护［2］；Albert分别研究了随机网络和BA 网络在随机攻击和选择性攻击策略下的抗毁性［3］，Callaway等研究了在渗透和随机图中网络的鲁棒 性 和 脆 弱 性［4］，Hyoungshick Kim、Ross Anderson研究了动态网络问题，得出网络的连通性依赖于少数高度活跃的节点和边［5］，但针对越级指挥条件下的网络稳定性研究较少，本文将在已有研究成果的基础上，着重就越级指挥方式下指挥网络稳定性进行研究。

2 越级指挥网络拓扑结构

在作战中通常情况下采用逐级指挥方式，但在紧急情况下或执行特殊任务情况下，为了不延误战机，有时也会采取越级指挥方式，特别是在现代化战争中，越级指挥方式将会经常使用。

2．1 逐级指挥网络的拓扑结构

逐级指挥通常是按照指挥关系和指挥权限逐级进行的指挥，在结构上，各级指挥机构在纵向上根据隶属关系构成了层次结构［6］，在横向上根据指导与协同关系形成了平行结构。从总体上看，逐级指挥关系是一种树状结构，为此，运用网络理论对指挥体系拓扑化，将指挥机构抽象为网络中的节点，指挥关系抽象为边。根据文献［7～8］，可以得到指挥层次L＝4，跨度S＝3的指挥网络拓如图1所示。

图1 L＝4，S＝3指挥网络拓扑图

图2 三次越级后指挥网络拓扑图

2．2 越级指挥网络拓扑结构

越级指挥是指在紧急情况下或执行特殊任务的部队，超越一级或数级实施的一种指挥方式［9］。对于作战指挥网络而言，即在一定条件下，上级节点越过K（K＞1）层与下级节点直接建立连边关系，同时断开该下级节点与原直接相连的上级节点之间的连边。在2．1逐级指挥网络的基础上，越级指挥网络的具体的生成方法如下：

1）假设需要对节点P实施越级指挥，越级层次为k（0＜k＜L-1），节点P的上级节点为U，实施越级指挥节点为T。

2）对一个节点实施越级指挥时，节点T与节点P直接建立连边关系，节点P与其上级节点U之间的连接关系断开，即节点P与节点T之间建立了新的连边关系。

3）当对多个节点实施越级指挥时，按照2）的方法依次完成所有节点的越级过程，生成新的指挥体系的网络拓扑结构，图2是在图1所示网络的基础上3个节点实施越级指挥后的网络拓扑结构图。

对照图1～2可以看出，越级指挥方式下指挥网络的结构改变很大，必然也会导致网络稳定性发生改变。

3 模型的构建

越级指挥作为紧急情况下或执行特殊任务情况下的一种指挥方式，对作战任务的完成具有举足轻重的作用，但越级指挥也打破了常规指挥关系，使正常的逐级指挥关系出现重组，在这种情况下，整个指挥体系的稳定性将会受到影响。对于这种影响，本文从两个方面展开研究：一是静态条件下越级指挥网络结构稳定度，即没有受到攻击时，通过指挥网络的结构拓扑特征体现网络的结构稳定度；二是越级条件指挥网络的动态稳定性，即受到攻击（随机和选择）的情况时，通过计算比较网络最大连通子图来分析研究指挥网络的稳定性。

3．1 结构稳定度模型

指挥网络具有多层级、多功能的结构，网络结构的好坏直接决定了指挥网络的性能，影响着指挥网络的稳定性。在越级指挥方式下，指挥网络的拓扑结构发生改变，因此本文在研究指挥网络中指挥节点在越级指挥方式下度的分布变化基础上，提出网络结构稳定度的概念，用以衡量指挥网络的结构变化情况，其模型如下：

式中k（i）代表网络中每个节点的度；表示整个网络的平均度；A表示整个网络节点之和A＝

显然，当网络为全连通网络时，G＝1此时网络最稳定；当网络中节点度分布越不均匀G值越小，即此时网络的结构稳定度越差。

3．2 网络指挥效率模型

对于指挥网络来说，网络的平均路径长度表示信息在网络中的传输时间。网络效率用来衡量网络中指挥节点与指挥节点之间的信息流通快慢程度，通常定义为与网络最短路径长度成反比［10］：

式中dij代表节点i和节点j之间的最短路径，在指挥网络中表示为节点i、j之间的链路数。

3．3 指挥网络动态稳定性模型

指挥网络动态稳定性是指受到攻击的情况下，指挥网络继续保持一定指挥功能的能力，攻击行为通常分为随机攻击和选择性攻击两种模式。本文运用网络最大连通子图和最大连通率［11］的方法，在不考虑信息负载，设定攻击成功概率为1的情况下，分析指挥网络在越级指挥方式下节点受到攻击后最大连通子图来评价网络的稳定性。

3．3．1 指挥网络稳定性模型

假设指挥网络的初始时有N个节点，在越级指挥方式下受到攻击时有若干个指挥节点失去功能，与之相连的指挥节点之间的连边断开，此时指挥网络分解为若干个指挥子网络，分别计算每个子网络所包含的指挥节点数，得出最大的连通子图所包含的指挥节点数目为n，定义MC为指挥网络的最大连通率，则指挥网络的稳定性模型为

式中MC为网络最大连通率；n表示最大连通子图中节点数目；N表示原网络节点数目。

3．3．2 随机攻击下的越级指挥网络稳定性分析模型

随机性攻击是一方不了解另一方的组织结构信息和单个节点在网络中的重要性的情况下，只是随机地选择另一方的指挥节点进行打击，攻击行为不具有针对性。下面是作战指挥网络在越级条件下以节点度为依据进行随机性攻击模型流程如图3所示。

3．3．3 选择性攻击下的越级指挥网络稳定性分析模型

选择性攻击是在掌握充分的情报信息的情况下，即一方已完全掌握了另一方指挥机构的信息，依据需要进行有选择性地打击对方重要目标的行为。在指挥网络中，通常以节点度（介数）来评估节点的重要性，下面是作战指挥网络在越级条件下以节点度为依据进行选择性攻击模型流程如图4所示。

图3 随机攻击流程图

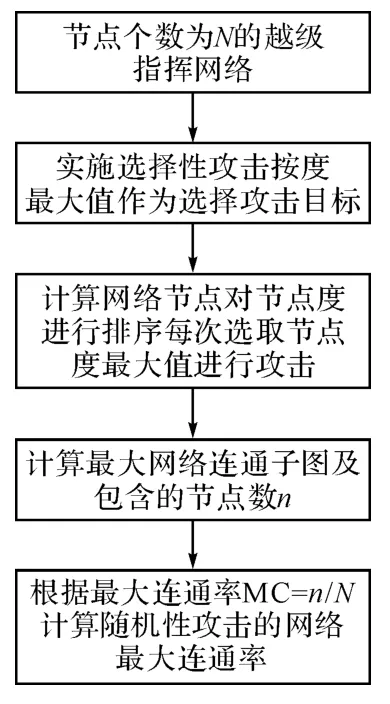
图4 选择攻击流程图

4 仿真计算与分析

假设指挥网络的指挥层级L＝5、指挥跨度S＝3，节点个数N＝121时，按照越级指挥方式生成指挥网络，根据指挥网络的结构稳定度和网络效率模型，分别计算出在越级指挥网络的结构稳定度和网络效率；根据指挥网络动态稳定性模型仿真计算越级指挥方式下随机攻击和选择攻击下的网络最大连通子图及对应的最大连通率MC并以此衡量网络动态稳定性的大小。

4．1 指挥网络的结构稳定度和网络效率

根据前面假设，为简化计算，本文只考虑从第1层节点实施越级，当指挥层级L＝5时，在越级指挥方式下指挥网络可以实施越级指挥的越级层数K＝1、2、3，对应指挥网络中实施越级指挥的指挥层级为网络中的第3、4、5层，可以实施越级指挥的最大节点个数分别为9、27、81个，通过仿真计算，对应的结构稳定度和网络效率如表1～表3、图5所示。

图5 K＝1、2、3时网络的结构稳定度和效率

从图5和表1可以看出，同一指挥网络在相同的越级层次条件下对应不同的越级节点个数时，指挥网络的结构稳定度是随着越级节点数增加而递减，并且递减变化的幅度随着越级节点数的增加而增大；相对应的，网络指挥效率随着越级节点数增加而增大，随着越级节点数的增加，网络指挥效率变化幅度明显增大。通过对比指挥网络的结构稳定度和网络指挥效率，可以看出在越级指挥方式下，网络指挥效率得到提高，而网络的结构稳定度变差。

4．2 越级指挥条件下随机性攻击网络最大连通率

根据越级指挥方式下随机性攻击的网络稳定性计算模型，运用计算机仿真方法，计算指挥网络在不同越级层级和不同越级节点个数的情况下，受到随机性攻击后的网络最大连通子图和最大连通率。设指挥层级L＝5、指挥跨度S＝3，分别计算越级层级K＝1、2、3时，受到随机性攻击条件下的网络最大连通率如表2～表4所示。

表1 结构稳定度和网络效率

表2 K＝1时随机性攻击条件下指挥网络最大连通率

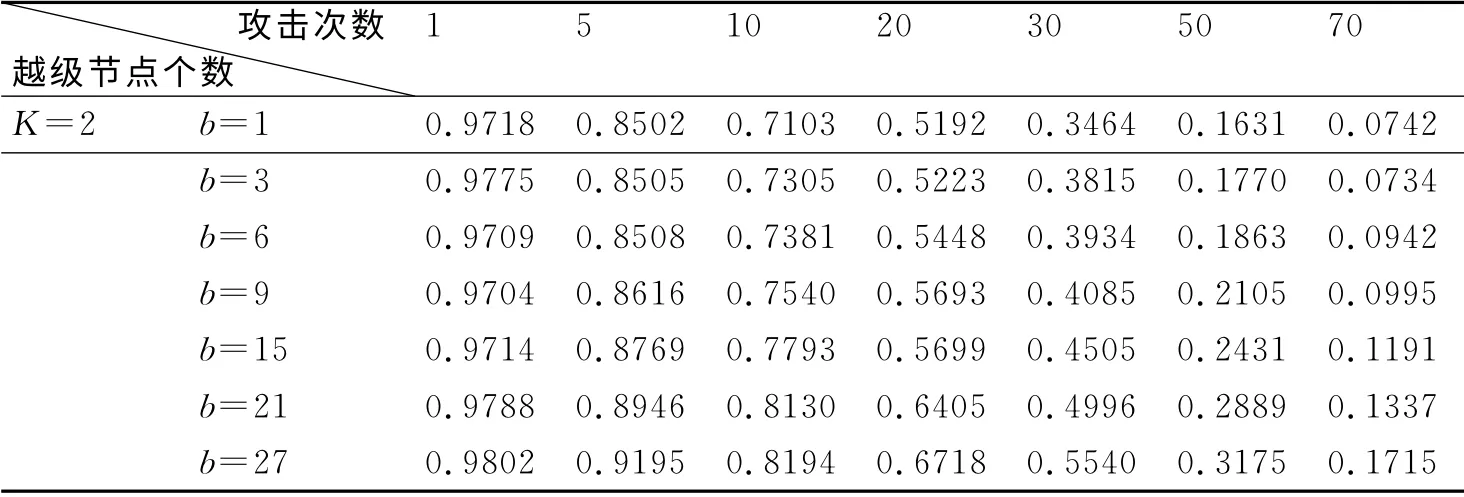
表3 K＝2时随机性攻击条件下指挥网络最大连通率

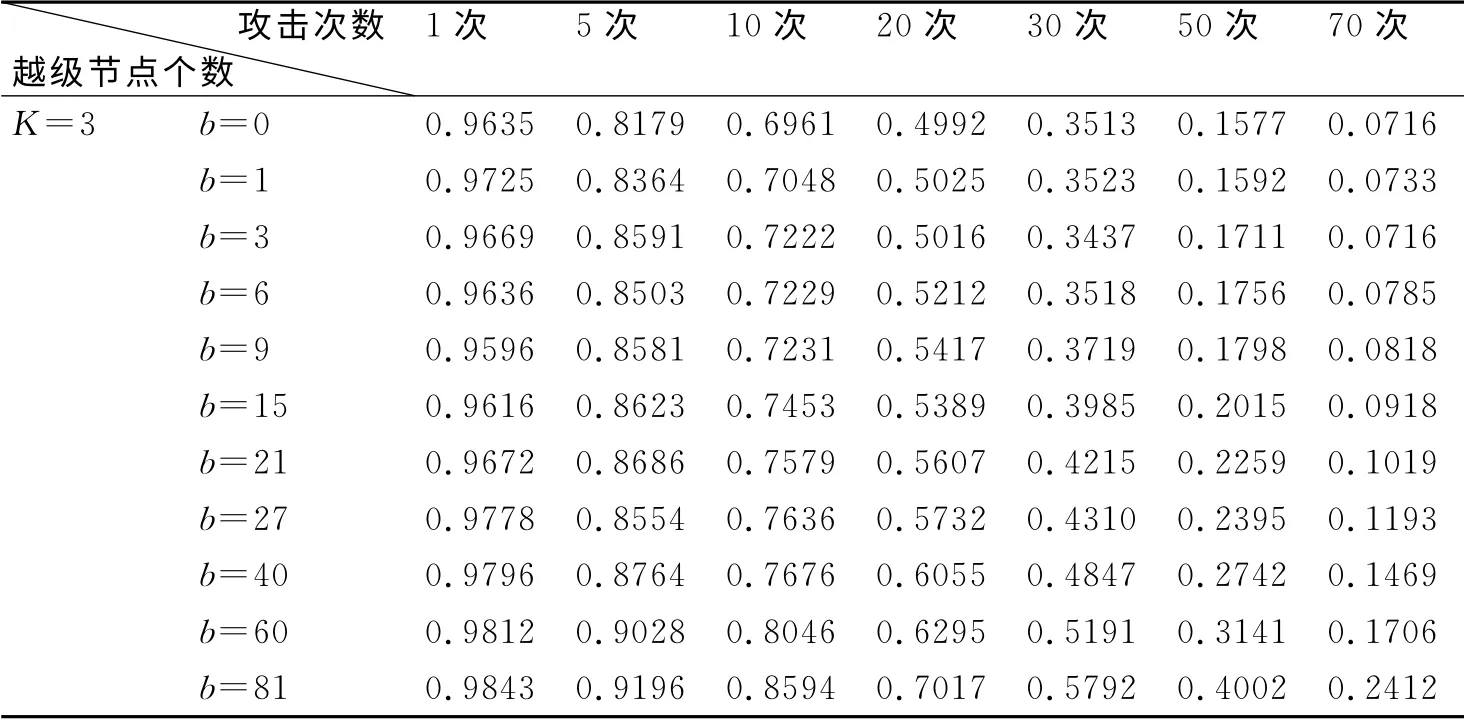
表4 K＝3时随机性攻击条件下指挥网络最大连通率

从表1～表4和图5可知，当越级指挥节点个数较少时，指挥网络的结构稳定度与网络指挥效率变化不大，当受到随机攻击时，指挥网络的最大连通率增加幅度很小，对应的变化曲线如图6所示。这是因为越级指挥节点个数较少时，采取越级指挥方式时，只是小幅度地提高了网络指挥效率，如表1所示。当越级指挥节点个数较多时，如表3和图5、图7所示，在越级层数K＝2时，指挥网络的结构稳定度随着越级节点个数增加表现为加速降低，网络指挥效率和最大连通率则加速增大。这说明指挥网络的结构稳定度在实施越级指挥条件下对于随机攻击是敏感的，网络最大连通率与实施越级节点个数、网络指挥效率有正向关系。综上所述，在随机攻击模式下实施越级指挥，网络指挥效率和稳定性得到提高，这与Wang［12］等研究结果相一致，即在越级指挥方式下，指挥网络在随机攻击模式下的稳定性要好于正常的逐级指挥模式。

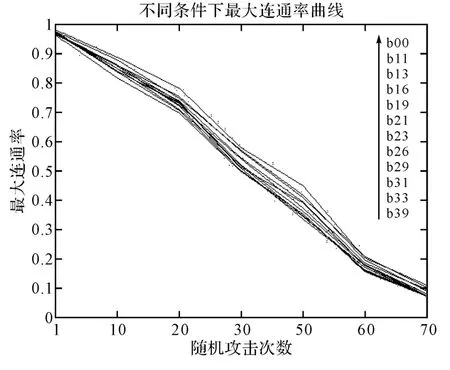
图6 越级节点个数为1～9时最大连通率曲线

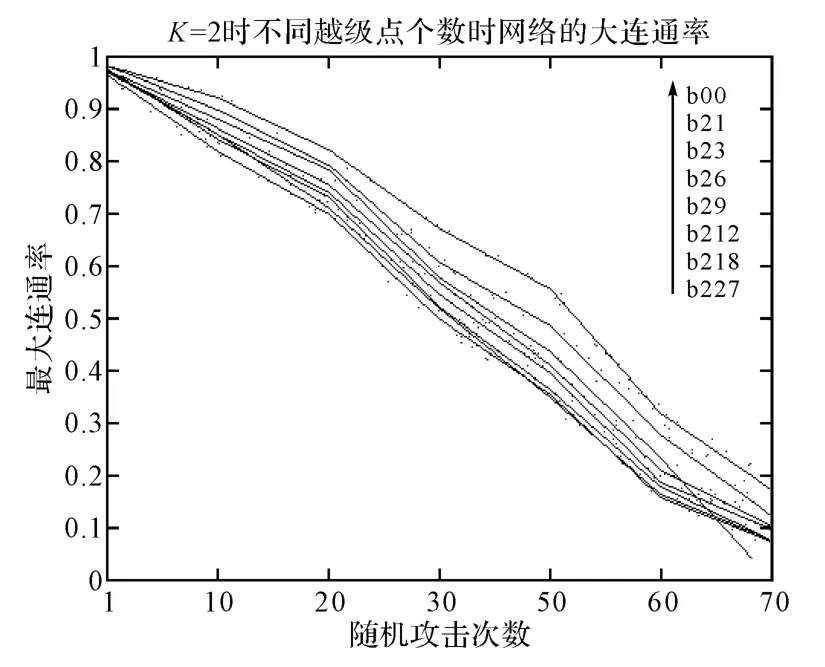
图7 K＝2时，最大连通率曲线

4．3 越级指挥条件下选择性攻击网络最大连通率

根据越级指挥方式下选择攻击的网络稳定性模型，运用计算机仿真方法，计算指挥网络在不同越级层数和不同越级节点个数的情况下，受到选择性攻击后的网络最大连通子图和最大连通率。在指挥层次L＝5、指挥跨度S＝3的条件下，分别计算越级层数K＝1、2、3时选择性攻击条件下网络的最大连通率如图8所示。

图8 K＝1、2、3时网络最大连通率曲线

表5 K＝2时不同越级节点个数最大连通率

从图8和表5可以看出，在越级层数相同的条件下，不同的越级节点个数对于选择性攻击具有很大的影响，总趋势是实施越级的节点越多，最大连通率下降越快，此结论刚好与随机攻击条件下相反。当越级层数相同时，对应于不同的越级节点个数，计算其分别对应相同的选择性攻击次数情况的最大连通率，结果如图9所示。

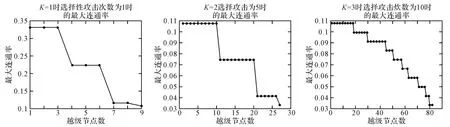
图9 相同越级层数K，不同越级节点数的最大连通率曲线

图9是越级层数K相同，越级节点数不同的情况下，对应于K＝1、2、3时分别取选择性攻击次数为1、5、10次所对应的最大连通率。从图9中可以看出，随着越级节点个数的增加，对于选择性攻击条件下的网络最大连通率变化幅度较大。结合图5、8、9 可知，对于选择性攻击条件下的指挥网络，其稳定性极其脆弱，且最大连通率与越级节点数目有反向关系。这是因为越级指挥方式提高了网络节点的集中度，网络组织结构稳定度降低，当面对选择性攻击时，网络中关键节点被攻击后造成的影响大于没有实施越级指挥的情况，因此面对选择性攻击时，越级指挥方式的稳定性小于逐级指挥方式。

5 结语

本文研究了越级指挥方式下的网络结构稳定度问题，分析计算了采用越级指挥方式时，指挥网络在静态条件下的结构稳定度和网络指挥效率。运用网络最大连通子图模型，分别仿真计算了指挥网络在随机和选择攻击情况下的网络最大连通子图和最大连通率。通过分析发现，指挥网络的结构稳定度和网络效率在越级指挥方式下具有反向关系，即越级指挥在提高网络指挥效率的同时，降低了网络的结构稳定度，对于随机性攻击而言，越级指挥方式比正常指挥方式具有更高的稳定性；同时，由于越级指挥方式改变了网络的结构稳定度，对选择性攻击更加敏感，网络的稳定性更差。

［1］秦伟，屈洋．作战指挥系统稳定性分析［J］．指挥控制与仿真，2008，30（2）：14-16．

［2］朱涛，常国岑，郭戎潇，等．网络化指挥控制中心性建模评估研究［J］．系统仿真学报，2010，27（11）：4084-4086．

［3］Reka Albert，Hawoong，Barabasi AL．Error and attack tolerance［J］．Nature，2000，406：378～382．

［4］Callaway，Newman，Strogatz AL．Network robustness and ragility：Percolation on random graphs［J］．Physical Review Letters，2000，85：5468-5471．

［5］Hyoungshick Kim，Ross Anderson AL．Temporal node centrality in complex network［J］．Physical Review，2．12，E85：026107（1-5）．

［6］俞杰，王伟，张国宁．基于复杂网络的联合作战指挥体系研究［J］．火力指挥与控制，2011，36（2）：5-10．

［7］杨立峰，代进进，李相民．舰艇编队网络化反导作战指挥体系研究［J］．海军航空工程学院学报，2011，26（4）：457-461．

［8］权良涛．基于复杂网络理论的作战体系网络建模研究［D］．西安：西安电子科技大学，2012：35-37．

［9］秦进，史峰，邓连波，等．道路交通网络效率定量评价方法及其应用［J］．吉林大学学报（工学版），2010，40（1）：47-51．

［10］2011年军语．

［11］董尧华．城市复杂交通网络系统脆性管理研究—以青岛为例［D］．青岛：中国海洋大学，2011：29-34．

［12］WANG Bing，TANG Huanwen，GUO Chonghui，et al．Optimizagion of network structure to random failures［J］．Physica A：Statistical Mechanics and its Applications，2006，368（2）：607-614．