负压泵工作状况下泵膜片力学性能研究
2014-11-22杨胜林张露杨涛赵三星
杨胜林,张露,杨涛,赵三星
(1.林泉航天电机有限公司,贵阳 550008;2.中铁五局集团建筑公司,贵阳 550002;3.武汉科技大学,武汉 430081)
0 引言
在航天航空领域、宇航领域,绝大部分产品都处于低于标准大气压下的环境中工作,为了深入研究上天后产品的状况,需要在研制产品时充分地验证和做实验对其摸底工作,分析产品的测试记录是否达到各项技术指标要求。在该情况下需要提供相适应的工作环境。还有一些深水中工作的产品需要增大其外部压力才能模拟分析真实过程。因此,将一定空间内的环境气压降低到预定值需要特定的装置来实现。
改变一定空间内气压有很多种方式,比较直观的有容积改变、恒定内腔气体的抽出或充注。在容积恒定的情况下,通过真空泵能很好地实现对密闭恒定容器内的气体进行抽出或充注。常见的真空泵结构形式有往复膜片式、齿轮泵、柱塞式、离心式等几种。其中往复膜片式真空泵具有结构简单、可靠性高及结构紧凑的特点,因此通过往复式膜片泵来实现预定环境的应用比较普遍,所以本文以研究往复式膜片泵工作时的力学特性作为重点关注对象。
1 真空泵工作原理及几何模型
对于往复式膜片泵,其组成包括驱动电机、泵体、进出口管道、密闭容器等,几何结构如图1 所示。其工作原理为电机提供驱动力,使与电机输出端相连的回转偏心轴绕电机轴线转动,回转偏心轴上与轴承配合的小圆柱体存在一定的偏心量。因此,轴承将以电机回转轴线为中心,以偏心轴小端偏心量为半径做圆周运动。轴承的圆周运动使得与之配合的连杆顶端也做圆周运动。由于泵膜片上端面被紧固在连杆上,泵膜片随着电机的旋转周期性地上下左右的摆动,实现泵膜片与底板围成的空间体积变化。而单向阀的作用是保证工作时不会出现气体从另一个气口溢出或吸入的情况,而保证泵的效率。
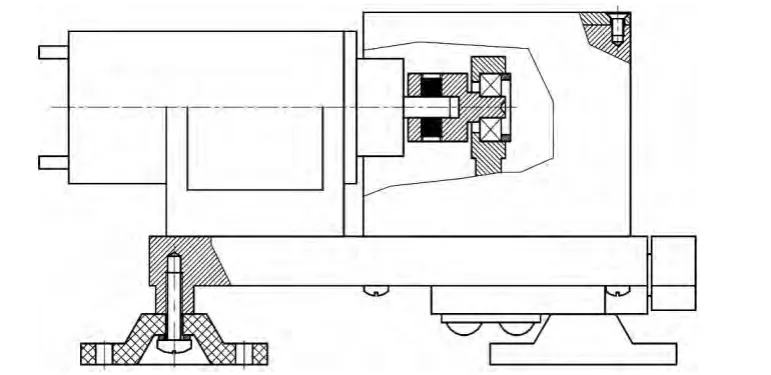
图1 往复式膜片泵整体结构
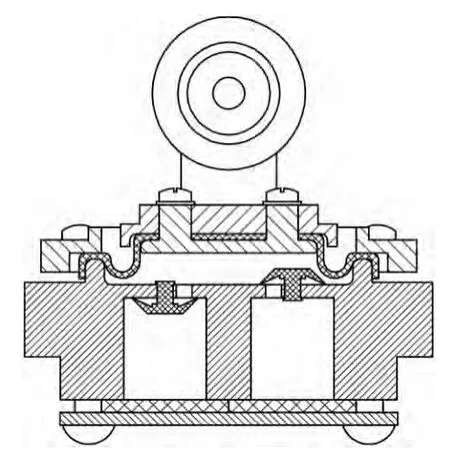
图2 泵体组成部分结构图
泵体包含了连杆、泵膜片、泵膜片挡板、泵膜片压板、阀膜片等,这是泵工作时最关键的部分,也是生产加工时的关键件和重要件,其加工精度直接影响到泵体的密封性与效率,同时还是影响流量和真空度或容器压强大小的关键参数。其结构如图2 所示。
2 负压泵工作时相应数学模型
2.1 泵容器压强计算数学模型
假定初始状态时进出气口和泵膜片空腔处于标准大气压P0下,且连杆上轴承的轴线与电机回转线重合。设泵膜片与底板所围成的空间为V1,进气口相连的容器容积为V2,假定泵膜片的等效横截面为s,偏心轴的小端圆柱的偏心量为h。
根据气体的特性,压强与密度成正比关系,质量一定时,压强与体积的乘积恒定。在从进气口抽气开始到结束的过程中,泵膜片所在空腔内与抽气口空腔内气体的总质量恒定,按照质量守恒定律,计算出第一次抽气后的容器V2、压强P1如下式:(V1+V2+hs)×P1=(V1+V2)×P0。
第二次抽气时,V2空腔内初始压强为P1。同理,按照质量不变原则,第二次抽气后的压强按下式计算:
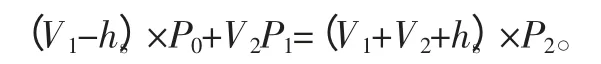
第三次抽气时:(V1-hs)×P0+V2P2=(V1+V2+hs)×P3。
第四次抽气时:(V1-hs)×P0+V2P3=(V1+V2+hs)×P4。
以此类推,第N 次抽气后进气口的压强迭代公式如下:
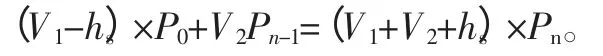
2.2 泵真空度数学模型
真空度的计算可以通过两种方式进行,一种是按照进气口两端压强差;另一种是按照给泵膜片提供的驱动来计算真空度。
(1)抽气口的真空度取决于泵膜片体积空间的压强,在泵膜片空间抽气过程中,若该空间体积最大时的压强等于V2内压强时,停止抽气,该状态下即达到真空值。
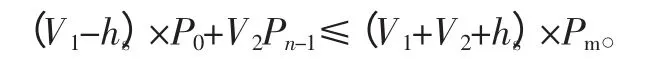
(2)根据给泵膜片提供动力的电机来计算,根据结构特点,泵膜片的运动是通过膜片挡板来传递的,而膜片挡板的运动是通过连杆绕心轴回转实现,所以泵膜片运动由膜片挡板驱动。整个膜片挡板和连杆的运动则由电机提供,很显然,根据力学原理有:

式中,S*为泵膜片当量横截面面积,Pm为达到真空度时变动空间的压强,h为偏心量,M为电机输出轴承受的负载,K为与摩擦、密封性阻尼等相关的系数,η为传递效率。
考虑到在V2内达到真空值时,V2+hs空间内的压强和V2内一致,否则V2还没有达到稳定的真空度值。因此上式Pm就是真空度值,体现了电机承载能力与真空度之间的关系。
从上两种分析真空度值来看,第一种分析方式计算麻烦。即必须要把每一次V2内压强计算出来与V1+hs内的压强做一个比较。这不仅会增加很多的工作量,而且还存在计算误差问题,通过多级迭代后误差会被放大,很可能严重影响到结果的准确性。采用第二种方式计算比较可靠,只需要准确计量膜片挡板的面积与芯轴的偏心量。
本产品的泵膜片在实际工作过程中由于存在弹性和塑性的变形,以至于其当量横截面面积无法计算,因此只能通过试验得到其真空度的值。通过对该产品试验考核,得到本批次产品在当前工况下的真空度满足用户指定的指标30kPa。后续仿真计算所使用的真空度都是用该试验值进行。
2.3 泵力学本构方程模型
由于泵体除阀膜片和泵膜片外都是各向同性材料,泵膜片和阀膜片属超弹塑性材料,因而属于瞬态动力学计算范畴。由弹塑性力学有限元法,分析在笛卡尔坐标系下的力学平衡方程:
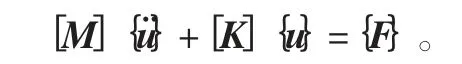
式中,[M]为系统质量矩阵,[K]为系统刚度矩阵,{u¨}为各节点加速度向量,{u}为各节点位移向量,F为载荷向量。
由于该负压泵的材料除泵膜片外皆为弹塑性各向同性,它的本构方程在线弹性条件满足下叠加原理,在弹性区内应用经典弹性理论的广义Hooke 定律有[1]:
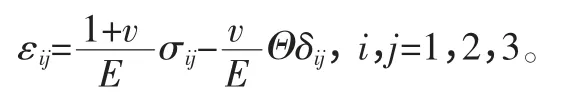
式中,E为材料的杨氏模量,v为材料的泊松比,Θ为体应力Θ=σx+σy+σz。
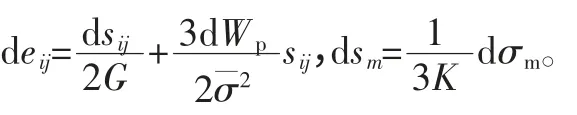
3 负压泵物理模型及计算结果
根据上述分析的工作原理,电机给偏心轴A 提供旋转速度与一定的力矩,本文关心的是泵膜片在工作时的承载情况,因此只需将电机的输出转速和负载作为负压泵与电机接口处偏心轴的输入即可,要分析的模型如图3所示。泵体工作时体积变化关键在泵膜片(红色)的形状改变,泵膜片的A、B 平面被泵膜片压板D 和底板B 固定,C、D 平面固定在泵膜片挡板与连杆E 上,随着连杆的运动而运动,进而实现泵膜片和底板之间空腔的体积变化。其几何尺寸如图3 所示。
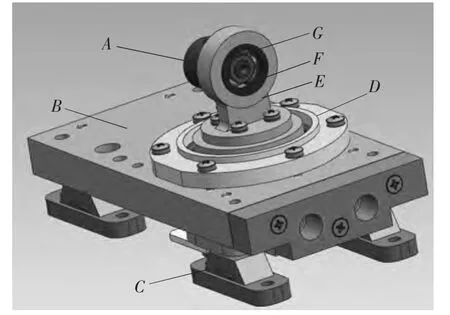
图3 负压泵物理模型(不含电机)
按照上述分析,在有限元计算强度过程中需将轴承G内部建立动摩擦接触对,对通过紧固件连接的地方设置为绑定接触,以简化过程和降低计算时间。对轴承和连杆的轴承室接触处,由于其处间隙配合公差不到一道,故可以简化计算成绑定接触。对减震垫施加全约束,偏心轴施加电机的输出转速,然后计算出该状态下的泵膜片应力与位移的分布情况。

图4 泵膜片几何尺寸
根据实际工作情况,对泵膜片单独分析,对泵膜片的A、B、D 共3 个面及4 个圆孔内表面进行固定,计算其前6阶振型,如图5~图10 所示。
经试验验证,该泵膜片的前6阶振型与如上仿真振型趋势是一致的,因此模态仿真结果是可信的。

图5 泵膜片1阶振型

图6 泵膜片2阶振型

图7 泵膜片3阶振型

图8 泵膜片4阶振型

图9 泵膜片5阶振型

图10 泵膜片6阶振型
当前状况下,初始位置时泵膜片不受到内腔和表面所处的气压差,电机输出端的偏心轴偏心量为3 mm,经Workbench 仿真计算,得到泵膜片在不考虑腔体内真空度的影响时,该膜片的位移大小分布和应力分布分别如图11 与图12 所示。
在不考虑真空度影响条件下,泵膜片的最大位移为3.009 6 mm,泵与偏心量3.0 mm,因此,从位移角度来分析,变形是合理的,泵膜片的位移比偏心量略大一些(0.01 mm),这是由于泵膜片在拉伸压缩后会产生微小的挤压变形且存在一个离心作用,使得泵膜片的位移量略大于偏心量。膜片运动到垂向最大位置时应力分布极值为30.2 kPa,处于泵膜片与膜片底板凸台结合处。而泵膜片材质为氟橡胶,其用于压缩空气的橡胶材料能承载不小于60 MPa 的工作压力,因此,当前工况下膜片承载能力能满足使用。

图11 泵膜片在不考虑真空度下的位移云图

图12 泵膜片在不考虑真空度下的应力云图
当偏心量为0.84 mm,且考虑泵膜片与底板所围腔体内存在一定真空度(30 kPa)的影响时,该膜片的变形程度分布和应力分布分别如图13 与图14 所示。
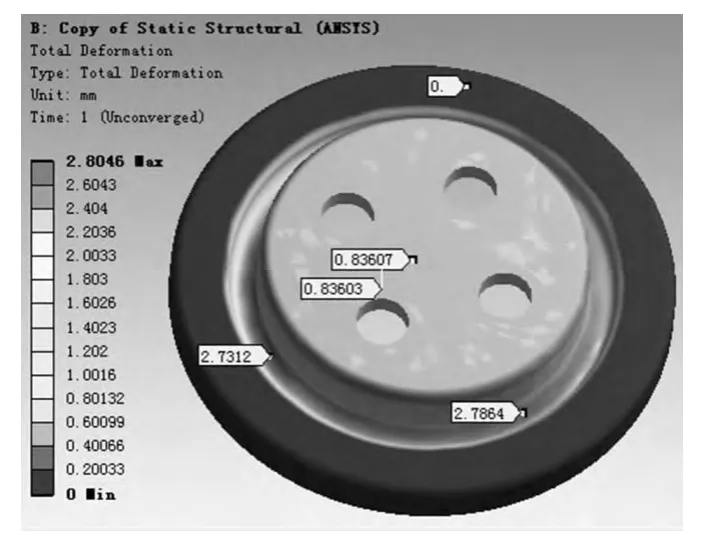
图13 泵膜片在考虑真空度30 kPa 下的位移云图
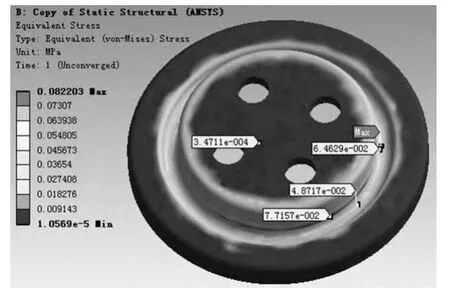
图14 泵膜片在考虑真空度30 kPa 下的应力云图
在当前工况条件下,泵膜片的外表面承受一个标准大气压,内表面受到30 kPa 的真空度压力作用,泵膜片凹槽在气压和拉伸变形共同作用下受到垂直向下的位移为2.8 mm,最大应力为0.08 MPa。由于泵膜片几何尺寸相对偏心量比较大,泵膜片产生的变形范围很小,几乎处于弹性变形区。因此,当偏心量为最大值3 mm时,槽内的最大变形为真空度环境下的位移与偏心时的位移进行矢量叠加。按照等比计算,偏心量为3 mm 时其最大应力为0.28 MPa,其值也远远小于该材料的最大工作压力60 MPa。
4 结论
通过上述计算结果可知,材料为氟橡胶的泵膜片在偏心量为3 mm 的偏心轴带动下,使得气体经过单向阀指定空间产生预定的真空度。其泵膜片承受的最大应力为280 kPa,弹性足够,不会出现破坏现象,能满足实际工作需求,泵膜片设计尺寸可靠。
[1]薛守义.弹塑性力学[M].北京:中国建材工业出版社,2005:51-211.
