水解聚丙烯酰胺溶液松弛时间表征方法研究
2014-11-22吴淑云中石油大庆油田有限责任公司石油勘探开发研究院黑龙江大庆163712
吴淑云(中石油大庆油田有限责任公司石油勘探开发研究院,黑龙江 大庆 163712)
水解聚丙烯酰胺被广泛用于聚合物驱油及复合驱驱油过程中。水解聚丙烯酰胺溶液在孔隙介质中流动的一个重要特性是,中低流动速度下剪切变稀,但在超过某一速度后,聚合物分子在通过一系列岩石体和孔喉时,在流动领域会有拉伸和收缩发生。如果流动速度太高,聚合物分子没有足够的松弛时间去伸展,以适应流动,这种弹性应变导致其表观黏度升高(这种现象通常被称为剪切增稠)。在给定的剪切速率下分子量较高的水解聚丙烯酰胺比低分子量的剪切增稠行为更显著。以往所应用的聚合物分子量较低,这种剪切增稠现象不明显,随着所应用的聚合物分子量的提高,人们意识到剪切增稠行为的重要性。近年来一些学者建立了新的聚合物驱油数学模型。例如,Mojdeh Delshad建立的模型包含了聚合物溶液在孔隙介质中剪切变稀和剪切增稠两部分。其中,剪切增稠部分由宏观流变测量得到的聚合物的分子松弛时间来量化[1~4]。
表征聚合物分子松弛时间的方法有很多,Mojdeh Delshad提出了以下几种聚合物分子松弛时间模型:G′ 与G″交点(G′and G″cross-over point)模型、Rouse模型、珠簧(bead-spring)模型、非线性弹性哑铃(the none-linear elastic dumbell bead)模型、固定频率松弛时间(relaxation time at a fixed frequency)模型和爬杆高度(the rod-climbing height)模型[4]。除了 Mojdeh Delshad提出的这几种聚合物分子松弛时间模型外,Carreau模型和指数模型也可以被用来计算松弛时间[5,6]。
文献报道松弛时间(τ)与聚合物分子量(Μ)的关系为τ∝M3[7]。在现有仪器设备及技术方法的基础上,采用ARES高级扩展流变仪和CaBER毛细管拉伸断裂流变仪对不同分子量及分子量分布的水解聚丙烯酰胺溶液在稳态剪切、动态剪切及拉伸流动试验条件下的黏弹性进行研究,并分别采用不同方法计算其松弛时间。考察不同方法计算的松弛时间随分子量以及分子量分布变化规律,以获得可应用于油田实际的表征方法。
1 试验方法
1.1 剪切流动试验
采用ARES高级扩展流变仪测试水解聚丙烯酰胺溶液(分子量为3×106~39×106)的稳态和动态黏弹性。
1)稳态试验 选用C50/0.04(rad)测量系统,测试在0.001~1000s-1剪切速率范围内溶液的表观黏度和第一法向应力差。
2)动态试验 选用C50/0.04(rad)测量系统,采用振荡(OSC)模式。在固定频率为1Hz下进行应力扫描,确定溶液的线性黏弹性应力区。选择在线性区的应力值进行频率扫描,角频率范围0.01~100(rad/s)。
1.2 拉伸流动试验
采用CaBER毛细管拉伸断裂流变仪测试聚合物溶液的直径随时间的变化曲线。样品直径为6.0mm;原始高宽比为1.0;最终高宽比为4.39;采用线性模式,进行单点拉伸测量。
2 结果与讨论
2.1 稳态试验研究结果
Carreau模型表观黏度与松弛时间的关系为:

式中:μa为表观黏度,mPa·s;μ0为零剪切黏度,mPa·s;τ为松弛时间,s;m 为转变参数;n为曲线斜率;γ为剪切速率,s-1。
图1为采用Carreau模型计算的松弛时间随分子量变化曲线。采用幂律方程对曲线进行拟合,相关系数R2为0.8882,幂律指数为2.0533。
爬杆高度模型表观黏度与松弛时间的关系为:

式中:N1为第一法向应力差,Pa。
图2为采用爬杆高度模型计算的松弛时间随分子量变化曲线。幂律方程拟合相关系数R2为0.9895,幂律指数为0.8996。
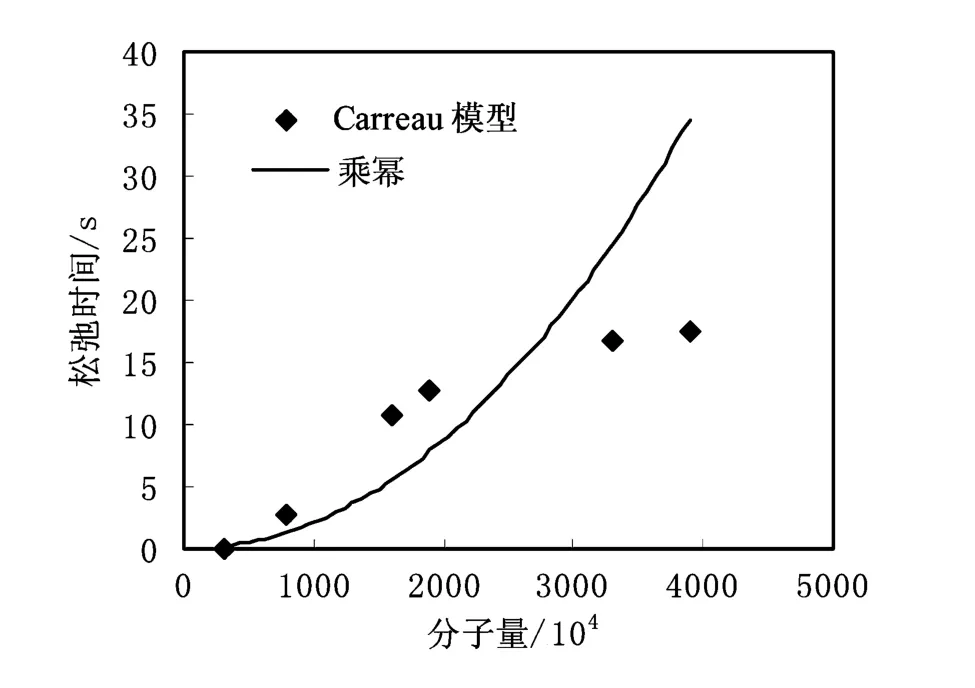
图1 Carreau模型计算的松弛时间随分子量变化曲线

图2 爬杆高度模型计算的松弛时间随分子量变化曲线
图3为Carreau模型对水解聚丙烯酰胺溶液黏度试验数据曲线拟合结果。从图3可以看出Carreau模型能很好拟合水解聚丙烯酰胺溶液黏度试验数据,拟合效果较好。
由于爬杆高度模型只能反映在某一固定剪切速率下溶液体系的松弛时间,其试验结果与文献所报道的聚合物分子量与松弛时间关系(τ∝Μ3)相差较大。与之相比,Carreau模型是对较宽剪切速率范围内试验数据的拟合,因此选择Carreau模型较好。
2.2 动态试验研究结果
图4为水解聚丙烯酰胺溶液动态试验曲线。储能模量G′和损耗模量G″交点所对应频率的倒数称为特征松弛时间。图5为G′和G″交点模型计算的松弛时间随分子量变化曲线。幂律方程拟合相关系数R2为0.9672,幂律指数为3.2325。由于试验样品的不同,在某些聚合物体系的试验曲线中看不到储能模量G′和损耗模量G″交点。下式为固定频率松弛时间模型用于计算一个具有黏性与弹性的流体的表观松弛时间:

式中:G′为储能模量,Pa;G″为损耗模量,Pa;ω为角频率,rad/s。
图6为采用固定频率松弛时间(10rad/s)模型计算的松弛时间随分子量变化曲线。幂律方程拟合相关系数R2为0.9829,幂律指数为0.7493。
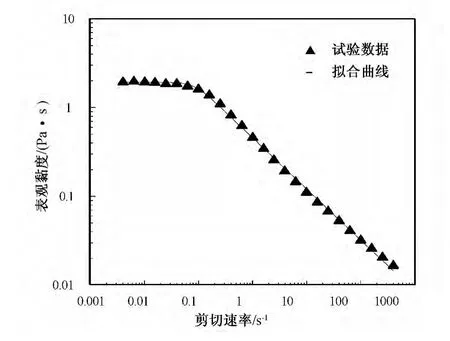
图3 Carreau模型对水解聚丙烯酰胺溶液黏度曲线拟合结果

图4 水解聚丙烯酰胺溶液动态试验曲线
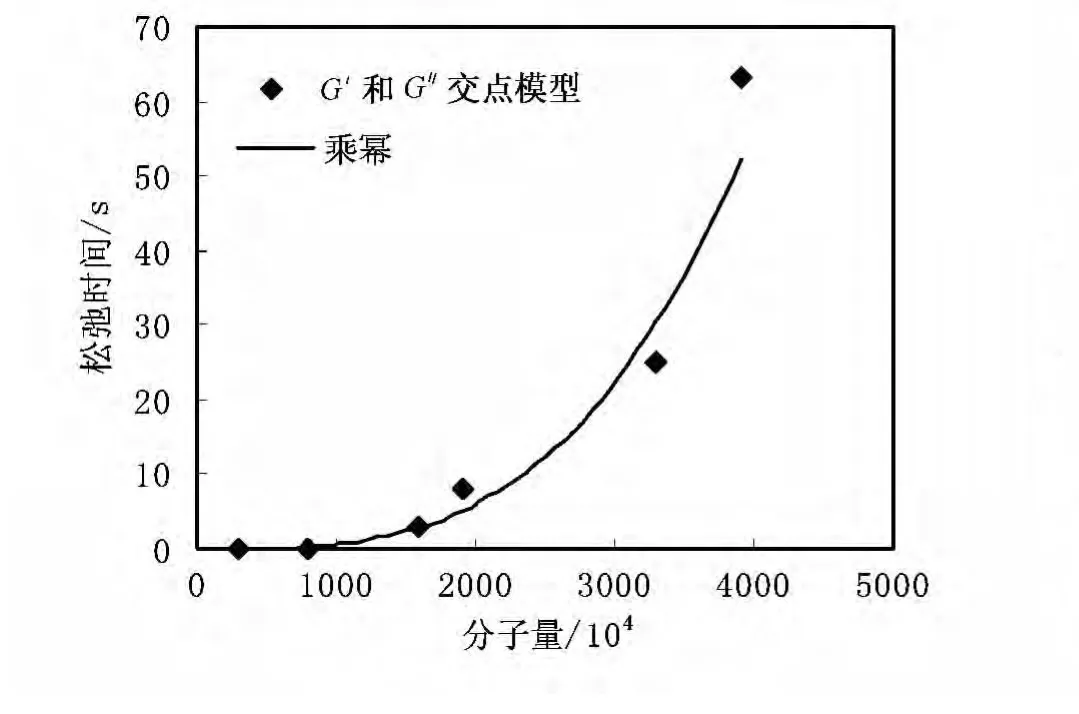
图5 G′和G″交点模型计算的松弛时间随分子量变化曲线
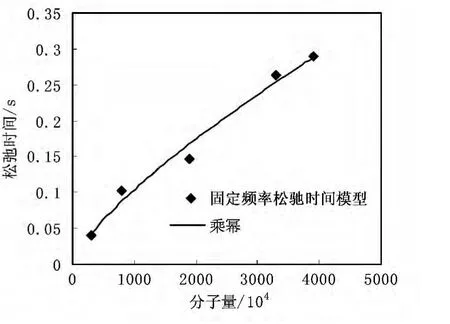
图6 固定频率松弛时间模型计算的松弛时间随分子量变化曲线
与爬杆高度模型相似,固定频率松弛时间模型得到的是在某一固定频率下的松弛时间,其试验结果与文献报道聚合物分子量与松弛时间的关系(τ∝Μ3)相差也较大。由储能模量G′和损耗模量G″交点得到相应的特征松弛时间,该交点可以被用来描述分子相互缠绕现象的开始。因此,G′和G″交点模型计算的结果较好。
2.3 拉伸试验研究结果
指数模型弹性模量与松弛时间的关系为:

式中:G为弹性模量,Pa;D0为样品直径,mm;Dmid为流体丝中间直径,mm;σ为表面张力,mN/m。
图7为指数模型对拉伸试验曲线拟合结果。由图7可以看出指数模型可以较好地描述水解聚丙烯酰胺溶液拉伸试验结果。图8为采用指数模型计算的松弛时间随分子量变化曲线。幂律方程拟合相关系数R2为0.9898,幂律指数为1.7445。
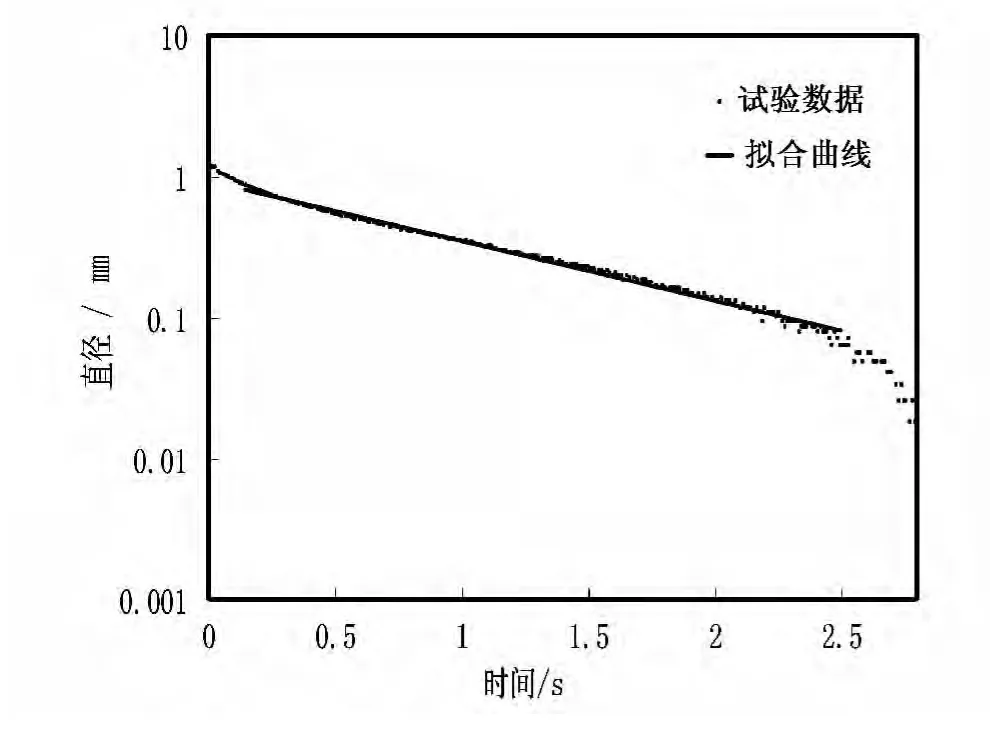
图7 指数模型对拉伸试验曲线拟合结果
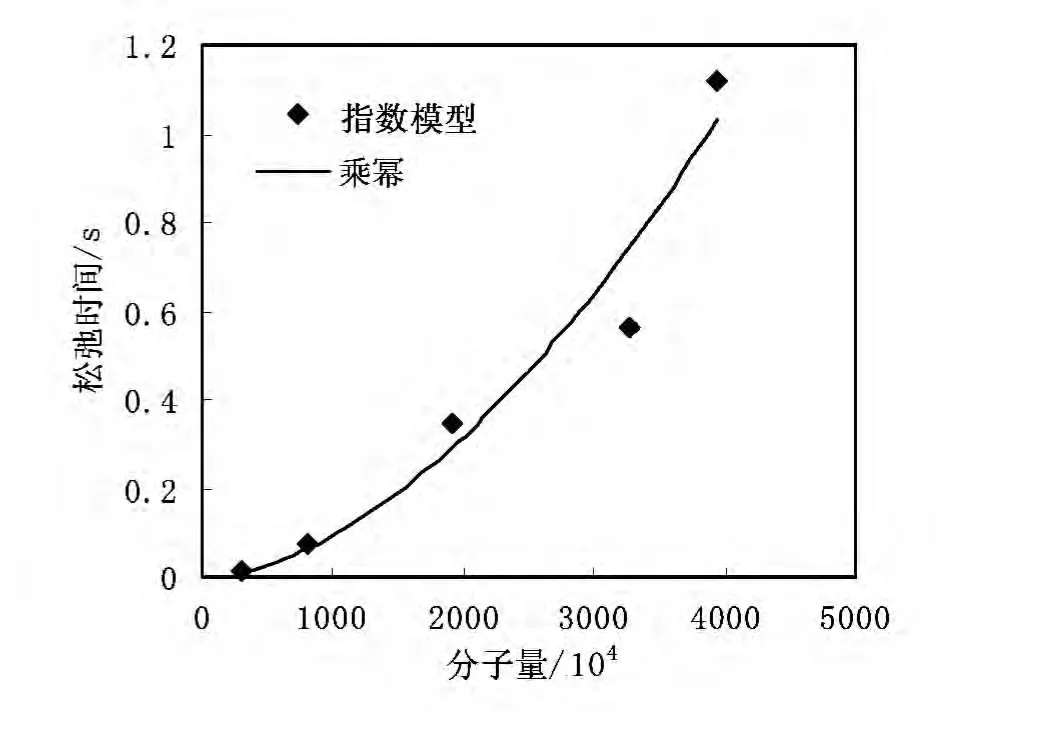
图8 指数模型计算的松弛时间随分子量变化曲线
2.4 模型的筛选
为进一步考察G′和G″交点模型、Carreau模型和指数模型的应用效果,分别采用这3种模型计算不同分子量分布聚合物溶液的松弛时间,结果列于表1。

表1 不同模型计算的不同分子量分布聚合物溶液松弛时间
从表1可以看出,Carreau模型计算的松弛时间随聚合物分子量分布宽度(用多分散系数表征)的增加基本没有变化;G′和G″交点模型计算的松弛时间随聚合物分子量分布宽度的增加出现最大值;指数模型计算的松弛时间则随分子量分布宽度的增加而增大。因为与剪切流动试验相比,采用CaBER毛细管单轴拉伸试验方法在检测分子量分布宽度时更加敏感,并且CaBER单轴拉伸试验方法操作更加简单。因此根据油田实际情况,采用指数模型来表征水解聚丙烯酰胺溶液的松弛时间较合适。
3 结论
1)所有方法得到的松弛时间都与分子量成正比。G′和G″交点模型得到的结果与文献关于聚合物分子量与松弛时间的关系(τ∝M3)最接近,其次是Carreau模型和指数模型。
2)Carreau模型计算的松弛时间随聚合物分子量分布宽度的增加基本没有变化;G′和G″交点模型计算的松弛时间随聚合物分子量分布宽度的增加出现最大值;指数模型计算的松弛时间则随分子量分布宽度的增加而增大。
3)与剪切流动试验相比,采用CaBER毛细管单轴拉伸试验在检测分子量分布时更加敏感,并且操作非常简单,因此根据油田实际采用指数模型来表征水解聚丙烯酰胺溶液的松弛时间较合适。
[1]王启民,冀宝发,隋军,等 .大庆油田三次采油技术的实践与认识 [J].大庆石油地质与开发,2001,20(2):1~8.
[2]王德民 .发展三次采油新理论新技术,确保大庆油田持续稳定发展(上)[J].大庆石油地质与开发,2001,20(3):1~7.
[3]陈国,赵刚,马远乐 .黏弹性聚合物驱油的数学模型 [J].清华大学学报,2006,46(6):882~885.
[4]Delshad M.Mechanistic interpretation and utilization of viscoelastic behavior of polymer solutions for improved polymer-flood efficiency[J].SPE113620,2008.
[5]Lucy E R,Timothy P S,Justin J C,et al.Influence of the molar mass distribution on the elongational behavior of polymer solutions in capillary breakup [J].Applied Rheology,2005,15(1):12~27.
[6]Plog J P,Kulicke W M,Clasen C.Capillary break-up rheometry of low-viscosity elastic fluids [J].Applied Rheology,2005,15(1):28~37.
[7]巴勒斯 H A,赫顿J H,瓦尔特斯K.流变学导引 [M].吴大诚,等译 .北京:中国石化出版社,1992.58~59.
