变压器调压区均压环的设计与优化

2014-11-22梅文哲范小辉黄郑宇

电力工程技术 2014年4期

梅文哲，赵建，范小辉，黄郑宇

(苏州供电公司，江苏苏州 215000)

变压器作为电力系统传输电能的核心部件，其正常稳定运行极具重要性。调压区是变压器中完成电压调节的重要区域，随着电压等级的攀升，调压区的电场环境更加恶劣。通常情况下，调压区分接开关电极的不规则形状，金具结构会导致高压电极和接地端附近电位的快速衰减，在临近高压电极和接地端处产生较高的电场。长期运行中容易导致局部放电，引起局部油温升高和油的裂解，加速绝缘油的热老化及击穿，成为了变压器运行的重大隐患。优化其电场分布对整个变压器的安全运行起着非常关键的作用。

在调压区安装均压环改善其电场分布。均压环的作用主要是降低调压区内某些部位（比如套筒）和两端金具表面过高的电位梯度，可以将最大场强从高压电极与接线端金具转移到保护环的外侧，最大场强值也会显著降低，电场分布趋于均匀。另外，均压环还有引弧、防止金具表面放电、漏电起痕及电腐蚀，并且能消除沿面放电引起的绝缘油老化[3]。因此，采用均压环改善调压区电场和电位分布具有重要的工程和学术意义。均压环的尺寸、安装位置等参数的确定以及方案的最优化是至关重要的。通常采用的分步优化只是一种局域优化方法，具有一定的局限性。为实现多参数多输出量下的优化设计，试图探索合适的优化方法，拟采用神经网络方法及最优化理论进行其全局优化设计。

1 带均压环调压区电场分布的计算

1.1 有限元计算模型的确定

根据实际结构特点，在仿真之前，从工程的角度进行如图1、图2 所示简化。

均压环、电极、套筒和垫片等合起来组成的系统场域是一个有界的三维电场，使用有限元法进行电场分布计算[2]。得到调压区电场的计算方程和边界条件。

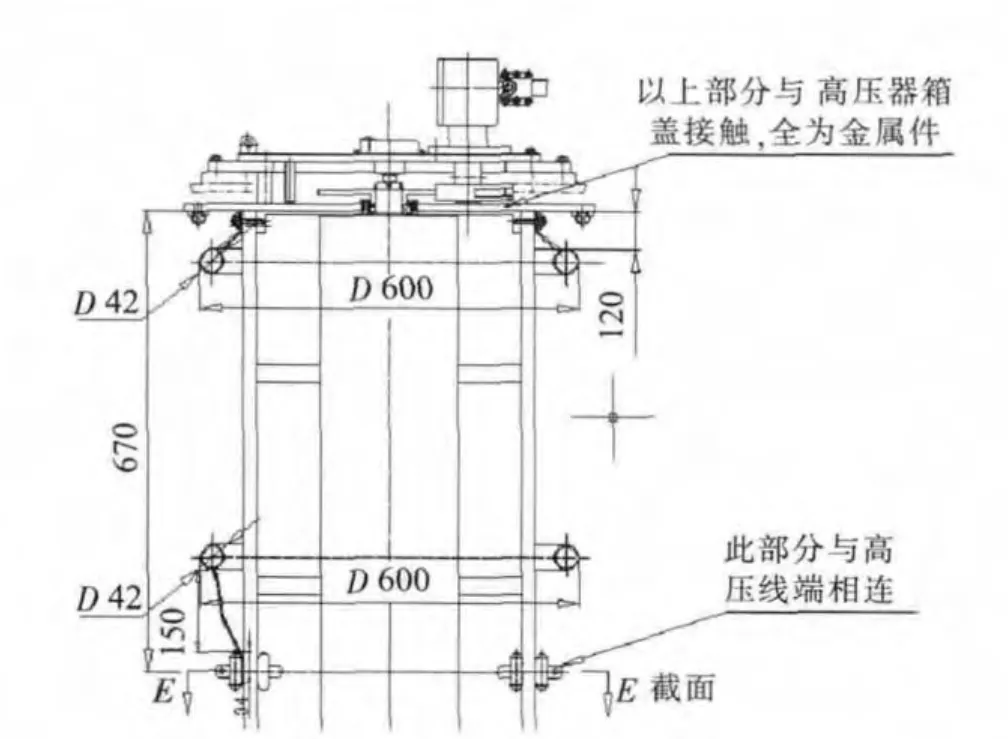
图1 变压器调压区结构示意图

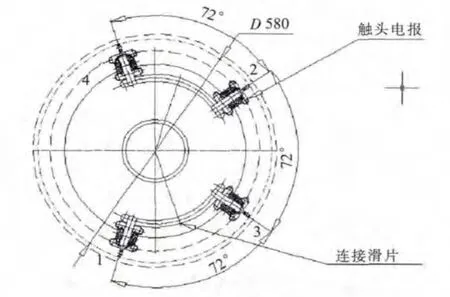
图2 调压区剖面结构示意图

（1）计算区域内电位满足Laplace 方程：

（2）变压器箱盖及低压端均压环表面电位满足：

（3）高压触头及高压端均压环表面电位满足：

（4）介质分界面上满足：

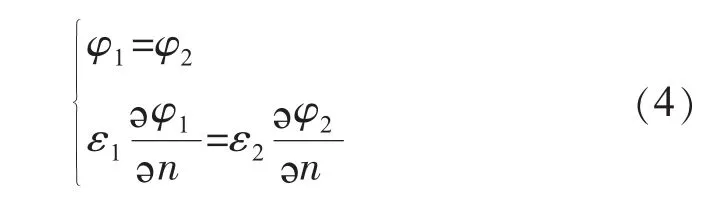
调压区有限元模型如图3 所示。

图3 变压器调压区的有限元模型

1.2 计算结果

以均压环的结构尺寸（环径r，管径D，均压环间距H，低压端均压环与接地板间距H1）为参数分析其值选取对调压区电场分布的影响。首先设定均压环各参数范围，如表1 所示。

表1 仿真中均压环的参数设置 mm

当均压环参数值取r=272 mm，D=22 mm，H=318 mm，H1=168 mm时，得到了一组仿真结果，包括高、低压端均压环电场，变压器端盖电场，内、外绝缘筒电场分布情况。由仿真结果分析可发现，绝缘圆筒的表面最大场强远低于高、低压均压环及接线端金具的表面最大场强，故在分析中以均压环及接线端金具的表面最大场强最小为目标，重点考虑通过改变均压环的结构尺寸及安放位置来实现电场最优分布。

2 均压环的常规分步优化设计

将探索在均压环参数设计的2 种不同的优化方式（常规的分步优化方式[2-10]和神经网络最优化方式[11]）对电场分布最终结果的影响。在均压环设计中多采用分步优化的方法，即每次先确定一个参数作为优化变量，其余为定值，进行目标函数的求解。根据不同参数下目标函数取值的大小，断定所选参数对目标函数的影响。这种分步优化的方法可以缩小优化变量的取值范围，并了解其与目标函数可能存在的规律。现依次选取环径r，管径D，均压环间距H，低压端均压环与端盖间距H1作为分步优化变量，探究其各自取值与调压区电场分布的关系。得到的r，D，H，H1与调压区电场分布关系如图4—7 所示。

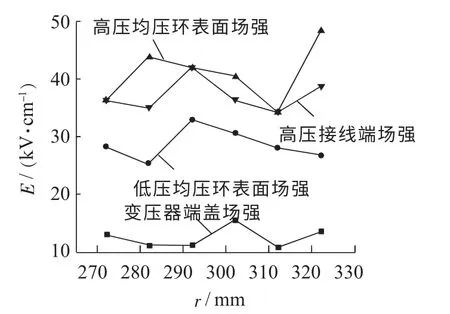
图4 均压环环径改变对电场分布的影响

图5 均压环管径改变对电场分布的影响

图6 均压环间距改变对电场分布的影响

图7 低压端均压环与箱盖间距改变对电场分布的影响

分步优化虽然可以明确反映均压环不同参数对电场分布的影响，但是这些参数的组合并不是一组准确的最优参数，即它们只是近似或局部最优解。这是由于均压环结构参数与调压区电场分布之间是一个非线性的关系，无法简单的利用各参数的局部最优值组合出所有参数的全局最优值。

3 均压环结构参数的神经网络优化设计

随着电压等级不断攀升，对电场环境的严格要求显然需要更加优良的优化方法。为获得最优化解，提出通过神经网络构建均压环参数—调压区电场的输入—输出模型，利用最优化方法构建优化算法，并利用程序语言实现来完成变压器调压区均压环结构参数的优化设计。均压环参数优化设计的目标就是求取一组r，D，H，H1的值，使得E1与E2取得最小值。然而，r，D，H，H1与E1，E2之间的关系是一种多维非线性关系，这种关系很难用简单函数直接给出。通过让神经网络学习和训练，就可以得出隐含输入／输出数据关系的非线性映射模型。这种模型可以逼近输入和输出之间的多维非线性特性，从而建立输入与输出之间的关系。

为了利用神经网络建立r，D，H，H1和E1，E2之间的映射关系，采用如前所述的有限元方法计算出一些样本供神经网络训练和验证使用，再由已建立的神经网络模型计算出各结构参数变化下的E1，E2，根据合适的算法从中找出满足优化目标的均压环的最优结构参数。

3.1 均压环结构参数神经网络优化模型

调压区电场分布与均压环结构参数之间满足如下映射关系：

这里采用三层前馈式神经网络来构建均压环优化模型，网络的输入为均压环环径、管径、均压环间距和低压端均压环与端盖间距。网络的输出为高、低压端均压环表面最大场强。其结构如图8 所示。

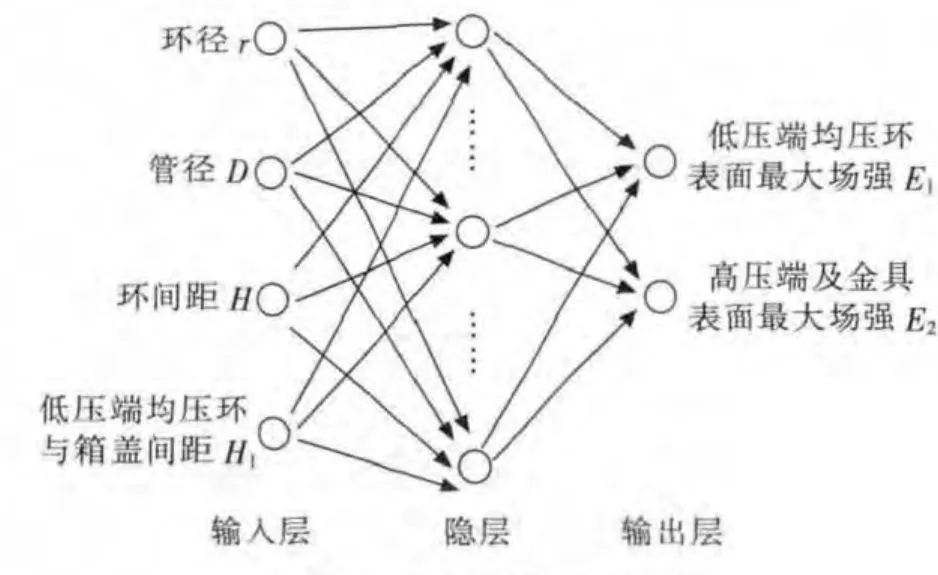
图8 神经网络模型结构

3.2 神经网络模型构建

为了使网络模型快速收敛，按下式进行归一化的处理：

网络输入层与隐含层的传递函数取为log[s（x）]，隐含层与输出层的传递函数取为tan[s（x）]。通过反复试验对比，网络隐层神经元个数取为13个。网络训练算法取为L-M 方法，则：

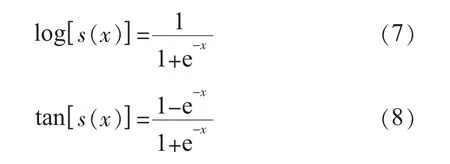
3.3 均压环参数最优化方法的研究

最优化方法是指在给定的约束条件下，构建问题的数学模型并确定目标函数，找出决策变量的值，使得目标函数达到最小或最大值。这里构建的神经网络模型有2个输出变量。当均压环参数变化时，对应的2个输出(高、低压均压环表面最大场强)均会变化。在均压环结构参数的优化设计中，由于输入输出模型的非线性性，无法简单的通过诸如E1+E2和E1-E2之类的简单函数作为寻求最优解问题的目标函数，如图9 所示。而且由于神经网络的双参数输出，与以往的均压环结构参数的神经网络优化设计相比又存在特殊性。如何在双参数输出的情况下，通过合适的算法寻求到均压环结构参数的全求解域最优解是优化设计的关键。对于不同的结构参数输入，通过神经网络可以得到相应的电场强度输出。将均压环结构参数r，D，H，H1依次在[302，322]，[32，42]，[318，358]和[118，168]区间内都以l为步长变化（单位mm），作为输入向量，通过神经网络模拟输出。

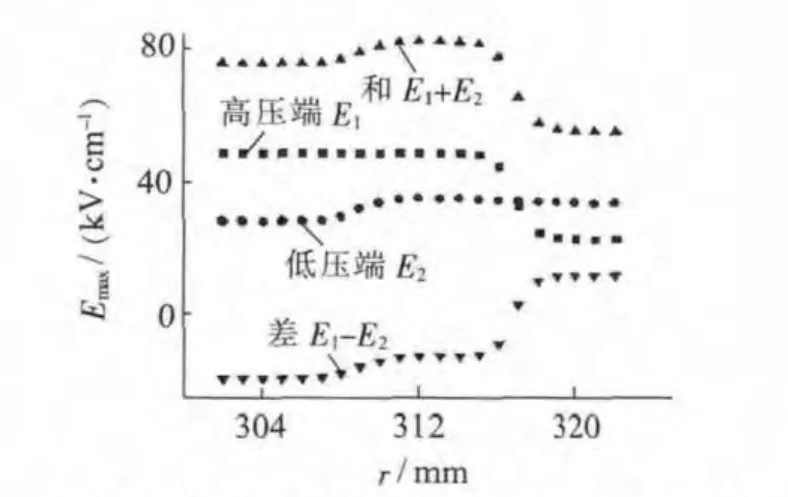
图9 改变r 对电场分布及简单目标函数E1+E2和E1-E2的影响

基于最优化理论，得到的目标函数算法和最优化求解模型。

目标函数：min[max（E1，E2）]

约束条件：x∈S

其中S为输入向量x的可行域（Feasible Region可取值集合）。E1，E2分别为高低压端均压环表面最大电场输出向量。采用方法max（）比较E1和E2返回较大值作为输出向量元素。同时采用方法min（）寻找输入向量的最小值，返回其寻获值及对应结构参数。利用程序设计方法实现算法后，得到的最优化结果：均压环环径r=322 mm；管径D=42 mm；均压环间距H=357 mm；低压端均压环与端盖间距H1=166 mm。此时，高压端均压环表面最大场强E1=27.416 9 kV/cm，低压端均压环表面最大场强E2=23.559 4 kV/cm。