二维弱奇异积分高精度数值求积公式的构造
2014-11-21宁德圣
曾 光, 黄 晋, 雷 莉, 宁德圣
(1. 东华理工大学理学院,江西 南昌 330013;2. 电子科技大学数学科学学院,四川 成都 611731)
考虑二维弱奇异积分

这类积分来源于大量工程问题诸如弹性力学、断裂力学等问题中。其中寻找有效,精度高的数值方法求解弱奇异积分和弱奇异积分方程成为计算数学领域的研究热点之一(阮周生等,2010;Lifanov et al.,2004;Sidi et al.,1988;Lyness et al.,1967)。对于各类一维奇异积分与奇异积分方程的计算已有很多学者做了大量的工作,主要包括配置法和有限元Galerkin 方法,这是由Sloan 等(1988)提出的,配置法是对非奇异部分用一组正交基的线性组合表示,然后用配点求积来处理,每个离散元素需要计算一重奇异积分;有限元Galerkin 方法对非奇异部分的处理跟配置法相同,即用一组正交基线性表示,然后取内积,每个离散元素需要计算二重奇异积分。这两种方法存在一些不足:①需要处理奇异积分;②计算量大,精度低;③很难得到误差的渐进展开式和后验误差估计。此外还有Duffy 变换消去法和奇异减方法:这是由Atkinson(1989,1997)提出,Duffy 变换消去法是利用该变换把区间的奇异性转化到端点部分进行计算,不过同样存在端点的超奇异性计算;奇异减方法的不足:虽然奇异消去了,但却产生了一个高阶函数项和一个已知的奇异部分,仍然存在着一个奇异部分的计算。
为了克服以上方法的不足,本文主要工作是基于欧拉—麦克劳林展开式和Sidi 推导出的一维弱奇异积分的求积公式基础上,推导出了二维弱奇异积分的求积公式及其误差的渐进展开式,此类求积公式只需赋值,不需计算二重积分。因此,计算量小,同时收敛阶大为提高。利用这类积分公式进行计算可以得到十分精确的结果。这为后面讨论多维弱奇异积分方程奠定了坚实地基础。
1 主要结论
为方便后面讨论,先给出几个定义:
定义 2.1(b)(Choi et al.,2004).


令h = (b -a)/m,xj= a +jh(j = 0,1,…,m),
下面给出本文主要结论证明需用到的引理。
引理2.2 (Sidi et al.,1988)假设g(x)在[a,b]上2l 阶可微,且1.和则当h→0 时,误差的渐进展开式为

其中

是一维弱奇异积分的求积公式,B2μ是Bernoulli 数以及ξ(τ)是Riemamn zeta 函数,E(h)= I(g)-Q(h)。
推论2.3 假设g(x)在[a,b]上2l 阶可微,G(x)是周期为b-a 的周期函数。且G(x)在(-∞,上2l 阶可微。则当h→0 时,误差的渐进展开式为

其中

是一维弱奇异积分的求积公式,B2μ是Bernoulli 数以及ξ(τ)是Riemamn zeta 函数。
定理2.4 假设f(x,y)在区域[a,b]×[c,d]内有直到2l 阶偏导数存在,令 F(x,y) =
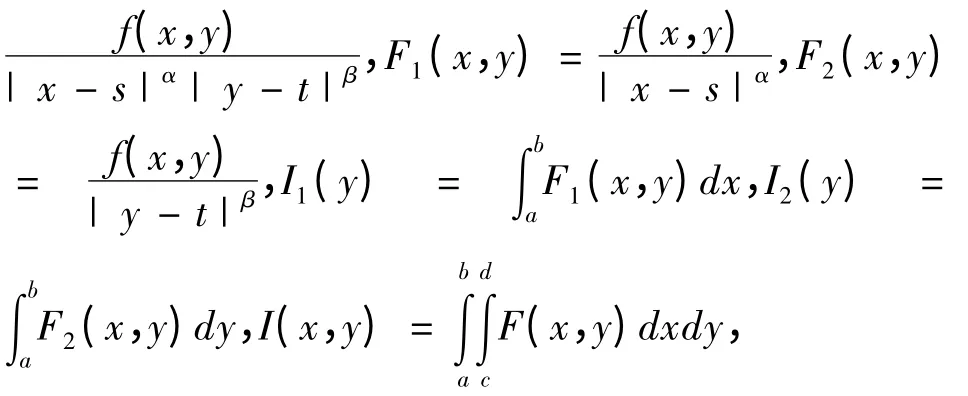
0 <α,β <1.则有误差的渐进展开式


其中
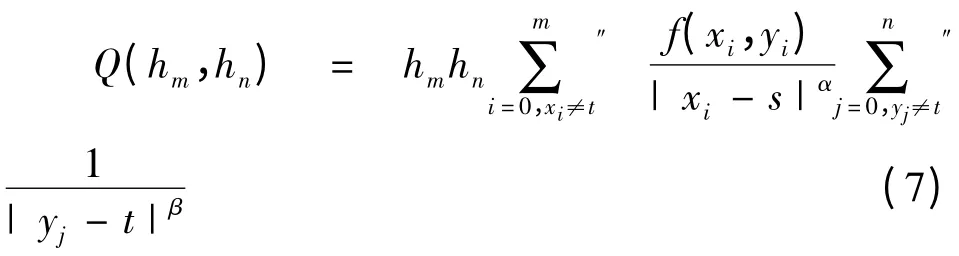
是 二 维 弱 奇 异 积 分 的 求 积 公 式,B2μ是Bernoulli 数及ξ(τ)是Riemamn zeta 函数,h =max{hm,hn},同时

证明:根据定理2.2,可以推导出


则

下面分别计算出Pi,i = 1,2,3,4.首先

其中,

这里,

下面求P13,P14

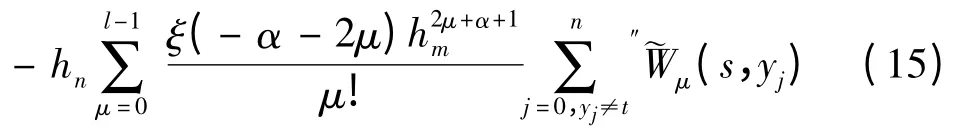
其中

下面计算P2,P3,


同时,

根据公式(12,13,15,17 ~20),完成了此定理的证明。
3 结语
积分方程数值解中的一类很重要的数值方法——机械求积法的关键是求积公式的构造,本文主要基于欧拉—麦克劳林展开式及A. Sidi 和M.Israeli 推导出的一维弱奇异积分的求积公式基础上,推导出了新的二维弱奇异积分求积公式及其误差的渐进展开式,此类求积公式只需赋值,不需计算二重积分。因此,计算量小,同时收敛阶大为提高到。因此,利用这类积分公式进行计算可以得到十分精确的结果。这为后面讨论多维弱奇异积分方程奠定了基础。
阮周生,孙海. 2010. 同伦摄动法在一类线性积微分方程初值问题中的应用[J]. 东华理工大学学报:自然科学版,33(3):298-300.
Atkinson K E.1989. An Introduction to Numerical Analysis[M]. 2nd edn. Wiley&Sons.
Atkinson K E.1997. The Numerical Solution of Integral Equations of the Second Kind[M]. Cambridge University Press.
Choi U J,Kim S W,Yun B I. 2004. Improvement of the asymptotic behavior of the Euler-Maclaurin formula for Cauchy principal value and Hadamard finite-part integrals[J]. Int. J. Numer. Meth. Engin.,61:496-513.
Lyness J N,Ninham B W. 1967. Numerical quadrature and asymptotic expansions[J]. Math. Comp.,21:162-178.
Lifanov I K,Poltavskii L N,Vainikko G M.2004. Hypersingular Integral Equations and Their Applications[M]. ACRC Press Company.
Sidi A,Israeli M. 1988. Quadrature method for periodic singular and weak singular Fredholm integral equations[J]. J Sci. comp.,2:201-231.
Sloan I H,Spence A.1988. The Galerkin method for integral equations of first-kind with logarithmic kernel:theory[J]. IMA J. Numer. Anal.,8:105-122.
