自适应抗干扰通信系统中频谱感知技术研究

陈 蕾，姚远程，秦明伟

(西南科技大学信息工程学院特殊环境机器人技术四川省重点实验室，四川绵阳621002)

随着无线通信技术的迅猛发展，日益增长的频谱需求和有限的频谱资源之间的矛盾日益突出，造成频谱资源利用率低下。研究表明，目前适宜无线通信业务的频谱资源一方面十分稀缺，一方面又浪费严重。频谱资源的紧张不是因为物理上的可用频谱资源的缺少造成，而是由于不合理的频谱资源管理政策造成。认知无线电技术作为一种智能的无线通信系统，它能够通过感知外部频谱环境，自适应调整系统的参数，如载频、带宽、传输功率和调制方式等，实现频谱的再利用，可显著提高频谱的利用率。因此，频谱感知作为认知无线电中最关键的技术，如何快速、准确地检测出频谱空洞是非常重要的。

自适应抗干扰通信系统与传统通信系统相比，体制不再是固定不变的，其核心是在信号发射时，发射机能够根据通信环境的变化及信道的干扰情况，自动选择工作频率、数据速率和调制模式，保证在一定的误码率条件下，充分利用信道容量，提高频谱利用率和通信系统的抗干扰能力［1］。采用自适应技术，可以在信道条件好的时候，提高频谱利用率，避免因单一的调制技术而导致对信道容量利用不足，在信道干扰严重时，也可以保证最低的通信能力，具有很大的研究价值。

认知无线电中的频谱感知方法有很多，比如感知技术中的发射机检测，就包括匹配滤波法、能量检测法以及循环平稳特征检测方法，三种方法各有优缺点，对于不同的频谱环境，针对不同的授权用户，能适用的最佳频谱检测方法也有所不同。由于在大部分的环境下，检测信号的信息以及所处的环境都属于未知，无法获得先验信息，所以一般采用能量检测算法。能量检测是Harry Urkowitz1967年提出的检测方法，它利用接收信号的能量或者功率大小来判断是否有待检测的信号存在。这种方法是一种对未知参数的确定性信号存在性检测的有效方法，这种算法复杂度较低，实施简单，同时不需要任何先验信息，因此被认为是认知无线电系统中最通用的感知算法。

1 能量检测原理

对任何的频谱感知技术而言，最终的目的都是检测特定频段内是否存在信号。能量检测利用接收信号的能量来判断是否有待检测的信号存在，如果接收到的能量大于预先设定的阈值，判定有信号的存在;否则，判定只有噪声存在。通常用检测概率、虚警概率、漏检概率等指标来衡量系统的检测性能，虚警概率是指主用户信号不存在，检测器判定信号存在的概率。检验概率是指主用户信号存在时，检测器判定信号存在的概率。漏检概率是指主用户存在，检测器判定信号不存在的概率。通过检测概率与虚警概率之间的关系曲线，即ROC曲线(Receiver Operating Characteristic Curve)，可以很好地反映出频谱检测的性能［2］。

1.1 基于时域的能量检测算法研究

在时域上分析，如图1所示，将接收到的信号经过带通滤波器，取出感兴趣的频段，经模数转化器、平方器、累加器进行能量计算，最后与预先设定的阈值进行比较作出判决。

图1 基于时域分析的能量检测算法流程图

设加性高斯白噪声(Additive White Gauss Noise，AWGN)信道下，认知用户接收信号的二元假设检测模型表示为［3］

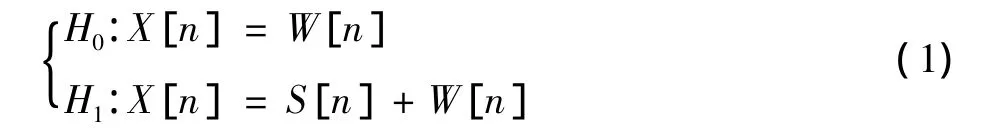
式中:S［n］和W［n］分别是信号和噪声的抽样值，n为检测时信号的抽样数目。取检验统计量Y为

式中:参数N代表观测时长，通过将检验统计量Y和设定阈值比较得出特定频段是否有信号存在。这里假定高斯白噪声均值为0、方差为。能量检测算法中，检验统计量Y具有如下分布

式中:Γ(·)表示完整的Gamma函数;Q(·)为广义MarcumQ函数。检验概率是关于信噪比的函数，而虚警概率与信噪比无关，只与噪声和门限取值有关。

1.2 基于频域的能量检测算法研究

如图2所示，首先将接收到的时域信号进行快速傅里叶变换将信号从时域变换到频域，然后对频域信号进行求模平方，再累加求和并除以FFT分析点数N。

图2 基于频域分析的能量检测算法流程图

当在一个检测周期内，对认知用户接收到的信号进行采样，可将前面假设的二元模型变换为

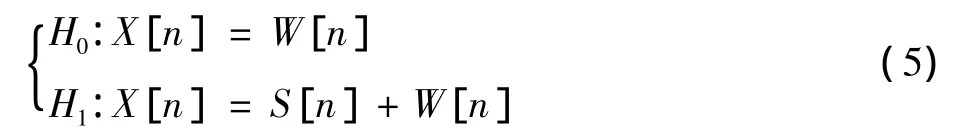
式中:X［n］是接收到的信号;S［n］是能量为的主用户信号采样值的FFT;W［n］是均值为0、方差为的加性高斯白噪声采样值的FFT。检验统计量Y为

由上面分析可知，检验统计量Y在信号存在和不存在的情况下，分别服从自由度为N的卡方分布和非中心卡方分布。设采样数为N，当采样数N比较大的时候，可以根据中心极限定理，得到检验统计量Y近似服从如下高斯分布

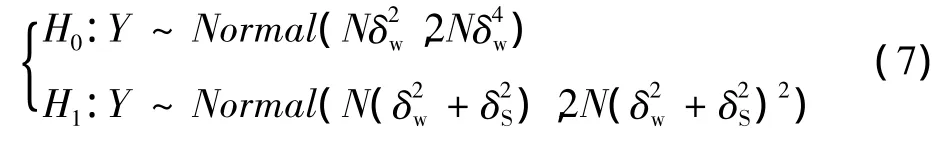
设定判决门限为λ，因为Y近似服从高斯分布，则虚警概率Pf和检测概率Pd分别可以写为

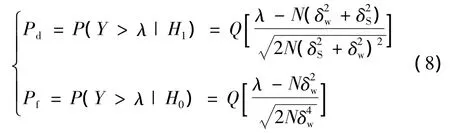
由虚警概率的公式，可以反推出判决门限λ的表达式，在期望目标虚警概率、白噪声方差，取样数N都已知的情况下，可以计算出门限值，这就是奈曼—皮尔逊准则［4］。

2 能量检测算法的性能评估

2.1 算法提出

由以上两种算法可知，门限值的设定只和虚警概率和噪声功率有关。在设定虚警概率时，需要考虑虚警概率和检验概率之间的一个平衡。从图3可以看到在虚警概率一定时，增加信噪比，检验概率会逐步增加，使检测性能得到提升。图4显示当信噪比一定时，检验概率会随着判决门限增大而减小，过低的检测概率表示检测不到授权用户信号的概率较高，从而导致强行占用授权用户使用频段的现象发生，对授权用户产生干扰;虚警概率也会随着判决门限的减小而增大，过高的虚警概率会使认知用户成功检测到频谱空洞的概率下降，从而使频谱利用率下降，造成不必要的频谱资源浪费。可见，不同的信噪比以及判决门限的选择都会对检验性能造成影响，为了避免固定门限值造成的误差，本文选择奈曼—皮尔逊准则动态选择判决门限，并对不同信噪比和采样点数下的仿真性能进行了研究。

图3 不同信噪比下ROC

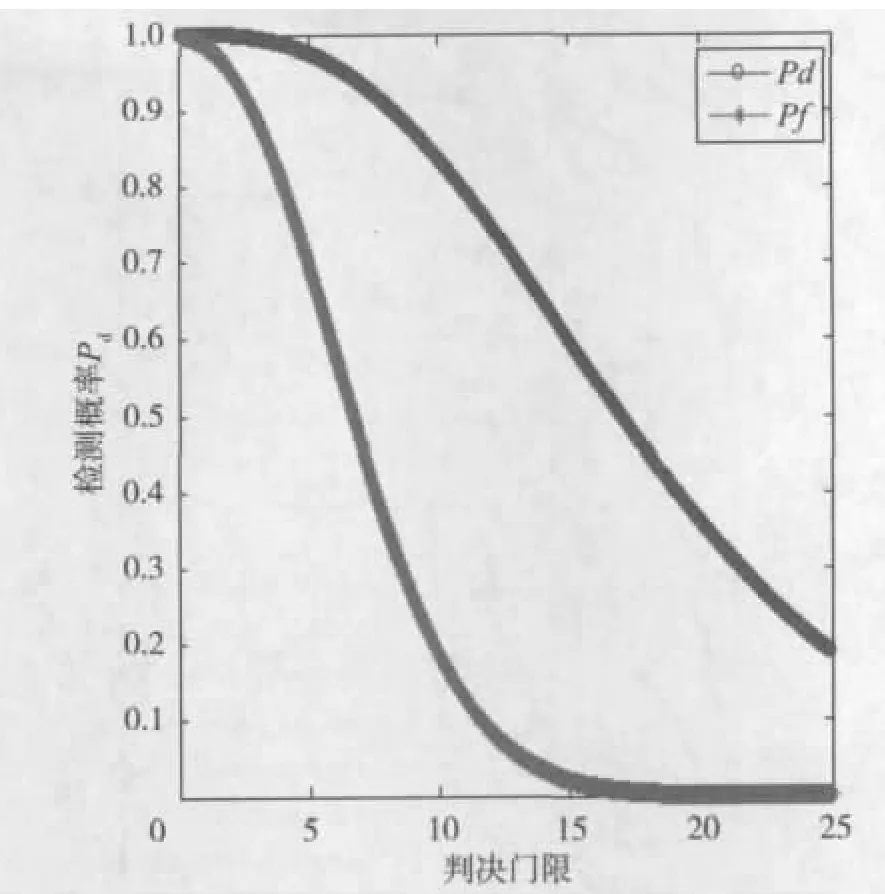
图4 不同判决门限的检测性能

2.2 能量检测模型的建立

在Simulink中进行建模仿真［5］，如图5所示，仿真模型由主用户信号发生器，传输信道和次用户信号接收器三大部分组成。首先，主用户信号进行传输，通过特定的仿真信道，进行滤波，得到感兴趣的频段，通过时域或频域的能量计算，得到检验统计量。另外，根据事先估计的噪声功率和虚警概率，由奈曼—皮尔逊准则，计算出门限阈值，与检验统计量进行比较，若大于门限阈值，则判定信号存在，将检测结果设为1;反之，信号不存在，检测结果设为0。次用户根据得到的判决结果判断是否有信号存在，再决定是否接入频段。仿真结束，可得到检验概率［6］为

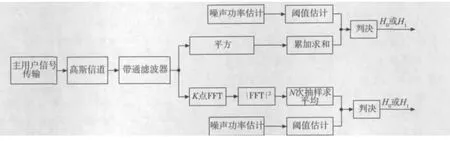
图5 两种能量检测算法模型

为了验证能量检测算法频谱感知功能的可行性，文章采用蒙特卡罗方法进行仿真，通过设定仿真次数N，构建仿真模型。假设授权信号为DPSK调制信号，通过设定不同的信噪比来检验系统的感知性能，同时对理论仿真结果和实际仿真结果进行比较。信道为高斯信道，设定虚警概率由0到1变化，由奈曼—皮尔逊准则，可计算出动态理论判决门限，由第2节理论知识可知，统计判决门限服从卡方分布。根据时域的能量计算公式得出信号的累计接收功率，与统计判决门限进行比较，得出判决结果。N次仿真结束，根据统计到信号存在的次数，可计算出检验概率，如图6所示。

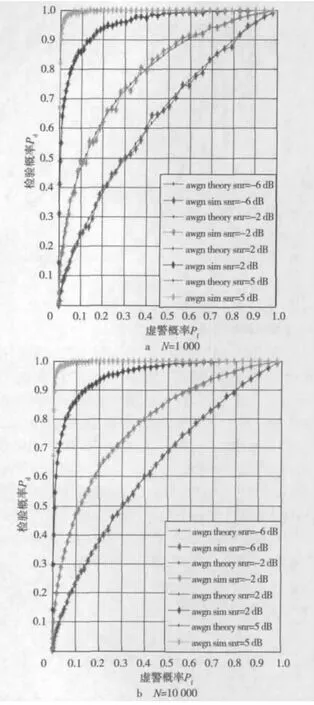
图6 不同仿真次数下的理论仿真和实际仿真比较

图6a显示在仿真次数N=1 000时，信噪比分别为－6 dB，－2 dB，2 dB以及5 dB情况下，实际仿真和理论仿真的检验概率变化。图6b显示在仿真次数N=10 000时，信噪比相同变化情况下，实际仿真和理论仿真的检验概率变化。由图可知实际仿真与理论仿真结果近似重合，说明研究的理论信道可以模拟现实中遇到的衰落信道。对比发现，仿真次数对信道的仿真非常重要，直接关系到检测的准确性，随着仿真次数的增加，系统检测准确性更高，相同仿真次数下，随着信噪比的增加，系统检验性能提高。如果要达到系统识别率大于95%，在低信噪比下，虚警概率会很高，比如在信噪比为－2 dB时，虚警概率要大于0.7才能达到要求。同样指标下，信噪比越高，虚警概率越低，这样认知用户成功检测到频谱空洞的概率越高，能迅速提高系统的频谱利用率。

3 小结

本文针对自适应抗干扰系统中的频谱感知技术进行了一些初步的探索，选择能量检测算法进行频谱感知，在MATLAB－Simulink平台下进行能量检测算法建模仿真。从理论和仿真两个方面针对能量检测性能评估方法进行了研究，提出信噪比和仿真次数对检测性能的影响，同时选用奈曼—皮尔逊准则来动态调整判决门限，可提高系统整体检验性能。能量检测算法简单易行，但是在实际环境中，由于受外界环境影响，方差在一定范围内波动，造成噪声不确定性的影响［7］，这样对认知用户可能存在不可检测的现象。所以在接下来的工作中，会针对更多的频谱感知方法进行研究，并对能量检测算法中存在的问题进行改进。

［1］李杨.自适应卫星通信系统方案及相关技术研究［D］.北京:中国科学院研究生院，2005.

［2］王锴.基于能量检测的认知无线电协作检测算法研究［D］.哈尔滨:哈尔滨工业大学，2010.

［3］ AKYILDIZ F，WON－YEOL L，MEHMET C，et al.A survey on spectrum management in cognitive radio networks［J］.IEEE Communication Magzine，2008，46(4):40－48.

［4］ QING Z，BRIAN M S.A survey of dynamic spectrum access［J］.IEEE Signal Processing Magazine，2007，24(3):79－89.

［5］ ARAVIND H，GANDHIRAJR，SOMAN K P，et al.Spectrum sensing implementations for software defined radio in Simulink［J］.Procedia Engineering ，2012(30):1119－1128.

［6］ DANIELA M，MARTíNEZ P.Evaluation of energy detection for spectrum sensing based on the dynamic selection of detection－threshold［J］.Procedia Engineering，2012(35):135－143.

［7］ URKOWITZ H.Energy detection of unknown deterministic signals［EB/OL］.［2013－06－01］.http://wenku.baidu.com/link?url=L2m SOYKdwMwcreIs7LfCfvIY3b7jObuHlm4tqHJgjM2msu9LnIPcF27yQt_XG jfpVQZNA73－SGu410FsSQPuJPCe9s5mrTz7QNfYkKuqv13.