基于FPGA的FIR滤波器优化设计
2014-11-20吴秀山郇昌红
吕 威,吴秀山,胡 明,郇昌红
(中国计量学院机电工程学院,浙江杭州310018)
自从20世纪80年代可编程逻辑门阵列(FPGA)被发明以来,它被广泛地用作设计中等符合逻辑和不太复杂的状态机设计,且只能用在数据处理非常有限的的任务中。随着FPGA的容量、性能、运行速度等指标的提高,FPGA可以被用在越来越高端的应用中,例如在需要并行处理数据和对速度要求很高的系统中,由于基于FPGA系统的并行性,其处理速度往往快于在通用处理器上的软件实现。FPGA现在已经被普遍的应用在数字信号处理系统中。同时FPGA具有的在系统可编程的特性使得基于FPGA的设计成为在线可编程系统。FPGA也被用在了以前只能使用专用集成电路(ASIC)和微处理器才能实现的应用中,因为它可以提供相同的性能、低功耗、更短的研发周期和较低的开发成本[1-4]。
在一个用于脉冲宽度调制(PWM)的数模转换器(ADC)中,该系统的数字部分可以比较经济地在ALTER公司的AFlex10K器件上实现,使用这个装置可以迅速地对有功功率、无功功率和视在功率进行测量。这个功率分析仪在FPGA上实现,可以对单相功率进行测量,所占用的资源大概为该器件上60%的逻辑单元。所有的操作都是并行执行的,所以响应的时间非常短。为了得到正确的测量值,所有的信号必须先通过一个有限脉冲响应滤波器(FIR)。在硬件上FIR滤波器比无限脉冲响滤波器(IIR)更容易实现,这是因为FIR滤波器具有更简单和规则的结构,但是要达到相同的滤波效果,FIR滤波器往往比IIR滤波器具有更高的阶数,所以需要占用更多的硬件资源,所以在FPGA上实现FIR滤波器需要考虑速度、面积和功耗等约束条件,这就是为什么会提出一种不含乘法器模块的 FIR 滤波器的原因[1,5-6]。
1 FIR滤波器
具有固定系数的FIR滤波器是线性时不变数字滤波器,突出特点是其单位取样响应h(n)是一个N点长的有限序列,0≤n≤N-1,滤波器的输出y(n)可以表示为输入x(n)和单位响应f(n)的线性卷积

对于线性时不变系统,Z变换可以更方便地表示为

式中:F(z)为系统的传递函数,其表达式为

L阶线性时不变FIR滤波器可以用图1表示,实现1个数字滤波器需要的运算单元有加法器、乘法器和延迟单元等。乘法器为固定系数乘法器,该系数被称作阶权,历史上FIR滤波器也被称作横向滤波器,是由于它的抽头延迟线结构[7-9]。
数字信号处理的实质是数值运算,这些运算可以在计算机上用软件实现,也可以通过硬件实现。无论哪种方式,运算过程中的一些系数、信号序列及结果都要以二进制形式存储在有限字长的单元中。为了在FPGA器件中实现FIR滤波器,需要对乘法器的系数进行量化,如果乘法器的系数为整数的二次幂,或者是可以用两项或者三项二次幂表示,那么乘法器可以用移位寄存器替换。由于以前基于两项二次幂之和的系数替换误差较大,扩展到三项二次幂之和,并且计算了误差。图2为用加法器和移位寄存器替换的乘法器结构,乘法器的系数可以表示为

图1 直接型FIR滤波器

式中:ai,k范围是{-1,1};bi,k范围是 {-t,…,0,…,u},t和u决定了系数的动态范围,t和u越大近似值越接近于真实值[5]。

图2 系数为二次幂之和的运算单元
2 系数计算
滤波器的系数计算通过ALTERA公司的软件FIR编辑器或者其他专用软件来获得,一旦得到了该系数就可以将这些系数进行二次幂之和转换。
提出的转换系数的算法如图3所示,该算法将滤波器中乘法器的系数转换成二次幂的三项之和,如果将算法中的条件(i>2)替换成(i>1),则该算法可以很方便地将系数转换成二次幂的两项之和。
流程图中,a[i,k]和b[i,k]分别表示的是式(4)中的系数ai,k和bi,k,该算法有2 个循环结构,i循环计算的是向量a[i,k]和b[i,k],k循环用来计算滤波器中每个乘法器的系数。该算法的主要思想是计算系数f[k]的基于2的对数,在输入口的f[k]为乘法器的系数值。在第一步中,计算取决于系数的b[0,k]的二次幂的差,a[i,k]的取值-1或者1由有符号数f[k]除以f[k]的绝对值得到。
随着i值的增大,剩余的系数a[i,k]和b[i,k]相继被计算出。如果在某个节点或者是输入点,b[i,k]等于乘法器系数的字长n,滤波器的乘法相当于乘以系数0,因为此时滤波器的阶数为0。滤波器也相当于进行n位移位运算,在这个运算中,移位的方向并不重要,因为不管左移还是右移计算的结果都为0。当i>2时,此时k的值增加,下一个乘法器的的系数将被进行近似转换,由于在FPGA上实现该算法的复杂性,这些系数的转换将完全在外部进行,并且将计算得到的结果在FPGA的随机存储器上配置。

图3 乘法器系数的转换算法
3 测试结果
基于以上提出的系数近似转换算法,对比了二次幂的两项和三项和对乘法器系数转换误差的区别,图4描绘了在计算过程中将系数转换成二次幂的两项或者三项和的相对误差。可以看到,如果将一个字长为8位的系数用二次幂的两项之和来表示,那么相对误差最多可达10.3%,而用二次幂的三项之和来近似该系数时,相对误差将会低很多,最大误差为2.3%。如果乘法器系数字长为12位,用二次幂的两项之和的最大误差将达到10.8%,二次幂的三项之和的最大误差为2.6%。

图4 二次幂的两项和三项和近似误差(截图)
表1给出了几个整数系数的转换,可以看出将乘法器的系数用二次幂的三项之和来进行近似,精确度将远大于用二次幂的两项之和进行近似。

表1 系数转换的例子
在MATLAB软件上对以上提出的滤波器进行仿真,图5的结果是一个15阶的高通FIR滤波器的幅值响应,滤波器中乘法器的系数被量化到8位整数的精度,图中显示了系数量化前和系数近似为二次幂的两项或三项之和时的幅度响应,图中可以看出,将系数近似为二次幂两项之和后滤波器的阻带与系数量化前的阻带有很大的区别。
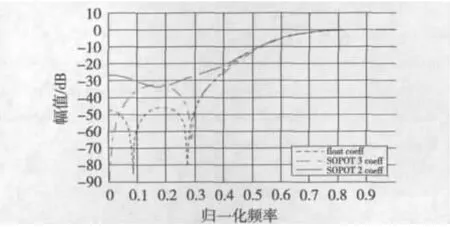
图5 三种不同系数编码的高通滤波器幅度响应(截图)
不过在有些情况下,将乘法器系数近似为二次幂的两项之和的滤波器可能在幅度响应上比系数近似为二次幂的三项之和更为准确,但是对于在FPGA上硬件资源的占用来说,将系数近似为二次幂的三项之和可以更加节约资源。
图6为一个13阶的低通FIR滤波器的幅度响应,可以看到只有在归一化频率为0.8~0.85时,将系数近似为两项二次幂之和的幅度响应比将系数近似为三项二次幂之和的幅度响应更为精确。
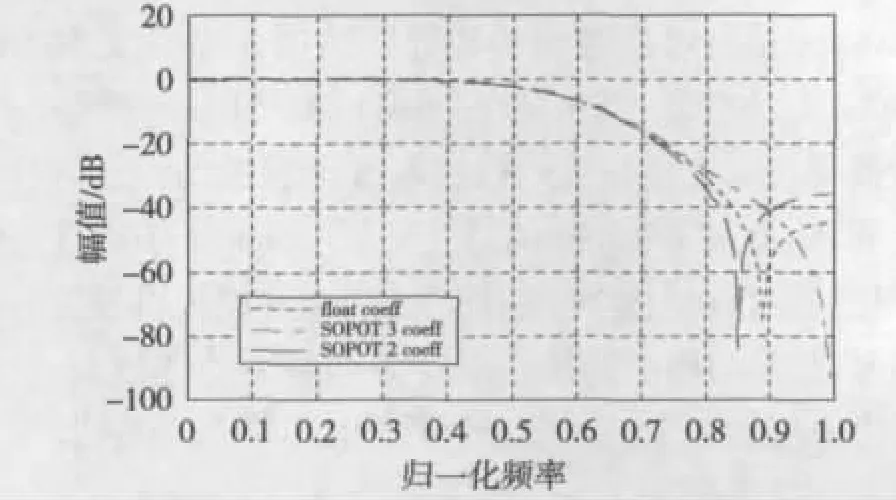
图6 三种不同系数编码的低通滤波器幅度响应(截图)
图7给出了基于三项二次幂之和系数的FIR滤波器框图,该结构很适合在FPGA上实现,只需做很小的修改就可以将其改变为系数近似为两项二次幂之和的滤波器结构。图中D表示为一个时钟周期延迟的单元,用D触发器实现。LSR是一个左移移位寄存器,由QUARTUS软件提供的参数化组合逻辑单元设计,该移位寄存器可以将输入左移3种不同的位数,由bi,k的数值决定。输入符号由的值确定,如果ai,k=+1,则输入符号为逻辑0,如果ai,k= -1,则输入符号为逻辑1,框图中的“+”代表加法器。
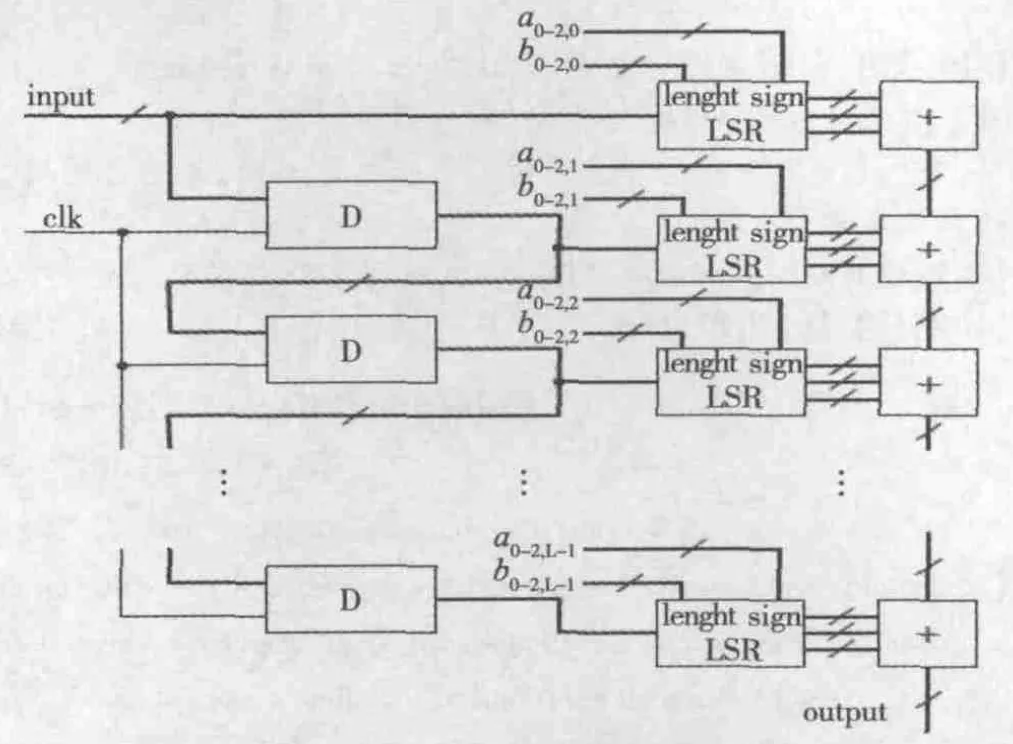
图7 基于二次幂三项之和系数的FIR滤波器框图
图7描述的结构在ALTERA的Flex10k器件中实现,一个7阶系数字长为12位的FIR滤波器用该方法实现,作为资源占用对比也用传统的含乘法器的结构实现该滤波器,传统的实现方法需要的逻辑单元为2 067个,而采用上述方法实现占用逻辑单元为1 540个。
4 结论
本文介绍了基于三项二次幂之和结构的FIR滤波器结构,采用该结构的滤波器与传统需要乘法器模块的滤波器结构相比,这种结构的滤波器具有很好的性能并且可以达到更快的速度,在FPGA器件上实现一个7阶系数为12位的FIR滤波器时,所占用的面积减小了近75%,这种新的结构可以让设计者在同一个FPGA器件上实现更多的滤波器。
[1]赵健等.数字信号处理[M].北京:清华大学出版社,2012.
[2]黄凤英.基于模块局部可重构FIR滤波器设计[J].电视技术,2013,37(9):83-86.
[3] PARHAMI B.Computer arithmetic:Algorithms and hardware designs[M].New York:Oxford Univ.Press,2000.
[4] CILETTID.Verilog HDL高级数字设计[M].张雅绮,李锵,译.北京:电子工业出版社,2005.
[5] PARHIK K.VLSI digital signal processing systems design and implementation[M].New York:Wiley InterScience,2003.
[6]金燕.FPGA应用中CIC抽取滤波器增益矫正的实现[J].电视技术,2013,37(7):57-59.
[7]高亚军.基于FPGA的数字信号处理[M].北京:电子工业出版社,2012.
[8] RABAEY JM,CHANDRAKASAN A,NIKOLIC B.数字集成电路——设计透视[M].2版.北京:清华大学出版社,2004.
[9]RABAEY JM.数字集成电路——系统与设计[M].周润德,译.北京:电子工业出版社,2004.
