一种基于压缩感知全变差算法的图像去噪方法
2014-11-20赵彦孟宋建新
赵彦孟,宋建新
(南京邮电大学图像处理与图像通信实验室,江苏南京210003)
1 图像去噪简介
图像是获取信息的一种重要媒介,但是当获取的图像中含有噪声时,获取的信息往往达不到人们的质量要求,因此,需要采用一种方法来去除图像中混有的噪声。随着信号处理技术的迅速发展,图像去噪也有了很大的改进。
传统的图像去噪方法有滤波器去噪方法和变换域去噪方法。滤波器去噪方法包括比较经典的均值滤波器法、高斯滤波器法、中值滤波器法和自适应最小均方误差滤波器法等。但是均值滤波器法和高斯滤波器法会在降噪过程中模糊图像的边缘信息。中值滤波器法虽然可以在图像去噪中保持尖锐的图像边缘信息,但会使图像的精细结构被抑制。自适应最小均方误差滤波器法虽然可以通过分析图像的局部强度统计信息,但是不能确保具有较高峰值信噪比(PSNR)的降噪图像获得可接受的视觉质量。变换域去噪方法主要是通过对含有噪声的图像进行变换,比如小波变换和离散小波变换等方法。基于小波变换的图像去噪方法证实在均方误差(MSE)和PSNR以及其他评估方法等方面优于传统的维纳滤波器法和中值滤波法等比较经典的去噪方法,但是如果噪声或者含噪图像的参数发生改变时,需要重新设计算法的参数,使算法的设计变得复杂。
本文在之前的研究基础上,运用一种新的图像去噪方法,将新兴的压缩感知方法应用到图像去噪中,消除了采用变换域进行图像去噪方法的问题。压缩感知方法将采样和压缩合二为一,改为对信息的直接测量,最后通过重建算法来实现图像的重建和噪声的去除。
当前的压缩感知重建算法主要包括凸优化算法和贪婪算法两大类。凸优化算法的思路主要是通过增加约束来取得最稀疏解,主要的重建算法有基追踪法(Basis Pursuit,BP)和全变差算法(Total Variation,TV)等。凸优化算法的计算量大,重建速度较慢,但是重建效果较好。贪婪算法的思路主要是根据匹配追踪(Matching Pursuit,MP)的思想,通过局部最优解依次找到各个非零系数,在此基础上出现了正交匹配追踪(Orthogonal Matching Pursuit,OMP),通过正交方向找寻非零系数,加快MP算法的收敛。典型的还有压缩采样MP(Compressed Sampling MP,CoSaMP)等算法。贪婪算法的重建速度较快,但是重建精度没有凸优化算法好。本文采用TV 重建算法作为图像去噪算法是因为其在去噪方面有较好的性能[7],TV算法是通过求解信号梯度而非信号稀疏解来重建信号。噪声的功率谱密度在所有频率上均为一常数,是一条平稳的直线,在变换域不具有稀疏性,但是噪声的梯度值具有稀疏性,这就促使本文通过采用TV算法来进行图像去噪。本文实验仿真中,对比了几种常用的压缩感知重建算法在图像去噪方面的性能。通过实验仿真证实,本文采用的压缩感知TV重建算法在图像去噪方面优于对比的压缩感知重建算法,可以实现图像的较好重建和噪声的有效去除。
2 压缩感知理论
传统的信号采集遵守香农奈奎斯特理论:为了实现无失真的信号重建,采样率需要大于等于信号带宽的2倍。但是由Candes和Donho等人提出的压缩感知理论[2-4]突破了这一局限,此理论证明稀疏或者可压缩信号可以从较少数量的线性测量高概率重建出原始信号,它要求测量矩阵和稀疏基矩阵之间满足不相干特性。
压缩感知理论要求信号具有稀疏性或者可压缩性,信号稀疏性是指信号X=[x(1),x(2),…,x(N)]T在标准正交基 Ψ = [ψ1,ψ2,…,ψN]上的投影 s= [s(1),s(2),…,s(N)]T中只有K个系数不为零或其他系数呈指数下降的趋势,且K≪N,表示为

在信号具有稀疏性的条件下,对信号X=[x(1),x(2),…,x(N)]T进行测量,选用的测量矩阵为 ΦM×N,通过原始信号在测量矩阵中的投影可得测量向量y,表示为

将式(1)和式(2)整理得

生成的测量向量y是M×1维列向量,从测量向量重建原始信号X的过程是病态的,无法精确求解X。如果信号具有稀疏性,可通过重建算法实现由低维的测量向量y精确地重建原始信号X。压缩感知系统框架如图1所示。

图1 压缩感知系统框架
实现信号较好重建的算法有基追踪法[2]和贪婪算法[5-6]。使用最小l1方法来实现信号精确重建可以通过求解下面的线性规划来获得信号X的稀疏解s^,即

然后,信号X可以通过式(5)来获得精确重建

实现信号的精确重建中,一个很重要的要求是测量矩阵Φ和稀疏基矩阵Ψ要满足非相干性,同时测量矩阵Φ要满足受限等距特性。因此,稀疏基矩阵可以选用小波变换基矩阵和离散余弦变换基矩阵,测量矩阵可选用高斯随机矩阵[1]。
3 压缩感知图像去噪
3.1 图像去噪的基本原理
为了实现图像去噪,首先将混有噪声的图像X进行稀疏域变换

式中:z为加性噪声。然后对变换后稀疏系数向量s进行测量,即

需要通过测量向量y来实现图像X的重建和去噪,实现重建的一个重要前提是信号为稀疏的。图像绝大多数是稀疏的,但是噪声在常规域下是不稀疏的。通过压缩感知理论对噪声进行稀疏变换,然后对变换后的系数进行M维测量,使得多数噪声已经被去除,仅含有M维的噪声向量。如果M数值越小,将会有更多的噪声信息被去除。通过对测量的M维噪声向量进行重建,去除混有的少量噪声,同时可以精确重建具有稀疏性的图像,从而达到去除图像中混有的噪声。
这种基于压缩感知的图像去噪框架如图2所示。

图2 压缩感知图像去噪框架
这种基于压缩感知的图像去噪算法的步骤为:
1)对混有噪声的图像X做离散余弦变换(DCT变换),获得变换后的稀疏系数s,表示为(X+z)=Ψs。
2)设计M×N维测量矩阵Φ,该测量矩阵Φ与稀疏基矩阵Ψ是不相干的。然后,通过测量矩阵Φ实现对部分稀疏系数s的测量,获得测量向量y,表示为y=Φs。
3)由测量向量y通过TV重建算法恢复图像信号X^,去除图像信号X中混有的噪声。
3.2 图像去噪的TV重建算法
全变差TV算法中,定义n×n大小的图像数据,用U表示,i和j表示图像的行与列坐标,从而可以用Uij表示其坐标点的像素值,则图像的水平与垂直一阶算子可表示为
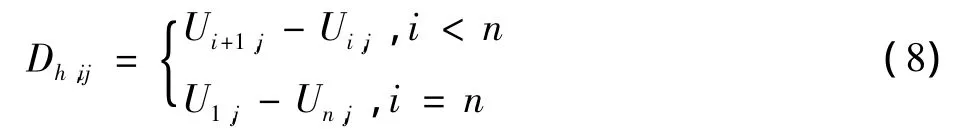

由于TV算法是以梯度算法为基础,图像中导数可以用相邻像素的差值表示,需要求出在水平方向与竖直方向的导数,以此两个方向的导数就可以确定图像变化的最快速变化方向,可以取最快速变化的反方向作为梯度的搜索方向,从而可以最快的速度逼近原始图像,恢复出原始图像。
离散梯度向量表示为

由式(8)~式(10)与全变差的定义,易得出其全变差值即为所有的像素离散梯度向量模之和,即

在算法迭代过程中可以以全变差的值作为迭代阈值,当在低于阈值时,就认为是重构出原始图像,但在重构的过程中允许误差的存在,当在误差允许范围之内时,则可以认为结果是正确的。
在式(8)与式(9)中定义了二维信号中梯度的表示方法,本文所用的算法是基于梯度的“TV”重构算法,二维图像信号每个像素进行简单的微分处理可得到总变差的每个像素的梯度,即

4 实验结果和分析
4.1 实验说明
首先,对混有均值为0、方差为0.01的加性高斯白噪声的图像进行DCT变换,然后,用高斯随机测量矩阵对变换后的部分系数进行测量,获得测量值向量。最后,通过上述的TV重建算法进行图像重建和噪声有效去除。
对混有加性高斯白噪声的原始图像进行DCT变换来获得稀疏化,保留DCT变换后的一部分系数(如10%或者15%),然后剩余系数置0。因为仅仅保留图像变换后的一部分系数,所以图像产生了失真,当保留的变换系数越少时这种失真越大,但是噪声的去除效果越明显。
4.2 实验一:TV算法重建图像
选取Lena.bmp图像作为原始图像,在原始图像中加入均值为0、方差为0.01的加性高斯白噪声,对混有噪声的图像进行DCT变换,保持DCT系数的前15%系数不变,剩余系数置0。对处理后的DCT系数选用测量矩阵进行测量,最后通过本文的TV重建算法来重建图像,仿真结果如图3所示。

图3 对混有噪声的图像进行稀疏度为15%的重建图像
图3a是原始图像;图3b是加入均值为0,方差为0.01的加性高斯白噪声图像;图3c是对图3b进行稀疏化为15%的重建图像;图3d是对图3c采用TV算法重建后的图像,采样率为22.80%。
比较图3b和图3d中的PSNR可知,在采样率可以保持较低值22.80%时,运用压缩感知方法的全变差重建算法可以有效地去除图像中混有的噪声。
在上面实验的基础之上,使图像的稀疏度变为10%,用测量矩阵对混有加性高斯白噪声的稀疏度为10%的图像进行测量,最后通过TV重建算法来重建图像,仿真结果如图4所示。
图4a是原始图像;图4b是加入均值为0、方差为0.01的加性高斯白噪声图像;图4c是对图4b进行稀疏化为10%的重建图像;图4d是对图4c采用TV算法重建后的图像,采样率为15.67%。
比较图4b和图4d中的PSNR可知,在采样率可以保持在较低值15.67%时,运用压缩感知方法的全变差重建算法可以有效去除图像中混有的噪声。
通过实验一中的仿真,可以看到运用压缩感知方法中的全变差重建算法进行图像去噪,能够很好地去除图像中混有的噪声。比较图3c和图4c中PSNR可知,虽然稀疏度值越小图像去噪越明显,但是图像的重建效果却变差。这是因为稀疏度值越小,原始图像的信息丢失也会越多,所以在重建图像质量上可以根据图像去噪和原始信息的丢失进行权衡。
4.3 实验二:TV算法和其他算法比较
选用Baboon.bmp图像作为原始图像,在保证混有加性高斯白噪声图像的稀疏度不变的条件下,通过增加测量值M的个数,来研究重建图像的PSNR随采样率的变化关系。仿真结果如图5所示。
在上面实验的基础之上,通过仿真刻画了“PSNR随采样率的变化曲线”。并将本文的TV算法与压缩感知的其他重建算法如正交匹配追踪(OMP)算法和压缩采样匹配追踪(CoSaMP)算法进行对比。该曲线显示,随着测量值个数M的逐渐增加,本文TV算法重建性能优于对比算法。并且重建图像的PSNR获得一种近似线性提升。仿真结果如图6所示。
通过实验二中的仿真,保证稀疏度不变的条件下,通过增加对图像测量值的个数,使得重建图像的质量获得较大改善。这是因为测量值的个数越多,对图像的测量越准确,使得重建时对图像的重建效果越好。
5 小结和研究展望
本文描述和仿真了一种基于压缩感知的图像去噪方法。首先将混有白噪声的图像进行离散余弦变换,然后对变换后的一部分系数进行保留,将剩余的系数进行置0。通过对保留的系数用傅里叶变换域的射线采样模式作为测量矩阵进行测量,最后通过引入TV重建算法实现了图像恢复和噪声去除。仿真证实该方法明显改善了图像去噪的性能。本文采用一种新的压缩感知TV重建算法,在图像去噪方面优于对比的压缩感知重建算法,可以实现图像的较好重建和噪声的有效去除。
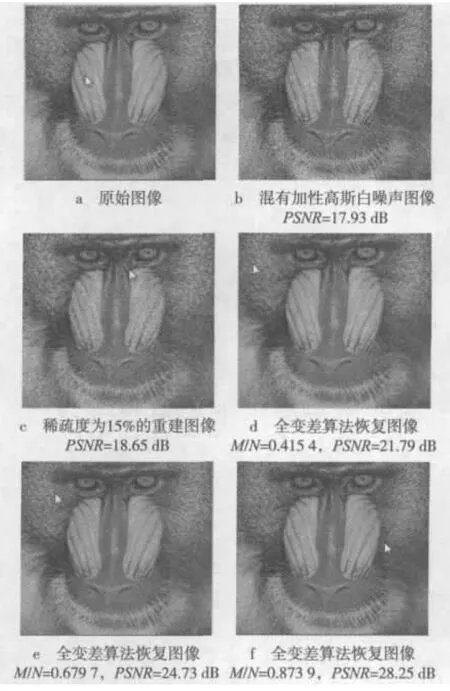
图5 重建图像的PSNR随采样率变化关系

图6 PSNR随采样率的变化曲线
在无线环境下如果测量值向量在传输过程中混有了噪声,如何处理该问题将是接下来的研究重心。
[1] DONOHOD.Compressed sensing[J].IEEE Trans.Information Theory,2006,51(4):1289-1306.
[2] CANDESE,ROMBERG J,TAO T.Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information[J].IEEE Trans.Information Theory,2006,52(2):489-509.
[3] CANDESE.Compressive sampling[J].Int.Congress of Mathematics,2006(3):1433-1452.
[4] BARANIUK R.Compressive sensing[J].IEEE Signal Processing Magazine,2007,24(4):118-124.
[5] CANDESE,TAO T.Decoding by linear programming[J].IEEE Trans.Information Theory,2005,51(12):4203-4215.
[6] DAVISG,MALLAT S,AVELLANEDA M.Greedy adaptive approximation[J].Constr.Approx,1997(13):57-98.
[7] BUADESA,COLL B,MOREL J.A non-local algorithm for image denoising[C]//Proc.CVPR 2005.[S.l.]:IEEE Press,2005:60-65.
[8] LUSTIGM,DONOHOD,PAULY J.SparseMRI:The application of compressed sensing for rapid MR imaging[J].Magnetic Resonance in Medicine,2007,58(6):1182-1195.
[9]石光明,刘丹华,高大化,等.压缩感知理论及其研究进展[J].电子学报,2009,37(5):1070-1081.
[10] ZHU L,ZHU Y,MAO H,et al.A new method for sparse signal denoising based on compressed sensing[C]//Proc.KAM ’09.Wuhan:IEEE Press,2009:35-38.
