朱载堉等程律创立流程探析——几何、算术、音律与物理声学的综合

刘娅娅

(西北大学数学学院数学与科学史研究中心，西安710127)

等程律无疑是古代中国对世界文明做出的伟大贡献，其发明者朱载堉(1536～1611)“潜思有年，用力既久”，［1］在充分汲取前人经验教训的基础上，首发“新法密率”，即十二等程律(12-tone equal temperament)，彻底解决了几千年来律学史上的“返宫”①中国古代“返宫”概念对应西方的“closed cycle”，指八度圈是否为一个封闭的圆。难题，这是他在声学、律学、算学和文化史上获得的最伟大的成就［2］。鉴于朱载堉等程律的重要性，中外诸多学者对此都有所研究，但由于语言、文献等方面的障碍，一些西方学者对朱载堉等程律的创立或持怀疑态度，如美国学者库特纳(Fritz A.Kuttner，1903～1991)曾提出:“朱载堉没有对等程律作出数学或理论的解说，只给出了部分的演算程序。”［3］近代，随着学者们对朱载堉著作的译注、传播及算法的复原，这种质疑已逐渐灭迹，但对朱载堉首发十二等程律数学计算和理论框架的复原研究还有待完备与深化。本文在对朱载堉等程律创立流程的复原过程中发现，其等程律创立的代表作《律学新说》(1584年)、《律吕精义》(1596年)及《算学新说》(1603年)中所述新法密率的创立流程体现出了高度的数值分析思维，如将朱载堉自制八十一档大算盘②朱载堉独创八十一档大算盘，计算精度达到二十五位。比作现代计算机，这种对应将更加突出的显现出来。

1 律学上的难题——实际问题的提出

1.1 律学上的实际问题

历代律学家在律制探索的道路上，逐渐认识到三分损益法不能实现“黄钟还原”，①“黄钟还原”与“返宫”目的一致，从第一律黄钟出发经过某种计算再回到出发律，三分损益法不能实现“黄钟还原”的根本原因就是其相生因子2/3，4/3计算所产生的最大音差。针对这一问题，朱载堉在《律吕精义·序》中说到:

臣尝闻臣父曰:“六经有听律之文，无算律之说，律由声制，非由度出。黄钟之声既定，则何必拘九寸?执守九寸，为说误矣……则知三分损益之法非精义也。”臣闻此语，潜思有年，用力既久，豁然遂悟:不用三分损益之法，其义益精。(［1］，27页)朱载堉已认识到黄钟还原问题是律学史上的一大未克难题，且其产生的原因有:(1)律音是由测音器所产生的声调高低(取决于发声体振动的频率f，朱载堉时期虽无频率及音程概念，但已通过管、弦等声学试验，掌握以弦长或管长数据计算律长以定各律音高之法，遵循λ=1/f)所定，而非由度量标准产生，这是律学的物理本质。(2)黄钟音高确定，为何拘守九寸，固守九寸为黄钟的说法是一种误解。②《律吕精义·不宗黄钟九寸第二》曰“黄钟(之声高)无所改，而尺有所不同”。(3)三分损益法计算精度不足。

1.2 历代造律的弊端及矫正要点

旧律不能实现黄钟还原，有其内在原因，朱载堉指出历代造律之三弊端:(1)“王莽伪作非至善”，王莽度制本身存在问题③《汉书·王莽传》曰:清丽而哀，非国之声也。朱载堉评:根本不正，此之谓也。;(2)“刘歆伪辞全无可取”，刘歆考据不明，不可取用;［4］(3)“三分损益旧率疏舛”，三分损益旧率计算粗疏舛错。矫正旧律有三个要点:“不宗王莽律度量衡之制，一也。”不依据王莽所定度量衡制;“不从汉志刘歆班固之说，二也。”不依照刘歆、班固的理论;“不用三分损益疏舛之法，三也。”不用粗疏舛错的三分损益法。(［1］，1页)这里需指出，三分损益律虽不得还原黄钟，但其以纯五度生律，保证了各律音调的纯正。［5］

1.3 两个实例——京房六十律与何承天新律

在朱载堉创立新法密率之前运用三分损益法解决黄钟还原问题上，有代表性的两种律算有——京房六十律与何承天新律。汉京房(公元前77～前37)在三分损益法生律越多越有可能回到黄钟律的指导思想下，其所制六十律仍未能在理论上解决黄钟还原问题④南朝宋元嘉太史钱乐之更是在京房六十律基础上依三分损益法计算到了三百六十律。。朱载堉引《宋书·律历志》评论到:“‘京房⑤西汉律学家，本姓李，字君明，提出“竹声不可度调”。不思此意，引而伸之，仲吕上生执始，执始下生去灭，至于南事，为六十律，竟复不合，弥益其疏。’［6］算术不精，此之谓也。”(［1］，2页)事实上，京房六十律仍属三分损益律范畴，具体计算法是:“是故十二律得十七万七千一百四十七，是为黄钟之实。又以二乘而三约之，是为下生林钟之实……推此上下，以定六十律之实。”［7］

京房先设黄钟律数177 147、黄钟律长9寸、京房准黄钟长9尺。依三分损益法计算，由第十二律仲吕再上生一律到第十三律执始［共计上生7次(4/3)7，下生5次(2/3)5］，并未回到出发律黄钟。按照英国语言学家、比较音乐学家埃利斯(Alexander John Ellis，1814～1890)所创音分值计算法①音分的发明者，定义音高的物理声学原理，八度音程频率比2:1分成均等的1200份，对应数值为所求音分值，用对数表示音程关系:xn/log(fn/f0)=1200/log2。，可知是由执始律f12与黄钟律f0的音高差所导致:

将(1)式代入(2)式，计算执始与黄钟音差的音分值:

这个音差称为最大音差或古代音差。为消除这个音差，即实现黄钟还原，从汉代开始律学家们做出了艰辛努力，这也成为推动古代律学发展的内在动力。在执始律宣告失败后，京房继续向下计算，一直计算到第六十律南事律。事实上，不必计算到60律，当京房生律53次计算到第54律时，得到了比执始律更接近黄钟的色育律:

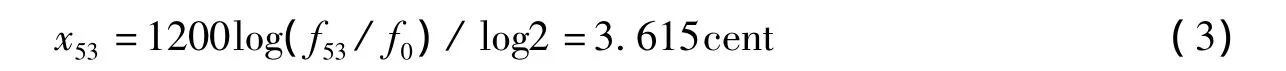
这个音分值与黄钟只有3.61音分之差，已达到了六十律内与黄钟律最小差值，现称为京房音差。尽管理论上，京房音差使古代音差大大缩小，人耳难于辨别，但就乐器制造与演奏实践而言，其本来就不具有实用价值。［8］

相对于计算更多律的做法，另一批律学家的做法是仍保持十二律，只在各律之间做出相应调整，使之达到黄钟还原与旋宫转调的要求。这方面比较有代表性的是南北朝何承天(370～447)，他精于律学与历法，反对京房一味增加律数的做法，而仅在十二律内部调整各律的高度，使仲吕上生得黄钟，从而实现黄钟还原。《隋书·律历志》援引何承天的话说:“上下相生，三分损益其一，盖是古人简易之法。……后人改制，皆不同焉。而京房不悟，谬为六十。”因此他才“更设新率，则从仲吕还得黄钟，十二旋宫，声韵无失。”［9］

何承天依三分损益法衍生新律，从黄钟9寸生律十一次得仲吕，再上生一次:6.66×=8.88寸并不能回到出发律黄钟9.00寸，与黄钟差值:9.00-8.88=0.12寸。何承天的解决办法是将这个差数0.12均分为首项0.00，末项0.12，公差0.12/12=0.01的13项等差数列，依十二律五度相生次序分别加在各律之上②并非依据各律长短次序。，最终使得仲吕上生一次8.88+0.12=9.00可回到出发律黄钟，且与三分损益法所生各律差数不致过大，其效果非常接近等程律，一般人的听觉几乎不能辨别二者的差别。［10］具体计算程序如表1所示。

表1 何承天新律与等程律音分值比较1)

续表1

何承天新律尽管在形式上实现了黄钟还原，且效果上十分接近等程律，但仍未真正实现旋宫转调，因其人为设定的黄钟、清黄钟八度关系是不稳定的，倍、正、半黄钟间的计算仍未实现统一。朱载堉通过总结前人经验教训，认识到在十二律之外增加新律无论是在律数计算还是音乐实践上都是行不通的;而依三分损益计算再“适当”调整音律的做法只能在形式上实现“黄钟还原”。真正的黄钟还原不仅要满足听觉上的需求，更要在“数”上达到新的精度，使得倍、正、半律之间实现计算统一、旋宫转调的自由切换，这必须突破三分损益律框架，新律的探索势在必行。

2 律与度量衡——创立数学模型

音乐学可分为两大类:一类分析音乐如何作成，找出其中可成为标准的要素，这便是音乐理论;二类是分析音乐如何作成时，所发现标准的“成立理由”。［11］律学显然是属于后者音乐科学范畴，它从发声体的振动规律出发，运用数理计算研究乐音高低关系，又称为数理音响学。［12］中国古代五声、七音、十二律至迟在周朝已进化成立，各律构成音阶的每个音，在高度上有精密的规定(表2)。三分损益律和纯律都通过“以耳齐声”①最早见于东汉蔡邕(133～192)《月令·章句》:“古之为钟律者，以耳齐其声，后人不能，则假数以正其度。”这种最原始的方法找到了几个自然音程，其具有音调谐和优势，但黄钟还原问题仍困扰着历代律学家，对传统谐和律音的取舍也显得异常困难。［13］如何为新律扫除障碍成为当务之急，《律学新说·律吕本源第一》提出解决律吕问题必始于精密数学计算:

夫河图、洛书者，律历之本源，数学之鼻祖也。……易曰:“河出图，洛出书。圣人则之。”所谓则之者，非止画卦、叙畴二事而已，至于律历之类无不皆然。……河图之数五十五，视大衍而有余;洛书之数四十五，视大衍而不足。合河图与洛书共得百数，……均而分之，得大衍之数者二。此天地自然之至理，故律历倚之而起数。［14］

朱载堉认为河图、洛书是律历之本源，数学之鼻祖，与“律历之数乃天地之道”相印，［15］是他对上古经典的高度肯定，同时亦表明他充分认识到数学计算在律学研究中的重要性。其后，《律吕精义·序》界定律学研究中“声”与“数”的辩证关系:

殊不知律历之学以声数为至要，若夫辩论乃其末节也。声者，合四一上勾尺工凡六五之类是也;数者，一二三四五六七八九十之类是也。前贤多不留心于此，……故于论数目尺寸、声调腔谱处，率删去之，此则史家之通弊也。夫乐也者，声音之学也;律也者，数度之学也。欲志乐律，宜详其本。(［1］，3页)

“声”与“律”的概念和职能:

表2 中国古代音与律关系表［16］

面对三分损益法不可撼摇的地位，朱载堉通过敏锐的观察和实验，强调律学研究“声”与“数”之重要性:黄钟的标准音高或绝对音高决定黄钟律长取值;数学方法不同，可能产生不同的律制。《律吕精义·不宗黄钟九寸第二》将“律”与“度”的关系概括为:“律由声制，非由度出，制律之初，未有度也;黄钟无所改，而尺有不同。”(［1］，3、6页)“律”先于“度”存在;黄钟律的绝对音高是不变的，而度尺随各朝代更替变化。对“律”与“度”关系的正确认识，促使朱载堉摒弃了宗守黄钟九寸做法，而是按照标准起始音(由黄钟音高而定)选取利于计算的律长，使得新律创立伊始既遵循声学原理，又克服了度尺标准不同所造成的阻碍。

朱载堉凭借在律学和算学方面的深刻钻研，认为欲实现黄钟还原必借助更精密的计算，将实际问题转化到数理模型中，从而突破以往仅依赖听觉感知及拘守三分损益法的局限，创造出新的更加精密的律制。［17］他探究旧法弊端，厘清“声”、“数”、“律”、“度”关系，《律学新说》与《律吕精义》首发“新法密率”的数学模型:

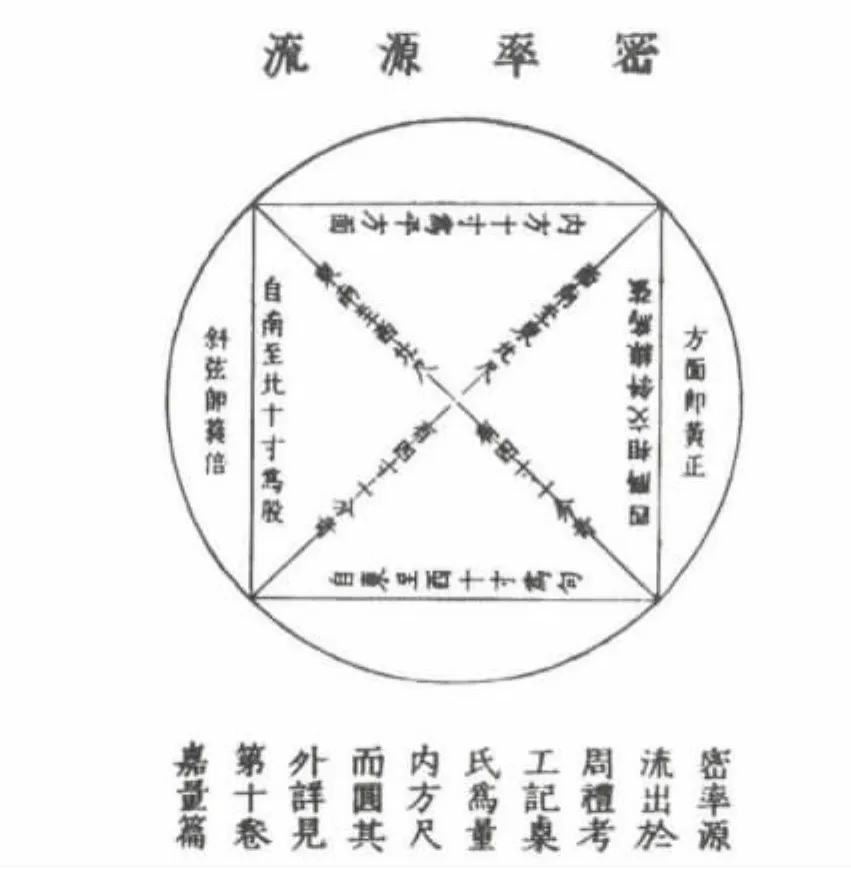
图1 密率源流图

3 朱载堉新法密率之计算程序

下面这段取自《律吕精义·不用三分损益第三》的文字历次被援引最多，介绍新法密率之计算程序:

(1)度本起于黄钟之长:“度本起于黄钟之长，则黄钟之长即度法一尺。命平方一尺为黄钟之率。”(［1］，9页)度量长度的标准尺起源于黄钟律的长度，因此黄钟正律之长就是标准尺一尺，令平方一尺作黄钟之率:

黄钟之长=1尺 黄钟之率=1尺·1尺=(1尺)2=(10寸)2=100寸2(2)蕤宾倍率的释义:“东西十寸为句，自乘得百寸为句幂;南北十寸为股，自乘得百寸为股幂;相并共得二百寸为弦幂。乃置弦幂为实，开平方法除之，得弦一尺四寸一分四厘二毫一丝三忽五微六纤二三七三〇九五〇四八八〇一六八九为方之斜，即圆之径，亦即蕤宾倍律之率。”(［1］，9页)定义黄钟正率后，设计出句股弦幂模型，并据此计算出蕤宾倍率精确数值①精确到小数点后二十四位。。蕤宾倍律是黄钟正律到黄钟倍律这十三律的中间一律，也是计算新法密率的关键，探析蕤宾倍率计算，是复原新法密率创立流程的关键:

(a)句幂、股幂与弦幂:

句=10寸(东西)句幂=10寸·10寸=100寸2(句方面积)

股=10寸(南北)股幂=10寸·10寸=100寸2(股方面积)朱载堉在从黄钟正率数值出发，做句、股、弦幂模型:

句幂=股幂=黄钟正率=1尺·1尺=10寸·10寸=100寸2(黄正方面)

弦幂=句幂+股幂=100寸2+100寸2=200寸2=2·黄钟正率 (弦方面)

句+股=10寸+10寸=20寸=2·黄钟律长

(b)密率源流与句股弦幂

依密率源流图“内方外圆”与句股弦幂模型，将黄钟正率方面平移到句股弦方内，再做黄钟正率外接圆，构造密率源流-句股弦幂图，此圆恰为弦方内切圆。“方之斜、圆之径”即“密率源流”的“斜弦”:在密率源流-句股弦幂图中位于黄正方面与二倍黄钟正率弦幂的正中间;数值上句股求弦得，黄钟正率为1，二倍黄钟正率弦幂为弦自乘成黄钟正率与二倍黄钟正率之等比中项，为十三个率的最中间一率，即蕤宾倍率。将“密率源流图”方圆相函模型与(1)、(2)所述相对应并建立“圆之径、方之斜”蕤宾倍率计算模型，如图2所示。

图2 密率源流与句股弦幂求解蕤宾倍率示意图

(c)蕤宾倍率求解

参照“内方外圆”与句股求弦模型而构建的“弦幂①句股之弦为边长的弦方面积。-圆-方面”模型，使得蕤宾倍率的求解具备了合理性。“ 氏为量”与上文求解蕤宾倍率中反复提到“圆径与方斜同”:“圆之径、方之斜”是蕤宾倍率的几何意义;句股弦则是它的算法，是求解“圆之径”的途径，借助于句股与开方术，即可求得“圆之径”精确数值，比直接求解“圆之径”要简便许多。《不用三分损益法第三》给出“圆之径”的解法:“乃置弦幂为实，开平方法除之”:

对蕤宾倍率求解几何模型与文中计算出的数据进行整理分析，列为表3。

图3 黄钟正律-蕤宾倍律-黄钟倍律递推图

表3 蕤宾倍率计算递推表

图4 密率周径与密率源流图

《律吕精义内篇卷二·不取围径皆同第五之上》①密率源流、密率周径对比图见于《律吕精义内篇卷二·不取围径皆同第五之上》。又将新律广推到管律，探讨各律围径问题:“旧律围径皆同，而新律各不同;先儒以为，长短虽异，围径皆同此未达之论也。”(［1］，41页)朱载堉修正先儒管律之法，将计算新律的“密率源流”思想及结果推广到管律计算，所取各律既长短互异，又围径皆不同，篇首相并给出“密率周径”与“密率源流”图:“外周用弦求句股术得其内周，内径用句股求弦得其外径”;“外周内容之方即内径也，内周外射之斜，即外径也。”(［1］，42页)律管内周(之弦)与外周(之弦)是勾股求弦(反之则为弦求勾股)的关系，对应黄钟倍率、蕤宾倍率黄钟正率间的递推关系:

黄钟倍率(弦幂):蕤宾倍率(斜弦)=蕤宾倍率(斜弦):黄钟正率(方面)黄钟倍律(斜之斜):蕤宾倍律(方之斜)=蕤宾倍律(方之斜):黄钟正率(方边)

蕤宾倍率是黄钟倍率与黄钟正率正中一率，在密率源流与密率周径几何图中，蕤宾倍率(方之斜、圆之径、弦方边)亦位于二者正中，这无疑是朱载堉绝顶聪明的首发之举，它使得黄钟还原最关键一步迈出了:计算出蕤宾倍率，确定黄钟倍率、蕤宾倍率、黄钟正率这三率成首项2，末项1，中项，公比等比排列。这足以否定对朱载堉新法密率的不合理评价:“借勾股之名以欺人耳;错误搬用《周礼·氏为量》经典记载作为合法外衣。”［19］

其余十律的计算就转化为等比数列求解问题，在此篇末朱载堉以历法冬夏二至、春秋二分为喻，引出夹钟、南吕倍率求解过程:“造率始于黄钟，必先求蕤宾者，犹冬夏二至也;次求夹钟及南吕者，犹春秋二分也。始于黄钟者，履端于始也;中于蕤宾者，举正于中也;终于应钟者，归余于终也:律与历一道也。”(［1］，15页)以“春秋二分”比夹钟、南吕倍率分布在黄钟(倍、正)与蕤宾倍率“冬夏二至”正中，南吕倍率:“以句十寸乘之，得平方积一百四十一寸……为实，开平方法除之，得一尺一寸……即南吕倍律之率。”(［1］，9～10页)南吕倍率是蕤宾倍率与黄钟正率的等比中项，以句十寸(黄钟正律)乘蕤宾倍率积算开方:

=1.1892071150027210667175尺

(3)应钟倍率为密率

应钟倍率居南吕、无射、应钟倍率，黄钟正率四项等比数列第三项②朱载堉在《乐律全书》最后雕版完成的《算学新说》(1603年)第七问中介绍了四项等比数列求解方法。，仍做立方积开立方:“仍以句十寸乘之，右以股十寸乘之，得立方积一千一百八十九寸二百〇七分一百一十五厘……为实，开立方法除之，得一尺〇五分九厘四毫六丝三忽〇九纤……即应钟倍律之率。”(［1］，10页)至此，黄钟还原问题宣告解决:

通过上述复原分析特别是对蕤宾倍率的释义，作为等程律计算的关键，半音音比应钟倍率计算的这三个步骤得来何其不易，况且《律吕精义》在给出这套程序之前，朱载堉仅在《律学新说》中已做出了大量准备工作。所谓三步说，只是站在结果的角度，过分强调了数学计算本身，殊不知律学绝不能脱离它的物理声学及乐理实践而单独存在，在这里困难的是如何舍弃五度谐和音程而不用、如何舍弃等差计算而不用、如何以蕤宾倍率为突破等，这无疑是经过一系列漫长思考、钻研后高度提炼的结果。对于这种片面评价，朱载堉似乎有所预知，他在《律学新说》开篇感叹:“慨生之既晚，不获与前辈同游，虽有一得之愚，无凭质问。楚辞有云:‘往者余弗及，来者吾不闻。’亦可悲哉!聊述愚见数篇，刻而传之，以俟方来具眼之士，或有可取焉。”(［14］，9页)

新法密率是朱载堉通过将律与度量衡及天文、历法、算术、几何、音乐、声学等研究结合起来的突破性成果，是一个递进性的大型综合研究，决非否定等差数列，自然过渡到等比数列的简单推论。他据周礼量器“内方圆外”图形中方边与圆径的关系，作其密率源流，渊源于中国古代“以器载道”的思想及“同律度量衡”制度，“内方尺而圆其外”既是借助于周鬴、嘉量标准法器以古寓新，又是古代律学与数学共同面临的问题;用句股术创制新法，一举解决了黄钟还原这一律学难题，又使得等程律遵循了物理声学的基本法则。(［5］，155页)

4 朱载堉新法密率之计算方法

结合上文中新法密率求解所需的数学方法:勾股求弦术、开平方、四项等比数列求解问题、开立方法等。中国古代数学经典《九章算术》即涉及了有关的计算方法，从宋代开始，贾宪(11世纪)、秦九韶、朱世杰(13世纪)已完成了开平方、开立方和以增乘开方求高次方根的简便方法。直接求高次方根的简便方法在14世纪初年以后失传了，因此朱载堉所用的仍是《九章算术》中“置积为实”的开方术，即先求平方积或立方积、再求平方根或立方根的方法解方根的数学方法。数列求解等问题早在汉《周髀算经》中已有涉及，《九章算术》在粟米章、衰分章、均输章和句股章均有许多不同类型的比例求解问题。［20］

朱载堉本人对这些计算问题的解决在他的新说中亦有所体现:《律学新说》首发密率，篇首曰:“凡非数术音声之技，兹并不述，所谓各志其志而已。”(［14］，9页)言明其志在运用数学计算解决律学难题。《律吕精义·内篇》构建了计算密率的数学模型、演算程序并给出计算结果。《算学新说》①《算学新说》收于郑藩刻本《乐律全书》1603年成书，涉及珠算开平方、立方、等比数列求解等问题。梳理了密率计算所要涉及的数学方法:“臣所撰新说凡四种:一曰律学，二曰乐学，三曰算学，四曰韵学。前二者其书之本原，后二者其书之支脉，所以羽翼其书者也。”［21］朱载堉著述新说始终坚持以解决律学问题为本原，数学或算学方法成为新法密率创立的必要条件，系统阐述相关的计算方法是对新律理论的充实和扩充。对明朱载堉而言，迈出渊源已久的三分损益法，反复律管实验探求声学本质，寻求等比计算解决黄钟还原问题的可能性，以及对“声”、“数”、“律”、“度”关系的正确把握是探求新律之本原，求解密率所涉数学问题以“羽翼其书”二者缺一不可:

(1)应钟倍率算法释义

应钟倍率数值作为计算新法密率各律之“法”数值，这个计算几乎包含了完成新法密率所需的全部数学方法。结合上文流程分析，朱载堉在“新法密率”创立之初，利用弦长计算各律数值，认识到弦长与音高的关系:黄钟、蕤宾、南吕、到应钟这四律在八度内弦长递减、音高递增，各律成等比排列。《律学新说·密率律度相求第三》说道:“惟琴家安徽，其法四折去一，三折去一，俗工口传，莫知从来，疑古人遗法如此，特未记载于文字耳。”(［14］，18页)以琴家徵位结合以历法二至、二分点介绍了比例中项概念与应钟倍率的推演过程:“冬夏二至”比黄钟与蕤宾，蕤宾倍率26/12位八度音程212/12的一半处;“春秋二分”、“四折去一”比做夹钟29/12、南吕23/12，位八度音程的3/4、1/4处，即黄钟与蕤宾比例中项;南吕倍率“三折去一”即为应钟倍率21/12，其在南吕倍率、无射倍率、应钟倍率、黄钟正率这四律音程的1/3处，即为十二律的半音音程，亦即“公比数”。朱载堉在其著作中虽未提及“公比数”这个概念，事实上他已将此概念由黄钟、蕤宾、南吕再到应钟这样的步骤最终巧妙的定义出来了。

朱载堉《律吕精义》中计算“公比数”应钟倍率数值步骤与《算学新说·第七问》所载一致:“置南吕倍率以黄钟再乘，得立方积开立方所得，即应钟倍律也。”(［21］，12页)将这段用现代数学公式表示:

这表明计算应钟倍率涉及到四项等比级数求解与指数运算问题:设南吕倍率、无射倍率、应钟倍率、黄钟正率组成的四项等比级数:A，x，y，B。已知A，B，求:x，y。

由于黄钟正率取值1，这个打破历代黄钟9寸的做法，使得应钟倍率的数值在形式上表现为:

这就是导致朱载堉的等程律计算常被认为是只有简单三步的原因。但即就如此，在朱载堉所处的时代这也并非不证自明的公理，这涉及指数函数①黄钟倍率长2连续开方运算。借琴家徵位“四折去一，三折去一”来阐述他发现并验证指数运算定律。的性质问题，在当时是需要努力证明的:

在西方与朱载堉同时代的荷兰工程师、数学家西蒙·斯蒂芬(Simon Stevin，1548～1620)，在朱载堉之后一年出版了一本以法文书写的数学小册子L’arithmetique(《论算术》，1585年)，系统介绍了计算开平方与开立方的方法及1/2②斯蒂芬八度仍为弦长之比1:1/2=2:1，此处1/2的十二次方根是他的等程律的半音弦长。开12次方的算式，也就是上述指数函数得以成立的依据。［22］1606年，他完了的一份音乐理论手稿Vande Spiegheling Der Singconst(《论歌唱的艺术》)，他结合音乐理论与开方运算，计算出了十二律各律数值。［23］这份手稿直到1884年才在荷兰官吏、音乐家惠更斯(Constantijn Huygens，1596～1687)①荷兰物理学家、天文学家、数学家克里斯蒂安·惠更斯(Christiaan Huygens，1629～1695)的父亲。的收藏中被发现，至此它被遗忘了近300年后才终于公诸于世，这标志着斯蒂芬均等音比的音律系统的建立，这也成为等程律在欧洲真正诞生的标志。

(3)对密率应钟倍率的验证和应用

新法密率计算八度(弦长比为2:1)内十三个律成等比排列，且其公比为。朱载堉通篇所探讨的优于三分损益之“密率”，及《律学新说》、《律吕精义》中反复提到的:“是故不用三分损益之法，创立新法。置一尺为实，以密率除之凡十二遍，所求律吕真数，比古四种术尤简捷而精密”;(［14］，19页)“是故各律皆以黄钟正数十寸乘之为实，皆以应钟倍数十寸〇五分九厘四毫六丝三忽〇九纤……为法除之，即得其次律也。十二律黄钟为始，应钟为终，终而复始，循环无端。”(［1］，10页)“密率”应钟倍率作为“公比数”半音音程是实现黄钟还原、周而复始的唯一方法。［24］

5 朱载堉新法密率之全面推广

朱载堉创立新法密率，从黄钟正率出发，依据密率源流图几何直观计算出蕤宾倍率后，确定十二律成等比排列，按照蕤宾、南吕、应钟、黄钟四项等比级数求解法，最终得到公比应钟倍率即新法密率，据此可算出十二律全部数值:“是故各律皆以黄钟正数十寸乘之为实，皆以应钟倍数十寸〇五分九厘四毫六丝三忽〇九纤……为法除之，即得其次律也。是故新法不用三分损益，别造密率，其详如左(积算旁通图)。”(［1］，11～15页)积算旁通图从黄钟倍律积算二起算，又新造密律二种:以黄钟之率二十兆、黄钟之率十亿以密率除之，逐一求解各律律长。

令L表示长律，l表示短律，则长短相生表示如下:

若以x表示长生短系数，“隔八相生”黄钟生林钟为例，则有:

新法密率“隔八相生”系数x即为五度音程弦长比1/27/12①短生长，再降八度即2/27/12。，据此从黄钟出发计算到第十二律仲吕再按密率五度隔八生一律(短生长)到黄钟，实现黄钟还原。这显然优于三分损益旧法之“仲吕极不生”②《淮南子·天文训》卷三。。通过(2)式可以看出密率五度相生系数500 000 000/749 153 538，这显然是对五度音程弦长比1/27/12的一个近似展开，以便于各律间的相生计算。而之所以不直接运用1/27/12这个系数，与上文中有关指数函数性质情形类似，其计算过程仍是需要证明的③指数运算另一定律:ax/ay=ax-y。。需要指出的是，若此近似展开只近似到百万位其比值500/749就非常接近三分损益律的五度弦长比2:3(即500/750)，即钱德明(Jean Joseph Marie Amiot，1718～1793)的提出的中国古代“749”定律法④钱德明1780年出版中国律学著作中介绍过此方法，但未指明出处，被认为是近似等程律。。库特纳发现钱德明关于中国古代律学的著作在介绍这种调律法时并没有提出文献出处，但他通过查阅朱载堉的《律学新说》与《律吕精义》中关于等程律隔八相生的篇章，认为钱德明介绍的“749”定律法来自于朱载堉的《律吕精义》。［25］库特纳对朱载堉乃至中国古代律学的深入探究是非常值得肯定的，但他据此认为朱载堉的等程律隔八相生就是“749”调律法，这显然是一种误解。对此，引朱载堉在《律学新说》仅一句话就可以解释:“约率所谓七百四十九，即密率所谓七亿四千九百万有奇也。有奇是以密，无奇是以疏，此自然之理耳。”(［14］，135页)

朱载堉给出新法密率四种相生次序及方法后，又着意于横、斜、纵三种累黍尺下的四种相生计算:“横黍百分律，依新法算:黄钟长十寸;斜黍九十分律，依新法算:黄钟长九寸;纵黍八十一分律，依新法算:黄钟长八寸一分”(［1］，17～40页)他继续按照横、纵、斜三种累黍尺度完成四种相生共计十二次计算全部实现黄钟还原后，终于宣告:“是以新法不用三分损益，不拘隔八相生，然而相生有序，循环无端，十二律吕，一以贯之。此盖二千余年之所未有，自我圣朝始也，学者宜尽心焉。”(［1］，40页)在探求新律道路上，朱载堉始终坚持通过测音试验来度量弦线、律管的长短，因为定律的需要才借助算术方法，而不是因算术需要去限定律与度，这种观点现在看来都完全合乎律学计算之物理本质。［26］

朱载堉等程律计算精度达到25位，他用自制的八十一档大算盘完成了包括开方运算在内的大量计算，使得新法密率计算程序得以实践、计算结果高度精确。20世纪80年代美国华裔教授沈柏宏曾用现代计算机CDC CYBER-174⑤美国控制数据公司CDG(Control Data Cyber)20世纪70年代初生产的第四代电子数字计算机系统。验证了朱载堉的计算结果，他惊讶的说:“这的确是个谜，四百年前的人，怎么能算的这么精确!”(［16］，109页)这无疑是算盘与现代计算机跨越时空的一次较量，其重要意义在于朱载堉新法密率理论体系在数值分析思想上的对应及完备性。

6 余论

运筹帷幄在中国有着悠久的历史传统，朱载堉继承并发扬了这种传统，他精于律、历、算学等，在创立新律之初，重视这些学科之间的交叉关系，统筹规划，放眼全局，最终创立了新法密率。综合前述，朱载堉融合各学科之间的关系，清晰演绎算法流程的思路和缜密程序，可以得到如下流程图:

图5 朱载堉新法密率数值算法流程图

等程律数值算法流程图将《律吕精义·内篇》内容之相互关联以图表形式展现出来，从中可看到各章节的鲜明主题。图5中“内容方法”一栏，是各个章节的主题，“章节次序”和“步骤”被这些主题联系起来，从而直观体现出朱载堉工作的清晰脉络，追溯他创立等程律的思想轨迹。这些步骤既展现出朱载堉运用数值分析思维解决律学难题之缜密、超前组织模式，更体现他一丝不苟、敢于质疑的治学精神。通过进一步对朱载堉与西方斯蒂芬等人所创等程律路径差异进行比较研究，将更有利于逐个消除中、西方等程律创立过程的各种疑问，增进中、西方在该理论上的相互交流与融通。

1 朱载堉.律吕精义［M］.冯文慈点注.北京:人民音乐出版社，2006.

2 戴念祖.朱载堉—明代的科学和艺术巨星［M］.郑州:大象出版社，2008.67.

3 Kuttner F A.Prince Chu Tsai-Yu's Life and Work［J］.Ethnomusicology，1975，19(2):168 ～193

4 班固.汉书·律历志［M］//历代天文律历等志汇编.北京:中华书局，1976.1405

5 Chen Cheng Yih.Early Chinese Work in Natural Science［M］.Hong Kong:Hong Kong University press，1996.165

6 沈约.宋书·律历志［M］//历代天文律历等志汇编.北京:中华书局，1976.1667

7 范晔.后汉书·律历志［M］//历代天文律历等志汇编.北京:中华书局，1976.1454

8 缪天瑞.律学［M］.北京:人民音乐出版社，1996.54

9 魏征，等.隋书·律历志［M］//历代天文律历等志汇编.北京:中华书局，1976.1860～1861

10 陈其翔，陆志华.用分数逼近法研究三分损益律［J］.音乐艺术，1997，6(2):23～27

11 王光祈.东西乐制之研究［M］.上海:中华书局，1926.76

12 戴念祖.中国物理学史大系声学史［M］.长沙:湖南教育出版社，2001.188～221

13 杨荫浏.三律考［J］.音乐研究，1982，6(1):30～39

14 朱载堉.律学新说［M］.冯文慈点注.北京:人民音乐出版社，1986.

15 刘安.淮南子［M］.高诱注.北京:中华书局，1954

16 陈万鼐.朱载堉研究［M］.台北:台北故宫博物院，1992.52

17 Needham Joseph.Science and Civilization in China(Vol4.Part1)［M］.Cambridge:Cambridge University Press，1980.228

18 阮元校刻.十三经注疏上册·周礼注疏冬官考工记第六［M］.北京:中华书局，1980.278～279

19 徐飞.朱载堉十二平均律算法考［J］.科学技术与辩证法，1994，11(5):35～39

20 钱宝琮.中国数学史［M］.北京:科学出版社，1964.46～51

21 朱载堉.算学新说［M］//万有文库本.第一集735号.上海:商务印书馆，1931.

22 Stevin Simon.L’arithmetique［M］.Leyden，1585.

23 Stevin Simon.Vande Spoegheling der Singconst［M］//Edited by Fokker A D.The Principal Works of Simon Stevin:Engineering，Music，Civic Life．vol．5．Amsterdam:C.V.Swets ＆ Zeitlinger，1966.445 ～496

24 刘复.十二等律的发明者朱载堉［C］//国立中央研究院编.庆祝蔡元培先生六十五岁生日论文集，1933.279～310

25 Kuttner F A.The 749-Temperament of Huai Nan Tzu(+123B.C.)［J］.Asian Music．1975，6(12):88 ～112

26 黄国璽.朱载堉十二平均律理论创建中的律学数学方法［J］.音乐探索，1986，12(4):19～21