国内外煤炭价格弱式有效性的实证研究
2014-11-20雷强
雷 强
(神华科学技术研究院发展战略研究所,北京102211)
目前已有很多国内外学者对煤炭价格问题进行了相关研究。文献研究主要集中在煤炭价格的形成机制和历史进程、煤炭价格的影响因素、煤炭的价格预测、煤炭价格和原油价格之间的关系以及煤炭价格与煤炭下游需求行业之间的关系等方面。在煤炭价格的形成机制和历史进程方面,如Matthies(2005)、孟铁等人(2006)、曹海霞(2008)、刘劲松(2009)和张明华等人(2010)的研究[1-6]。在煤炭价格的影响因素方面,如谢守祥等人(2006)、吕松(2007)、谭章禄等人(2009)和徐宇航等人(2012)的研 究[7-10]。在煤炭价格预测方面,如张欢等人(2007)和李增光等人(2012)的研究[11-12]。在煤炭价格与原油价格之间关系研究方面,如战严领(2008)、张小军等人(2009)、何琬等人(2011)和连悄(2011)的研究[13-16]。在煤炭价格与煤炭下游需求部门之间的关系方面,如林伯强等人(2008)和杨军等人(2012)的研究[17-18]。在能源市场的市场弱有效性研究方面,魏学薛等人(2009)[19]对美国市场西德洲轻质原油价格与北海布伦特原油价格进行了市场有效性检验,结论表明国际石油价格收益率序列的残差序列不是独立同分布的序列,具有一定的非线性结构,拒绝市场弱有效性假说。
目前,关于煤炭价格的文献主要集中在以上几方面的研究中,但是国内外煤炭市场弱式有效性特征的研究不足。煤炭价格由于其价格体系和定价机制的多元化,价格影响因素和价格形成机制的复杂性,同时大量不同理性的煤炭市场多元化主体参与其中,煤炭价格的预测呈现出复杂性和综合性。煤炭市场是否具有弱有效性、煤炭价格时间序列是否服从随机游走的分布,对煤炭价格的长短期预测至关重要,但是目前关于煤炭价格预测方面的文献,只是关注于利用各种计量经济学等方法对煤炭价格进行预测,而没有考虑煤炭市场的弱式有效性问题。鉴于此,本文基于自回归检验、方差比检验和BDS法研究国内外煤炭价格的弱式有效性问题,为进一步寻找煤炭价格的内在规律性以及为今后的煤炭价格的预测提供一些有益的启示。
1 相关理论和研究方法
1.1 有效市场理论
有效市场假说(Efficient Markets Hypothesis,EMH)是由尤金·法玛于1970年提出的。有效市场的含义为:有效市场是这样一个市场,在这个市场中,存在着大量理性的、追求利益最大化的投资者,他们积极参与竞争,每一个人都试图预测单个股票未来的市场价格,每一个人都能轻易获得当前的重要信息。在一个有效市场上,众多精明投资者之间的竞争导致这样一种状况:在任何时候,单个股票的市场价格都反映了已经发生的和尚未发生、但市场预期会发生的事情,这也就是说如果一个市场是有效市场的话,那么该市场的相关价格是不可预测的。
根据法玛对三类有效市场的划分,分别是弱式有效市场假说、半强式有效市场假说和强式有效市场假说,不同有效程度的市场与不同类型信息即不同影响变量相关。其中弱式有效市场假说认为在弱式有效的情况下,市场价格已充分反映出所有过去历史的证券价格信息,包括股票的成交价、成交量,卖空金额、融资金额等,人们不可能靠该价格的历史信息去进行预测。本文采用以下方法联合检验国内外煤炭市场的弱式有效性,分别为序列相关检验的自回归模型、方差比检验和BDS法检验。
1.2 自回归模型
一个时间序列的自回归模型见式(1)。

模型中,Rt表示为第t期价格的收益率,Rt=(Pt-Pt-1)/Pt-1,P 为某一市场的价格或指数;βi为第t期与第t-1期收益率的自相关系数;εt为随机误差项。如果市场是弱有效的,由于收益率不存在滞后效应,故误差项不相关,即误差项是白噪音序列,其均值为零,方差为同方差。
1.3 方差比检验
方差比检验法是由Lo和 Mackinlay(1997)提出的用以检验时间序列是否呈现随机游走的检验方法。该检验方法认为如果时间序列符合随机游走假设的话,那么2期的方差应该是1期方差的2倍,是呈几何级数递增。方差比检验的标准正态分布统计量如果在某一显著水平下(一般指1%和5%显著性水平)大于相应的临界值,那么该时间序列就不符合随机游走假设,即拒绝该时间序列为市场弱有效性。方差比定义见式(2)。
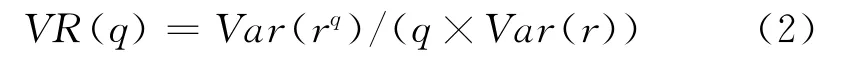
其中rq是q期的收益率,等于相应的一期收益率的之和,相应的同方差和异方差检验的正态统计量如式(3)所示。

f(q)是同方差假设的方差比渐进方差,f′(q)是异方差假设的方差比渐进方差。
1.4 BDS法
BDS统计量是Brock,Dechert和Scheinkman于1987年给出的一种检验时间序列非线性相关的方法。它基于Grassberger Procacia相关积分的概念建立起来的。BDS统计量定义如下所示。
接着计算关联积分C、K,见式(5)、式(6)。
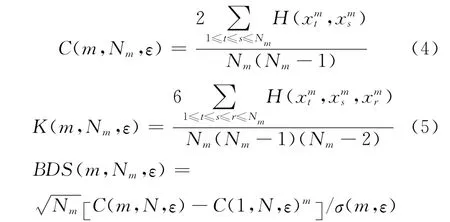
其中:m为嵌入维数;ε是包含时间序列点的m维球的半径;N为样本数目。σ(m,ε)定义

其中H(x)为Heiviside函数

在使用BDS统计量进行非线性检验之前须注意的是,需要消除原始时间序列的自相关的影响,通常对原始数据序列拟合AR(p)模型,在寻找到合适的阶数p后,计算AR(p)的残差序列并对该残差序列使用BDS统计量检验其是否为独立同分布。如果结果拒绝零假设,则意味着原始时间序列在某个显著水平下是内在非线性的,也不符合市场有效性假说。
2 实证研究
2.1 数据选择和处理
本文选取国内煤炭价格包括秦皇岛大同优混(Q5800K)(简称 Q5800K)、秦皇岛港山西优混(Q5500K)(简称Q5500K),国外煤炭价格包括澳大利亚BJ动力煤现货价(简称BJ)、欧洲ARA港动力煤现货价(简称ARA)、理查德RB动力煤现货价(简称RB)和纽卡斯尔NEWC动力煤现货价(简称NEWC)。由于缺乏国外煤炭价格的日数据,为了实证研究的一致比较分析,以上六种国内外煤炭价格都采用周数据,数据来源于WIND数据库。用于实证分析的是煤炭时间序列的对数收益率序列,这样可以将时间序列的趋势去掉。
2.2 数据的统计分析
由表1可以看出,Q5800K、Q5500K、BJ、ARA、RB和NEWC的收益率序列的峰度和偏度系数分别不等 于3 和 零。Q5800K、Q5500K、ARA、RB 和NEWC价格收益率的偏度小于零,说明高于平均收益率的天数要略多于低于平均收益率的天数,而BJ收益率的偏度大于0,说明高于平均收益率的天数要略少于低于平均收益率的天数。以上六煤炭价格收益率的JB统计量在1%的显著性水平下拒绝收益率服从正态分布的假定,且有“尖峰厚尾”特征。由此可以拒绝原假设,即以上六种煤炭周数据的收益率序列不服从正态分布,这同有效市场假说是相悖的。接下来运用基于自回归模型、方差比检验和BDS法对以上六种煤炭价格收益率进行有效性特征研究。
2.3 序列相关检验
本文使用的自回归模型如式(8)所示。

其中R为六种国内外煤炭价格的对数收益率,即Rt=ln(Pt/Pt-1),零假设为所有自回归系数都为零。在研究过程中滞后期选择为3期,自回归实证结果如表2所示。

表1 国内外煤炭价格收益率的描述性基本统计分析
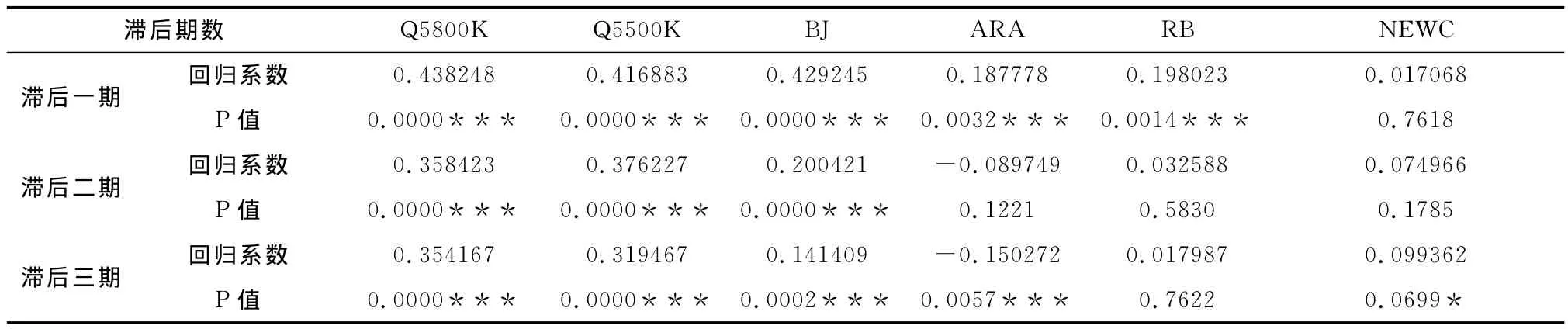
表2 国内外煤炭价格收益率的滞后1~3期自回归分析结果
从表2可以看出,国内2种煤炭价格Q5800K和Q5500K在1%的显著性水平下拒绝了随机游走假设,即国内煤炭市场不能得出弱式有效性的结论。在国外煤炭价格中,澳大利亚动力煤价格BJ在1%的显著性水平上拒绝了随机游走假设,即澳大利亚动力煤市场不能得出弱式有效性的结论。欧洲ARA港动力煤现货价和理查德RB动力煤现货价分别是滞后1期和3期以及滞后1期在1%的显著性水平下拒绝了随机游走假设,即欧洲ARA港动力煤市场和理查德RB动力煤市场不能得出弱式有效性的结论。而纽卡斯尔NEWC动力煤现货价只是在滞后3期在10%的显著性水平上拒绝了随机游走假设,纽卡斯尔NEWC动力煤市场弱式有效性的结论难以得出。因此,本文通过方差比检验和BDS法对上述六煤炭价格收益率进一步进行弱式有效性检验。
2.4 方差比检验
由于经济时间序列一般都会具有时变性和偏离正态分布,本文利用异方差条件下的方差比检验法进行市场弱有效性检验。本文选择的时间间隔为系统默认值,即q=2、4、8、16,分析结果见表3。

表3 国内外煤炭价格间隔2期、4期、8期、16期的方差比检验结果
从表3对国内外六种煤炭价格的方差比检验结果可以看出,在显著性水平1%上,国内外六种煤炭价格都不符合随机游走假设,因此不能得出上述六种煤炭价格达到市场弱式有效性的结论。
2.5 BDS法非线性特征检验
BDS检验在实际应用中需要适当选取ε。其中ε是判断白噪声的一个标准:ε取值太小会导致过多接受零假设,ε取值太大则会高估嵌入空间中向量间的贴近程度(Scheinkman & LeBaron,1989)。对于大样本(N>500)情况,Brock等(1992)建议的取值为序列标准差的0.5倍、0.75倍、1.0倍、1.5倍和2.0倍。在实际研究中,ε取值通常在序列标准差的0.5~2倍之间。因此,利用上述BDS统计分析法,ε取值为0.5、0.75和1.0,嵌入维数从2~10。
对上述六种煤炭价格进行BDS统计量非线性分析,得到相应的BDS统计量(表4)。从表4中可以看出,当ε=0.5、0.75和1.0等3个值,随着嵌入维数的不断增大,六国内外煤炭价格的BDS统计值均不断的增加,尤其是当ε=0.5时,BDS统计值快速的加大,这说明BDS统计均在5%的显著性水平下拒绝六种煤炭价格时间残差序列是独立同分布序列的IID假设(显著性水平α=5%,Zα=1.96),从而说明上述六种煤炭价格序列中存在非线性结构,并且可以明确拒绝市场弱有效性假说。同时可以指出的是,为了正确地描述煤炭价格时间序列的预测,必须使用非线性模型。
3 结论
本文利用国内外六种煤炭价格时间序列数据,分析了六种煤炭价格的市场弱有效性问题,通过自回归模型以及BDS法等方法对上述变量进行了实证研究,得出以下几点结论。
第一,国内外煤炭价格序列不服从正态分布,且有“尖峰厚尾”特征,这同有效市场假说是相悖的。国外四种煤炭价格的标准差大于国内两种煤炭价格的标准差,说明国际煤炭市场波动幅度和频率要大于中国煤炭市场,可能的原因在于国内煤炭价格市场化机制还不够完善,为了国民经济的平稳增长可能会对资源要素价格有所管制。
第二,从自回归模型检验结果看,除了纽卡斯尔NEWC动力煤市场弱式有效性的结论难以得出之外,其他五种煤炭价格在1%的显著性水平下拒绝了随机游走假设,即不能得出弱式有效性的结论。
第三,从方差比检验结果看,在显著性水平1%上,国内外六种煤炭价格都不符合随机游走假设,因此不能得出上述六种煤炭价格达到市场弱式有效性的结论。
第四,从BDS法检验结果看,国内外六种煤炭价格的BDS统计值均在5%的显著性水平下拒绝六种煤炭价格时间残差序列是独立同分布序列的IID假设,进一步说明上述六种煤炭价格序列中存在非线性结构,并且可以明确拒绝市场弱有效性假说。
从本文的实证研究表明国内外煤炭市场呈现出非线性特征并且拒绝煤炭市场是弱有效性市场,因此,目前的关于煤炭价格预测的研究文献通常使用的各种线形计量经济学模型的预测精度很难以提高。为了正确地进行煤炭价格时间序列的预测,必须使用非线性时间序列模型或高阶非线性计量经济学模型以及非线性动力学模型等非线性预测方法以便提高煤炭价格的预测精度。

表4 国内外煤炭价格的BDS法检验结果
[1]MATTHIES K.Commodity prices at record level[J].Intereconomics,2005,40(2):113-116.
[2]BHATTAC'HARYYAS C.Developments in the Coal Market[M].Energy Economics,2011:383-391.
[3]孟铁,霍喜福.国际煤炭市场价格变动影响因素分析[J].价格理论与实践,2006(6):55-57.
[4]曹海霞.我国煤炭价格的改革历程回顾及发展趋势前瞻[J].中国煤炭,2008(5):14-18.
[5]刘劲松.我国煤炭价格形成机制分析[J].煤炭经济研究,2009(2):6-8.
[6]张明华,赵国浩.煤炭价格形成机制存在的问题及对策分析[J].资源科学,2010(11):2210-2216.
[7]谢守祥,谭清华,宋阳.影响煤炭价格因素的相关性分析与检验[J].统计与决策,2006(11):57-61.
[8]吕松.煤炭价格影响因素的ISM分析[J].能源技术与管理,2007(5):127-131.
[9]谭章禄,陈广山.我国煤炭价格影响因素实证研究[J].改革与战略,2009(10):37-40.
[10]徐宇航,许遥.基于VAR模型的中国煤炭市场价格影响因素分析及预测[J].煤炭经济研究,2012(9):55-60.
[11]张欢,蒋佐斌.中国煤炭价格的ARIIVIA模型的建立及其预测分析[J].工业技术经济,2007(7):102-106.
[12]李增光,王晶,陆宁云,等.GMDH参数模型的改进及在煤炭价格研究中的应用[J].系统工程,2012(6):105-111.
[13]战严领.国际油价走势及对国内煤炭价格的影响分析[J].中国煤炭,2008(9):21-25.
[14]张小军,石明明.基于误差修正机制的能源价格联动性研究—以国内煤炭与国际原油为例[J].中国物价,2009(11):30-34.
[15]何琬,卢小舒.煤炭价格与石油价格的波动溢出效应分析[J].工业技术经济,2011(11):66-71.
[16]连悄.我国煤炭价格与原油价格关系的协整研究[J].经济与社会发展,2011(9):8-12.
[17]林伯强,牟敦国.能源价格对宏观经济的影响—基于可计算一般均衡(CGE)的分析[J].经济研究,2008(11):88-101.
[18]杨军,宋学锋.煤炭价格对我国各相关产业的影响研究—基于投入产出分析[J].经济问题,2012(11):33-36.
[19]魏学薛,任彪.国际原油价格非线性结构的BDS检验[J].统计与管理,2009(1):57-58.
