结合CAD 二次开发精确求解空间预应力束引伸量
2014-11-18马天乐
马天乐
(同济大学建筑设计研究院(集团)有限公司,上海 200092)
桥梁设计及施工中,预应力束的张拉一般釆用张拉力和引伸量双控,因此预应力束引伸量的求解是很重要的。但是在实际施工中发现实际的引伸量值与引伸量计算值误差过大,解决这个问题一方面是要求理论计算中参数的取值与实际值一致,另一方面也要求计算值是精确的,满足工程要求精度的。目前的引伸量计算更多的是基于平面内曲线的,当实际工程中的钢束往往有平弯或曲面内的曲线,如何精确求解这类空间曲线是本文的主要目的。
本文结合AutoCAD 的二次开发功能提出一种快速、直观、准确的计算空间复杂形状预应力束引伸量的方法。Arx.Net 二次开发是AutoCAD 2006 及以后版本都支持的新的AutoCAD 二次开发工具。该方法基于Microsoft.Net,是目前主流编程方法,也是今后的发展趋势。与其他开发方式相比该开发方式有开发速度快,运行速度快,自动按需加载,程序不会导致内存泄漏,健壮性好等优点。本文介绍了结合Arx.Net 二次开发计算复杂形状预应力束的引伸量的方法。
1 在AutoCAD 中计算任意空间预应力束引伸量的方法
1)空间曲线预应力引伸量计算。
根据桥梁规范[1,2],预应力束在张拉过程中,任意一点处的应力为:
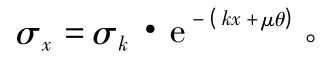
其中,σk为锚下控制张拉应力;k 为管道线摩阻系数;x 为张拉端到计算点预应力束空间长度;μ 为管道角摩阻系数;θ 为张拉端到计算点预应力束空间转过的角度。
采用某点处微单元计算,如微单元起点钢束应力为σ1,则微单元终点的钢束应力为:

计算微单元引伸量方法为:

其中,Es为钢束弹性模量;s 为微单元长度。此外,微单元引伸量如果用平均应力求解将会有比较大的误差。
2)空间曲线微段的空间转角计算。
在求解应力和引伸量的过程中,需求解曲线微段的空间转角,以往手工计算,这一项几乎很难做到,利用AutoCAD 的功能我们可以轻松的计算空间转角。AutoCAD 中的曲线,包括直线、圆弧、多义线、样条曲线等都有共同的基类Curve(Arx 中为Acdb-Curve),求解空间转角就可以利用Curve 对象的函数GetFirstDerivative(distance),该函数得到的是曲线在某个位置的一阶导数,输入的参数distance 表示距离起点的长度,返回的结果表示是一个向量Vector3d,利用该功能求出微段起始点和终止点的一阶导数,就可计算出该曲线微段的空间转角。
3)计算钢束应力的代码实现。
参数Curve——代表的是钢束曲线,该曲线是空间曲线;
参数LenX——代表的是曲线的长度,这个长度可以是整根曲线的长度,也可以是曲线部分的长度,返回的值是曲线到该段长度处的应力;
参数IsYL——返回曲线段的终点处应力,还是返回终点处的引伸量值;

2 各种条件下预应力束引伸量的求解
1)单端张拉。
由上述方法,可求得空间束上,任意微小段的曲线长和该段微小转角,利用式(1)逐段递推,可以求出任意微段上的空间转角和应力,由式(2)求得该微段的引伸量,将每个微段引伸量累加,就得到了单端张拉空间预应力束的引伸量。
2)双端张拉。
若预应力束为不对称双端张拉,则两端的引伸量需分别求解,问题的关键在于如何找到变形不动点。不对称预应力束的变形不动点位置是个非常复杂的问题,在实际张拉过程中,受两端千斤顶行程速度、功率以及管道摩阻的不均匀性等影响,无法预知真正的不动点。
一般理论计算时,假定左右两端分别向不动点计算摩阻损失,得到的量值相等,也就是不动点左右面的应力应该相等。由于预应力束是一条空间光滑曲线,任意一端向另一端求摩阻损失的函数,应该是单调、连续、光滑的,见图1。

图1 不对称空间束单向摩阻损失曲线
由此可见,这两条摩阻损失曲线必然有交点Xd,也就是不动点。电算过程中,可以先假定不动点的位置在钢束的中点,由两端分别向不动点求单端张拉的累计摩阻损失,然后采用二分法,不断循环,使得两端摩阻计算值趋于相等。由于这两条曲线为连续、光滑、单调的,所以这个迭代过程必定是收敛的,最后便可求出真正的不动点位置。求出不动点位置后,左右两端的引伸量只要分别釆用单端张拉求解法便能得出。
对于预应力束对称且为双端张拉的情况,也只是上述情况的一个特例,算法无需改动,这样编写代码统一更易于理解和维护。
3)直线梁斜腹板内预应力束引伸量的求解。
AutoCAD 中用多义线描述钢束,则该线本身即为三维曲线,理论上可以描述任何复杂形状的预应力束型,但是实际上要求用户绘制出三维曲线是很困难的。
直线梁斜腹板内预应力束引伸量的求解:让用户绘制出斜腹板在竖直截面上的投影,再给出腹板的斜率,程序自动计算出各个控制点的三维空间坐标,再对该三维曲线计算求解引伸量。
曲线梁斜腹板内预应力束引伸量的求解:对于在圆曲线上的等截面连续梁,要求用户给出斜腹板斜率和梁中心线曲率,可以计算出钢束任意一点的平面曲率,由此可以计算出钢束任意一点的空间坐标。此时需要注意,由于平面曲线的影响,钢束线形为在一个圆台表面的曲线。
通用方法:这里作者采用的方法是通过程序生成的样条曲线。按照笛卡尔坐标系,向上为Z 轴,先按照某个步长求出曲线在XOY 平面上的点,再根据曲线的竖弯求出对应的Z 坐标。这样就形成了一条空间的曲线。此时在CAD 中可以用样条曲线拟合的方法得到该曲线。按此方法求出样条曲线后,按本文前面所述一般的方法计算钢束引伸量。
3 采用空间曲线与直线算法进行比较
分别取如图2 所示平面曲线①组A,B,C 三根钢束和曲面曲线②组A',B',C'三根进行引伸量计算。曲面曲线②组钢束取直线钢束投影在半径为500 m 的曲面上,②组曲线的展开长度等于①组曲线。计算参数取值:摩阻系数μ=0.16,管道偏差系数k=0.001 5,张拉控制应力为1 395 MPa。采用两种方法计算的引伸量见表1。

图2 钢束平面曲线图
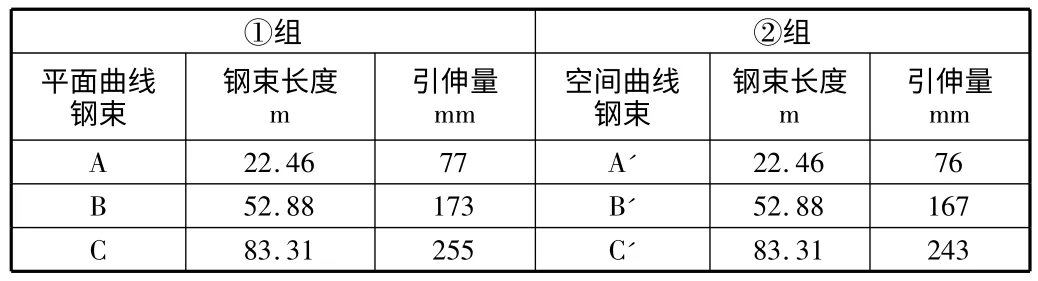
表1 引伸量计算结果表
由此可见,采用直线计算而忽略平面曲线的计算是存在一定误差的,并且误差随着曲线长度增加而增加。
4 结语
对于负责线形的曲线,手工计算引伸量的工作复杂且困难,采用AutoCAD 二次开发的方法,使计算快速、易于操作,而且精度更高,在实际应用中取得了较好的效果。
[1]JTG D62-2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].
[2]龚建峰,张 瑾.空间曲线预应力束几何计算[J].华东公路,1997(2) :92-93.
[3]肖 军,徐秀芳.任意空间预应力束引伸量实用CAD 电算求解法[J].盐城工学院学报(自然科学版),2005(2) :40-42.
[4]范立础.预应力混凝土连续梁桥[M].北京:人民交通出版社,1999.
