基于结构成分双向扩散的图像插值算法

贾 茜易本顺 肖进胜

(武汉大学电子信息学院 武汉 430072)

1 引言

图像插值(放大)是指提高数字图像的分辨率，又称为图像上采样，其目的是使图像尺寸变大、像素点增加，且不产生明显的边缘模糊和锯齿。它在军事、遥感、航天、气象、监控、生物医学、电子消费品等诸多领域有着广泛的应用，是图像显示、传输、理解等方面的基础。通常，图像插值中输入的低分辨图像可以看作是高分辨率图像受到成像系统点扩散函数(Point Spread Function, PSF)的作用，并下采样得到，因此上采样就是求解高分辨率图像的过程。

传统的图像插值方法是用一些空间不变的已知函数逼近原图像，如：最近邻域点插值、双线性插值、多项式插值和样条插值及其改进算法[1,2]等。这些方法简单、易于实现，在一些常规的图像尺寸转换而对插值图像质量要求其次的场合能取得较好的应用，但是这些方法存在不同程度的边缘模糊、锯齿或块效应。为了克服这些方法的缺陷，出现了边缘自适应插值方法。随着图像去噪、复原、修补、增强、超分辨重建等技术的不断发展，这些研究领域中许多数学方法具有通用性和交叉性, 它们也被用到图像超采样中来，如：基于偏微分方程[3]、全变分方法[4]、贝叶斯方法[5]、核回归方法[6,7]、非局部平均(Non Local Means, NLM)滤波方法[8]、基于小波变换的方法[9]、机器学习的方法[10]、基于稀疏表示方法[11]等。在业界，有一些成熟的商用软件已经被广泛使用，如OnOnes Perfect Resize Pro，以及Adobe PhotoShop的插件Genuine Fractals Print Pro和Alien Skin Blow up等，都取得了良好的效果。图像插值领域目前的研究趋势是综合运用各种方法，以获得更加清晰的插值图像。

由于边缘自适应非线性插值方法相较之传统的线性插值方法具有更好的边缘保持效果，因而成为研究的热点。已有的边缘自适应插值算法大致可以分为两类：基于原始图像边缘的自适应插值方法和基于插值后图像边缘增强的方法。第1类是在低分辨率中先进行边缘检测，然后对于平坦区域和边缘采取不同的插值策略[12,13]。文献[14]提出的基于轮廓模板(contour stencils)的图像插值算法是近年来出现的较优秀的边缘自适应算法之一，该方法对图像边缘和几何结构具有更好的适应性，但是由插值过程本身引起的插值图像中的边缘扩散问题并未得到好的解决。第2类方法是在传统的插值方法得到初始高分辨率图像后，利用低分辨率图像中边缘先验作为约束[15]，或者通过锐化增强型滤波器[16,17]来对边缘及附近像素做处理以增强边缘。冲击滤波器[18]能够增强图像边缘，将其用在图像插值中能显著提高插值图像锐度，但是它对噪声比较敏感，而耦合双向扩散模型[19]能在边缘实施双向扩散，为边缘增强提供了良好的原始模型，然而该模型对不同梯度模值的边缘自适应性较弱，因而会产生锯齿和人工痕迹。

针对传统的一步插值的图像放大算法边缘扩散问题，在考察了两类边缘自适应插值方法各自的优势的基础上，本文提出了一种融合了边缘自适应插值和双向扩散滤波增强处理的插值框架，以进一步提高插值图像清晰度，减小边缘扩散程度。在边缘增强处理中，改进了原始耦合双向扩散模型，并引入形态成分分解(Morphological Component Analysis, MCA)模型分解提取几何结构分量再实施滤波。实验表明，本文方法能有效减小边缘扩散程度、提高图像锐度，并且边缘光滑、过渡自然，避免了产生边缘锯齿和过度的人工效应。

2 本文算法

如前所述，轮廓模板插值算法是一种基于全变分的边缘轮廓自适应的非线性插值方法[14]，由于它对边缘轮廓形状的精细划分和复杂的插值策略，使得该方法对图像边缘和几何结构具有很好的适应性。尽管轮廓模板插值在抑制边缘锯齿、振铃以人工痕迹等方面均表现良好，但是由插值过程本身引起的插值图像中的边缘扩散问题并未得到好的解决，使得插值图像锐度有限。

因此，考虑将基于原始图像边缘的自适应插值方法和基于插值后图像边缘增强的方法两者结合，即首先由轮廓模板插值得到初始高分辨率图像之后，再对边缘进行增强以提高图像清晰度。而传统的锐化方法，如拉普拉斯算子锐化，是加强边缘“对比度”，而非减小边缘“宽度”，其次会将图像中的噪声一并凸显出来。而双向扩散滤波器可以在反向扩散锐化边缘的同时去噪声，故本文采用双向扩散滤波器实现插值后边缘增强的过程。由此，设计了如图1所示的插值算法框架。

算法框架的核心部分包括轮廓模板插值和边缘增强两个部分。在边缘增强处理中，由于反向扩散的冲击滤波器首先要检测边缘，而图像中的纹理和噪声可能会对边缘检测过程有影响进而造成滤波增强后图像失真，而正向扩散会模糊图像中的纹理细节，故而考虑先将图像作 MCA模型[20]分解，待分离出几何结构分量之后再对结构成分实施边缘增强处理。同时，改进了反向扩散模型，使其能根据边缘梯度自适应地调整边缘扩散程度，且更加柔和地控制梯度方向的灰度值变化。本文方法在轮廓模板插值的基础上，减小了边缘扩散程度，使放大后的图像清晰度进一步得到提升。下面详细阐述本文方法原理和步骤。

2.1 双向扩散原始模型分析

图1 本文算法流程框图

轮廓模板插值算法仍避免不了插值本身引起的边缘扩散问题，尤其在放大倍数较大时更为明显。图2(a)显示了斑马图片经轮廓模板插值的结果，其缩放因子为4，即16倍放大。通过下面的局部放大特写可以看到图像边缘较宽、整体清晰度有限，因此还需要对边缘做处理以进一步提高图像锐度。而传统的锐化方法，如拉普拉斯算子锐化，是在一定程度上加强边缘对比度，而非减小边缘“宽度”，其次会将图像中的噪声一并凸显出来。故还需要设计新的增强边缘滤波器，以提高图像锐度。

基于偏微分方程(Partial Differential Equation,PDE)的图像冲击滤波方法[18,19]在图像去噪、去模糊等研究方向有着广泛应用，它可以明显减小边缘扩散程度。经典的冲击滤波PDE模型为

其中，tu是图像的解，t为迭代次数，0u为输入图像。sign表示符号函数。η表示沿梯度u∇方向，则

式(2)中梯度方向二阶导数uηη可以看作是一个边缘检测器，冲击流发生在处，经过冲击滤波器，信号将在原有拐点处形成剧烈跳跃，从而得到图像锐化效果。图2显示了冲击滤波前后的对比效果，可以看到经过锐化型冲击滤波器后边缘变窄了，图像更加清晰。

然而，冲击滤波模型对于图像中的噪声很敏感，且由符号函数产生的阶跃特性会使锐化图像中产生锯齿和人工效应。为了降低冲击滤波器的噪声敏感性和边缘锯齿，Alvarez和Mazorra提出了将正向扩散滤波与冲击滤波相耦合的双向扩散模型[19]：沿边缘梯度方向反向扩散以增强边缘，而沿梯度切线方向正向扩散以去除人工锯齿，PDE表达如下：

其中，Gσ是标准差为σ高斯函数， c为正常数，ξ表示梯度切线方向，为正向扩散算子：

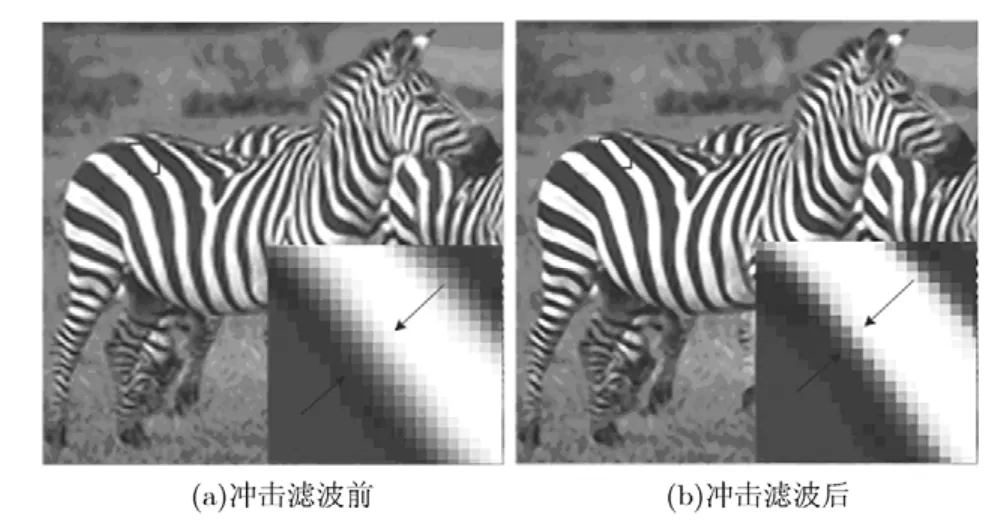
图2 斑马图片插值引起的边缘扩散和冲击滤波处理后对比

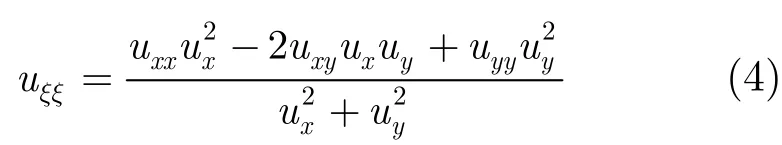
式(3)由锐化边缘的冲击滤波项和平滑轮廓的扩散项两者耦合而成。冲击项中通过高斯函数Gσ与uηη卷积，减少了噪声的影响，正向扩散项通过系数c调节平滑权重。该模型在平滑噪声的同时锐化边缘，然而模型中延用了符号函数形成冲击流，仍会在原有的拐点处形成跳变，插值图像中可能会出现边缘锯齿；且不同的扩散权重迭代结果可能会出现锐度不够或者过度而产生过冲、油画效应等不良影响。

2.2 基于结构成分双向扩散的边缘增强

2.2.1改进的耦合双向扩散模型 尽管双向扩散模型能增强图像边缘和细节，但会产生图像失真。图 3显示了对 Lena初始放大图像进行双向扩散增强边缘的效果，处理后的效果如图3(b)所示，左上角是方框内的局部放大图。尽管图像整体清晰度在主观上有所提高，但从局部放大图中可以看到明显锯齿效应，如眉毛边缘不够光顺；且图像稍显不自然，有油画的感觉。

为此，本文提出改进模型为

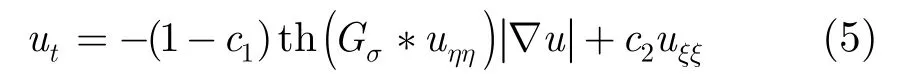
其中

式中1c为自适应调节函数，k为调节系数；th为双曲正切函数，。

图3 利用双向扩散对Lena初始放大图像边缘增强效果

其次，冲击项将使原本灰度值小的一侧像素值进一步减小，而将灰度值大的一侧灰度值进一步增大，这样使灰度差的变化速率加大，从而得到锐化边缘和细节的效果。由于冲击项中的符号的阶跃响应特性，容易造成过冲，边缘梯度的剧烈变化会凸显边缘锯齿或产生过冲。 所以，本文在模型中利用双曲正切函数代替了原始的符号函数，函数在原点两边变化稍缓和，如图4所示，这样能削弱符号函数在边缘产生的剧烈突变，使边缘两边像素值的变化更加柔和，进一步减轻锐化的人工痕迹。

对式(5)采用有限差分法求解[21]，离散化的数值计算迭代形式为

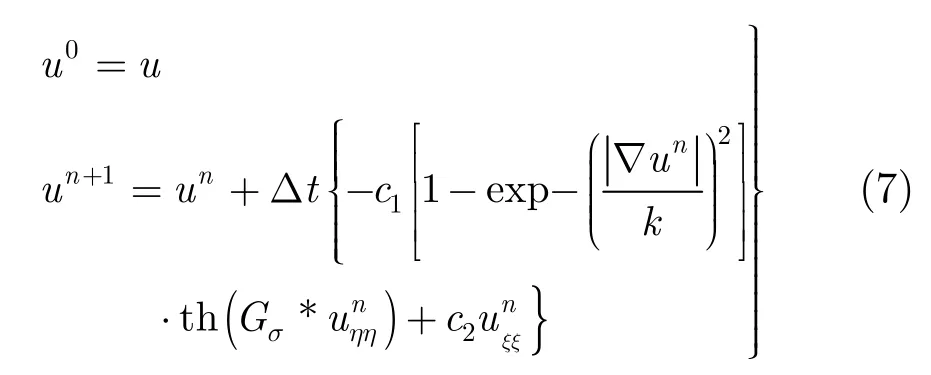
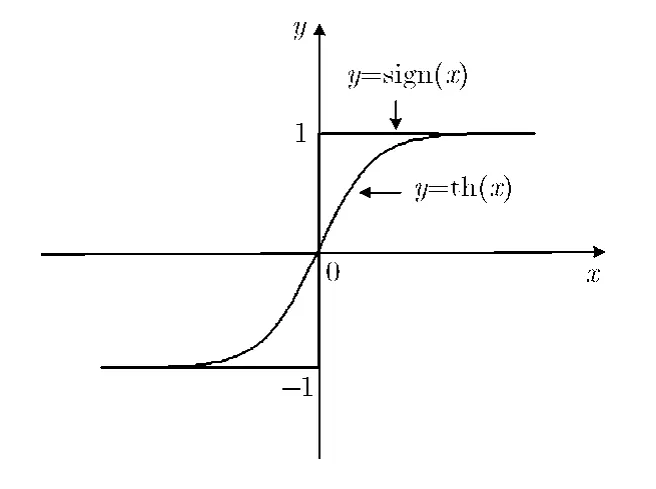
图4 符号函数与双曲正切函数

2.2.2结构成分提取 在双向扩散模型中，图像中的纹理及随机噪声会对其冲击项中二阶导数过零点检测产生影响，而正向扩散会模糊图像中的纹理细节。根据Meyer图像模型理论，自然图像可以分解为卡通部分和纹理部分，其中卡通部分由分片光滑的区域和清晰的边缘构成。由此，考虑先将图像卡通部分即结构成分提取出来，再实施双向扩散滤波过程。

文献[20]提出一种将图像分解为 “几何结构”、“振荡或纹理”、“噪声和残差”的多形态分量分解模型。MCA的基本思想是利用两个预先设定的字典，分别来描述纹理部分和结构部分，通过交替最小化目标泛函求解，并计算残差噪声，从而实现图像分解。MCA变分框架为

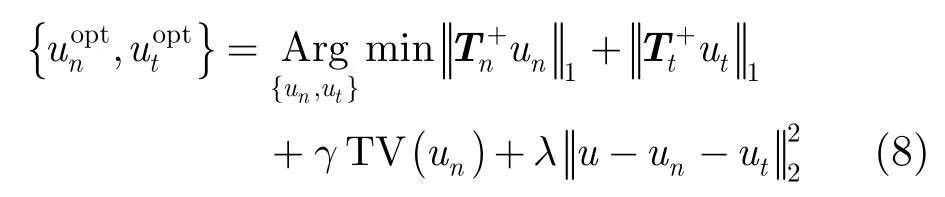
其中，nu和tu分别为待求的结构分量和纹理分量，和分别为结构分量和纹理分量稀疏表示字典下的过完备线性变换。由模型可知，MCA框架包含3个重要部分：前两项为纹理和结构分量的稀疏性度量项(经典MCA采用1l范数)；为结构部分的正则化先验模型(经典 MCA采用全变差先验)；为数据保真项。对于结构分量，可以选用能够稀疏表示平滑部分的字典，如：小波(Wavelet)、曲线波(Curvelet)、脊波(Ridgelets)、轮廓波(Contourslets)等变换。对比“基于稀疏表示的图像分解”和“基于变分方法的图像分解”，MCA方法结合了这两种方法的优点，可以将图像几何结构、纹理和噪声更加精确地分离。

为了使本文提出的改进的双向扩散滤波更精确地作用于边缘轮廓，先利用 MCA模型将初始高分辨率图像I分解为两部分：，如图5所示，其中代表几何结构部分，为的补集，代表其它部分。待分离之后，单独对实施上一节所述的双向扩散滤波，可以有效避免纹理、噪声对图像梯度方向二阶导数零交叉点检测的干扰，以及正向扩散造成的细节模糊。分解处理的是灰度图，若为彩色图像，则将其转换成YCbCr色彩空间，对Y通道分解。然后，再将处理后的结构部分和其他部分进行像素级合成，对于彩色图像则将处理后的Y通道与原始CbCr反转换，得到最终的输出结果。利用本文提出的结构成分双向扩散与原始双向扩散滤波对初始高分辨率图像处理结果对比如图6所示，可见经原始模型处理后百叶窗边缘锯齿效应严重，而本文提出的方法边缘平整、清晰，锯齿效应得到明显改善。

图5 MCA模型分解示意图

图6 结构成分双向扩散与原始双向扩散滤波结果对比

2.3 本文算法实现步骤

本文算法结合了边缘自适应插值和插值后图像边缘增强两类方法各自的优势，提出了对轮廓模板插值图像进行结构分量双向滤波的插值框架。具体处理步骤为：首先，对原始输入的低分辨率图像用轮廓模板插值算法放大；然后，将得到的初始高分辨率图像利用 MCA模型分解为结构部分和其他部分；再对其中的结构分量实施改进的双向滤波以增强边缘轮廓；最后，将处理后的结构部分和其他部分合成，得到最终的边缘增强的高分辨率图像。

本文提出的改进的双向滤波模型数值实现步骤如表1所示。

表1 改进的双相滤波模型数值实现步骤

3 实验结果与讨论

实验选取了各种尺寸大小的标准测试图及自然拍摄的大量图像来验证本文算法的有效性。对比算法包括双三次插值、新边缘导向插值(New Edge-Directed Interpolation, NEDI)[13]、原始的基于轮廓模板插值算法[14]，以及3种广泛应用的图像缩放软件：(1)OnOne Perfect Resize Professional Edition v7.0专业版，它是图像无损放大和调整的工业标准软件，在摄影及印刷业有很高的知名度；(2)Genuine Fractals Print Professional v5.0，它是一款Adobe Photoshop分形及打印插件，能创建高质量、易于打印的图像文件；(3)Alien Skin Blow up v3.0，它是一款高质量的图像无损放大插件，支持16倍甚至36倍放大而不产生明显的修饰痕迹。

实验中，首先将原始输入图下采样得到低分辨率图像，然后利用本文方法以及其它3种算法和3种插值软件进行放大处理到原始尺寸。缩放因子为4，即长宽各放大4倍，整体图像放大16倍。式(6)的模型参数为：；高斯模糊核参数为(7, 10)。客观评价标准采用峰值信噪比(Peak Signal of Noise Ratio, PSNR)和结构相似度(Structural Similarity Index Measurement,SSIM)，并结合主观视觉效果来评价图像质量。

PSNR值的计算公式为

表2列举了5个不同类型的标准测试图不同算法插值得到的PSNR和SSIM。可以看出本文提出的方法在7种对比算法中客观质量最优，而对比原始的轮廓模板插值算法，PSNR和SSIM均有提升。

表2 不同方法客观指标对比(每个单元有两行数据，上一行表示PSNR，下一行表示SSIM)

图7显示了Airplane和Child两幅图像主观效果。每幅图右下角是用图片查看器分别对图 7(a1)和图 7(b1)方框区域放大的局部截图。可以看到 7种方法获得的图像边缘光滑和扩散程度均有所不同。Airplane图像局部截图放大可以看到飞机尾部边缘和数字，本文方法明显减少了边缘扩散程度，即边缘更窄了，边缘锐度相较之其他算法有所提升。对 Child图像各种算法所生成的插值图像在小孩的眼睛和脸部轮廓部分有显著区别，且3种插值软件得到图像有粗糙的颗粒感，本文方法与其他3种插值算法结果则较为平滑，而本文方法明显提高了曲线边缘锐度。从整体上看，本文方法清晰度最高，并且由于冲击项的改进，边界部分过渡自然，没有明显的人工效应。

实验从客观指标和主观质量两方面评价了不同插值算法的效果，可以看到本文提出的基于结构成分冲击滤波的插值方法能够明显减轻边缘扩散程度，放大图像质量更好。

4 结束语

本文提出了一种基于结构成分冲击滤波的图像插值算法。该算法结合了边缘自适应和插值后增强两类方法各自的优势，充分利用了原始低分辨率图像自身的边缘轮廓信息，综合应用轮廓模板插值、MCA分解以及双向扩散滤波来得到高分辨率图像。在边缘增强过程中，通过提取结构成分及改进耦合双向滤波器的模型，使其能够根据边缘梯度自适应地调整边缘扩散程度，并且更加柔和地控制梯度方向的灰度值变化。通过实验证明了本文方法的有效性，相比于传统的插值、相关的边缘轮廓自适应插值以及几种应用普遍的图像放大商用软件，本文方法不仅能有效提高边缘锐度，并且过渡自然，不会引入锯齿效应或者明显的人工效应，产生了更加优越的主客观图像质量。

图7 7种图像插值放大方法效果对比

[1] 陈瑶, 孙兴波, 黄祥, 等. 一种消除锯齿的图像放大算法[J].四川理工学院学报(自然科学版), 2013, 26(3): 35-37.Chen Yao, Sun Xing-bo, Huang Xiang, et al.. An Algorithm of anti-aliased image magnification[J]. Journal of Sichuan University of Science ＆amp; Engineering (Natural Science Edition), 2013, 26(3): 35-37.

[2] 陈利平. 自适应 Catmull-Rom 样条图像放大[J]. 计算机辅助设计与图形学学报, 2013, 25(2): 200-207.Chen Li-ping. Image amplification based on adaptive Cammull-Rom interpolation[J]. Journal of Computer-Aided Design ＆amp; Computer Graphice, 2013, 25(2): 200-207.

[3] 席志红, 海涛, 肖易寒. 基于混合非线性偏微分方程扩散的可逆图像放大[J]. 系统工程与电子技术, 2013, 35(5): 1098-1103.Xi Z H, Hai T, and Xiao Y H. Reversible image interpolation based on hybrid anisotropic partial differential equation diffusion[J]. Systems Engineering and Electronics, 2013, 35(5):1098-1103.

[4] Aly H and Dubois E. Image up-sampling using total-variation regularization with a new observation model[J]. IEEE Transactions on Image Processing, 2005, 14(10): 1647-1659.

[5] Babacan S D, Molina R, and Katsaggelos A K. Variational Bayesian super resolution[J]. IEEE Transactions on Image Processing, 2011, 20(4): 984-999.

[6] Hiroyuki T, Farsiu S, and Milanfar P. Kernel regression for image processing and reconstruction[J]. IEEE Transactions on Image Processing, 2007, 16(2): 349-366.

[7] 周鑫, 胡访宇, 朱高. 基于核回归的正则化超分辨率重建算法[J]. 电子测量技术, 2012, 35(3): 62-68.Zhou X, Hu F Y, and Zhu G. Super-resolution reconstruction based on adaptive kernel regression[J]. Electronic Measurement Technology, 2012, 35(3): 62-68.

[8] 李家德, 张叶, 贾平. 采用非局部均值的超分辨率重构[J]. 光学精密工程, 2013, 21(6): 1576-1585.Li Jia-de, Zhang Ye, and Jia Ping. Super-resolution reconstruction using nonlocal means[J]. Optics and Precision Engineering, 2013, 21(6): 1576-1585.

[9] 冯象初, 姜东焕, 徐光宝. 基于变分和小波变换的图像放大算法[J]. 计算机学报, 2008, 31(2): 340-345.Feng X C, Jiang D H, and Xu G B. Combining variation and wavelet transform for image zooming[J]. Chinese Journal of Computers, 2008, 31(2): 340-345.

[10] Lu X, Yuan Y, and Yan P. Image super-resolution via double sparsity regularized manifold learning[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2013, 23(12):2022-2033.

[11] Yang J C, Wright J, Huang T S, et al.. Image super-resolution via sparse representation[J]. IEEE Transactions on Image Processing, 2010, 19(11): 2861-2873.

[12] 孙士保, 段建辉. 一种基于边缘梯度的图像插值算法[J]. 计算机工程, 2013, 39(8): 239-242.Sun Shi-bao and Duan Jian-hui. An image interpolation algorithm based on edge gradient[J]. Computer Engineering,2013, 39(8): 239-242.

[13] Li X and Orchard M T. New edge-directed interpolation[J].IEEE Transactions on Image Processing, 2001, 10(10):1521-1527.

[14] Getreuer P. Contour stencils: total variation along curves for adaptive image interpolation[J]. SIAM Journal on Imaging Sciences, 2011, 4(3): 954-979.

[15] Sun J, Sun J, Xu Z B, et al.. Image super-resolution using gradient profile prior[C]. IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2008, Anchorage,USA, 2008, 1: 2471-2478.

[16] 计忠平, 方美娥, 王毅刚, 等. 保持边缘特征和增强对比度的图像缩放算法[J]. 中国图象图形学报, 2012, 17(2): 178-182.Ji Z P, Fang M E, Wang Y G, et al.. Edge-preserving and contrast-enhance image scaling[J]. Journal of Image and Graphi, 2012, 17(2): 178-182.

[17] 杜月林, 韩小萱. 基于边缘检测的图像超分辨率重建研究[J].国外电子测量技术, 2012, 31(10): 22-26.Du Yue-lin and Han Xiao-xuan. The research of super-resolution image reconstruction based on edge detection[J]. Foreign Electronic Measurement Technology,2012, 31(10): 22-26.

[18] Osher S J and Rudin L I. Feature oriented image enhancement using shock filters[J]. Journal on Numerical Analysis, 1990, 27(4): 919-940.

[19] Alvarez L and Mazorra M. Signal and image restoration using shock filters and anisotropic diffusion[J]. Journal on Numerical Analysis, 1994, 31(2): 590-605.

[20] Starck J L, Moudden Y, Bobin J , et al.. Morphological component analysis[J]. Proceedings of the SPIE, 2005, 5914:209-223.

[21] 肖进胜, 冯慧, 易本顺, 等. 半线性抛物型微分包含的有限差分法[J]. 武汉大学学报(理学版), 2006, 52(3): 262-266.Xiao Jin-sheng, Feng Hui, Yi Ben-shun, et al.. Finite difference method for semi linear parabolic differential inclusions[J]. Journal of Wuhan Vniversity (Natural Science Edition), 2006, 52(3): 262-266.