综合运输体系下城市公路网络布局方法研究
2014-11-17姜镇
姜 镇
(太仓市公路管理处,江苏 太仓 215400)
0 引言
近年来,我国城际高速铁路、城市轨道交通、水运等运输方式快速发展,要形成良好的综合运输局面,就要求公路运输与其他方式密切配合,通过合理衔接,形成现代化的综合运输体系,充分发挥各种交通运输方式的优势,通过和多种运输方式的集成提高综合效率[1]。
公路交通机动、灵活的运输特点决定了它在综合交通体系中的重要作用,其布局既要考虑与其他运输方式站场的有效衔接,又要保证良好的路网可达性。因此,有必要对已有的公路网布局方法进行研究完善,使之与发展综合运输体系的要求相适应。
1 公路网络布局方法概述
目前,具有代表性的公路网布局规划理论与方法主要有五类:四阶段法、总量控制法、交通区位法、节点布局法和动态规划法[2][3][4]。
(1)四阶段法
通过发生量和吸引量预测、OD分布预测、运输方式分担预测和交通量分配,预测得到区域路网交通量,以此作为路网布局设计的主要依据,对规划方案进行评价和比选。其有效性较多依赖于现状OD分布的准确性,分析结果强调以改善交通运行状况为目的进行网络和线路规划。
(2)总量控制法
在分析现状路网和交通特征的基础上,根据社会经济发展状况和运输量的变化特征,得出公路网建设总规模,再以路网规模总量为约束条件,根据区域内社会经济发展和生产力分布特点,求解最优路网。这种方法研究区域的综合经济规模分布与运输网络形态之间的关系,是一种定性与定量分析相结合的规划方法。
(3)交通区位法
从经济地理出发,研究规划区域的交通区位线,即交通现象在地理上的高发地带的原理线,根据交通区位线网络,结合交通节点情况、地理约束条件等因素,确定交通运输线走向。根据产业社会背景及交通吸引特征,研究交通线的运输方式配置,确定公路路线。
(4)节点布局法
通过分析路网节点和选择节点间路线形成规划路网的布局,其核心是通过对交通、经济要素的综合考虑建立节点重要度模型和节点间连线重要度模型,以此作为网络布局的依据。这种方法能够比较好地解释土地利用、交通需求与交通设施之间的关系。
(5)动态规划法
通过建立以运输成本等为目标函数、以路网规模和资金为约束条件构成的优化模型,根据规划目标,研究多种可能方案,将各种方案输入模型,选择适当的优化算法,求解优化模型,获得实现优化目标的路网布局方案。
2 综合运输体系下城市公路网布局方法
综合运输体系是指在社会化的运输范围内和统一的运输过程中,按照各种运输方式的技术经济特点,形成分工协作、有机结合、布局合理、联结贯通的交通运输综合体,它是社会经济发展到一定阶段的产物,是为防止各运输方式间过度竞争、某种运输方式的垄断、避免重复建设和不合理利用导致运输资源的巨大浪费,而发展起来的概念。在构建综合运输体系的背景下,公路网布局规划有了以下的改变:
(1)与其他运输方式的线路和场站紧密衔接,起到集散客流,服务货运的重要作用;
(2)线路等级级配合理,网络可达性佳,充分发挥公路运输机动灵活的优势。
为适应构建综合运输体系背景下公路网布局的变化,本文采用基于节点布局法,通过公路网路线重要度密度得到基础网络布局,以路网可达性边际效益最优为目标,得到城市公路网络布局。
2.1 节点的选取
节点指一个区域交通需求的代表点,相应区域的经济、人口、交通都集中在节点上,故节点也是路网规划中需要连接的点。首先对规划区域进行调查,调查内容包括该地区的经济、人口、资源和交通情况,以确定哪些地点作为路网规划的节点[5]。节点选取是城市公路网布局的第一步,节点选取的正确与否直接影响城市公路网布局方案。节点选取过粗,会造成局部区域的可达性差,无法实现公路运输“门到门”的服务特点;节点选取过细,会使研究工作过于繁杂。城市公路网规划应以区域内的片区(组团)、重要综合交通枢纽、主要产业园区为节点,尽量符合行政区范围,以减少资料调查整理的难度。
2.2 公路网布局方案初拟
在对城市经济现状、交通现状以及城市的发展思路与规划进行充分调研的基础上,分析现状路网与发展需要的差距,同时考虑构建综合运输体系的要求,按照以下三种承担不同功能的公路类型来进行城市公路网络布局方案的初拟。
(1)通达路
承担主要的过境交通和城市对外交通,提升城市的交通区位和投资环境,带动城市的发展。
(2)通道路
城市各片区之间的通道,加强各片区之间的联系,产生整个城市经济发展的内聚效应。
(3)联网路
衔接其他运输方式的线路和场站,形成协调发展的综合运输网络。
2.3 重要度分析
2.3.1 节点重要度分析
节点重要度是判断路网节点重要程度的指标,可选取人口、地区生产总值、工业产值、运输量、商品零售总额等指标进行定量化分析,计算模型如下:
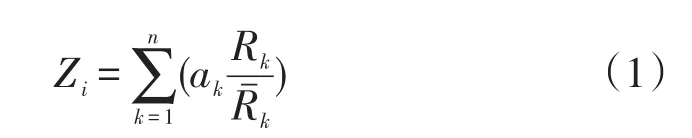
式中:Zi为节点i的重要度;ak为第k项指标的权重,通过主成分分析法确定;Rk为本节点的第k项指标值;Rˉk为规划区域所有节点的第k项指标平均值;n为选取的指标个数。
2.3.2 路线重要度分析
路线构成路网中两个节点之间连通路径,路线重要度受到其连接的节点重要度、地理位置等因素的影响,本文定义路线重要度为:

式中:LZa为节点i, j之间路线a的重要度;Zi,Zj为节点i, j的重要度; f(Rij)为节点i, j之间的交通阻抗,Rij与距离、时间有关。
2.4 公路网重要度密度最优树求解
定义路线重要度密度为路线重要度与其长度的比值,即:
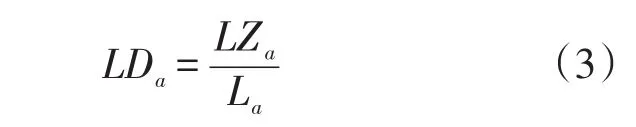
式中:LDa为路线a的重要度密度;LZa为路线a的重要度;La为路线a的长度。
以路线重要度密度作为各路线的权重,通过Kruskal算法求解公路网路线重要度密度最优树。Kruskal算法的基本思想为:假设有N个节点,选择无向加权连通图中权值最小且不和已选择的边形成圈的边,并将其添加到边集E中;否则就选择下一条边,直到边集E中有N-1条边为止[7]。而以路线重要度密度为权值的公路网络布局规划选择权值最大为最优树的边,因此,公路网络重要度密度最优树的求解步骤为:
(1)初始化节点集A={φ},边集E={φ},所有边的权值的和WT=0;
(2)将所有的边按路线重要度密度权值按从大到小的顺序排列,记为E′;
(3)选择在边集E′中重要度密度权值最大的,且不和边集E中的边构成圈的边eij,若其满足 WT+LDij≤WT+LD′ij(eij是连接节点i和 j的边,LDij是边eij的路线重要度密度权值,LD′是没有被选择边中的任意一边的路线重要度密度权值),则将节点i和 j中没有在点集A中的点添加到A中,并将边eij添加到边集E中;否则不选择这条边;
(4)重复第3步直到节点集有N个顶点,边集中有N-1条边,即可得到公路网络密度最优树的布局。
2.5 基于可达性的公路网络布局完善
2.5.1 可达性分析
网络可达性能够反映公路网络中各节点间交通的便捷程度,是表示公路网特性的一个重要指标,通常由节点可达性来表征。节点可达性主要反映公路网中某一节点与其他各节点间的相互关系,反映该节点对外交通联系的便捷程度,体现该节点在路网中的地位。节点之间不同的路线等级和连接方式都将使便捷程度(即可达性)有所变化,因此节点可达性可作为判断方案优劣性的依据[8]。
(1)节点可达性分析
从节点可达性的定义上来看,节点之间的路线等级以及路线的连接方式是影响可达性的两个方面。在路线的连接方式上,两个节点之间可以直接连接,也可以通过其他节点迂回建立起连接,节点之间的实际里程越大,可达性就越小。因此,用两个节点之间的实际里程与直接相连时的里程的比值来反映可达性;在路线等级上,不同的路线等级决定了车辆的行程时间,在节点交通需求及路线长度一定的情况下,路线等级越高,服务质量和服务水平越好,车辆的行程时间越少,可达性就越大。综上所述,节点可达性模型为:

式中:Ai为节点i的可达性;Lij为节点i,j之间的公路线路长度;LA为公路网的总里程长度;Rij为节点i,j之间的交通阻抗。
(2)公路网络可达性分析
考虑节点重要程度不同,以节点重要度为权重,将公路网中所有节点的可达性的加权求和值作为公路网络的可达性,即:
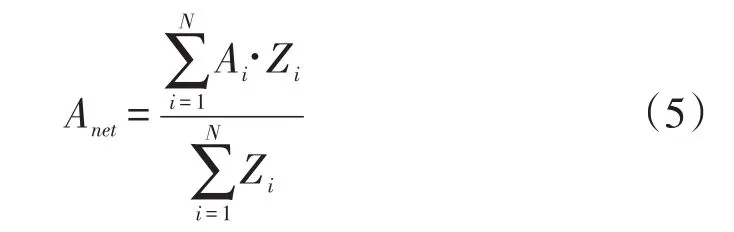
式中:Anet为公路网络可达性;Ai为节点i的可达性;Zi为节点i的重要度。
上述模型中,Anet数值越大,可达性越差。
2.5.2 公路网络布局的完善
前面求解出来路线重要度密度最优树,记其线路集为E,对应的网络可达性为,以其作为城市公路网络布局的基础边,与初拟的公路网络布局方案(记其线路集为G)进行比较,得出未纳入最优树的线路集(G-E)。对于这些线路,按照通达路、通道路和联网路三个层次,以路线重要度密度为标准由大到小进行排序,记此序列为r(k),逐一将其纳入到公路网络布局方案中,每纳入一条新的线路,计算路网可达性,记为,若<,则将该线路纳入到线路集E中,升级一次路网布局,重新计算线路集E中对应的网络可达性;否则不选择该线路,直至序列r(k)序完结。
随着路网规模的增加,路网可达性的值总是在减小,但是减小的幅度越来越小,因此,选择可达性数值降低幅度开始不显著的线路集E作为城市公路网最佳布局。在此过程中,还应以根据社会经济发展状况和运输量的变化特征预测得到的公路网建设总规模为约束条件。
3 案例应用分析
将本文提出的布局方法应用于太仓市城镇快速通道体系规划中。
3.1 节点选择与重要度计算
分两个层次选择节点,第一个层次节点为乡镇所在地,第二个层次为行政村。本文主要针对第一层次进行分析。太仓市快速通道体系中第一层次节点为城厢镇、沙溪镇、璜泾镇、浏河镇、浮桥镇、陆渡镇和双凤镇。节点重要度如表1所示。

表1 节点重要度计算表
3.2 方案初拟
通过对太仓市城市经济现状、交通现状以及城市的发展思路与规划充分调查分析的基础上,得出现状的城镇快速通道体系与发展所需的差距,初步拟定太仓市城镇快速通道体系的布局方案如图1所示。
3.3 线路重要度密度最优树及可达性计算
计算各线路的重要度及重要度密度,运用Kruskal算法求解得到线路重要度密度最优树,如图2所示,此时布局方案的路网可达性为72.7,各节点的可达性如表2所示。

图1 布局方案初拟图
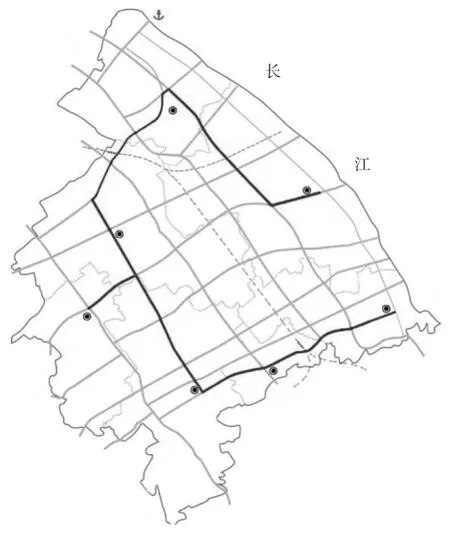
图2 线路密度重要度最优树
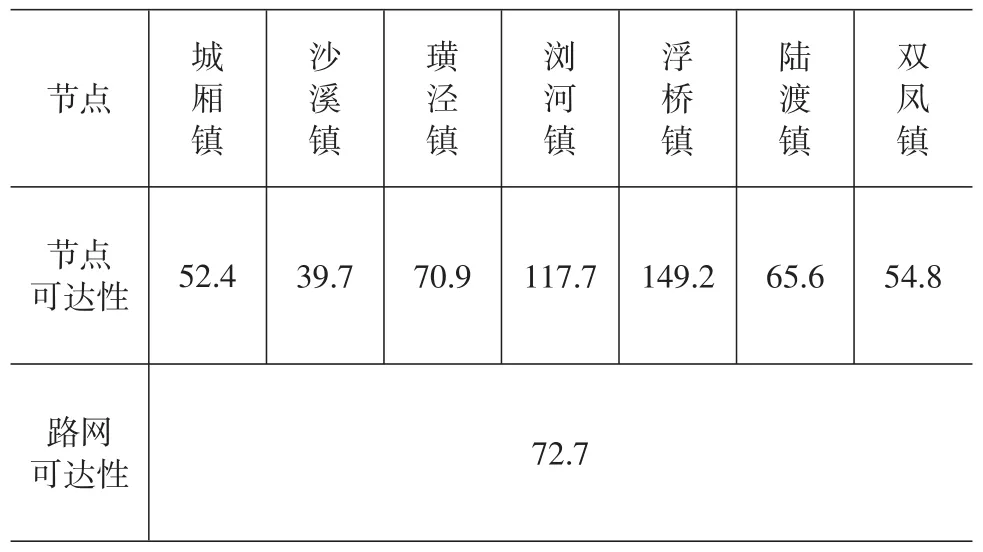
表2 最优树可达性计算表
3.4 布局完善
将最优树之外的线路按照线路重要度密度大小顺序排列,依次列入到快速通道体系布局方案中,重新计算各节点可达性和路网可达性,如果路网可达性值减小,则将该线路纳入到城镇快速通道体系中,否则更换下一条线路,直到完结。最终得到太仓市城镇快速通道布局方案如图3所示,各节点可达性和路网可达性如表3所示。
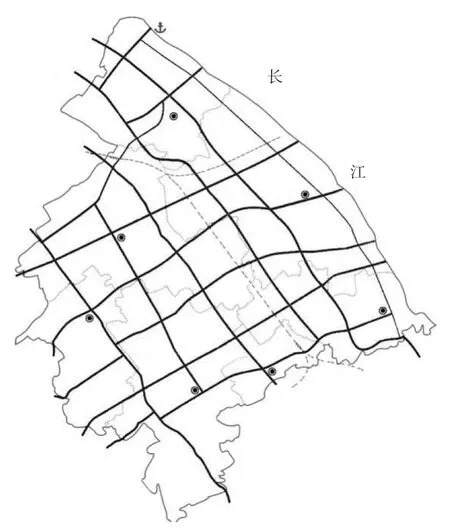
图3 太仓城镇快速通道体系布局图
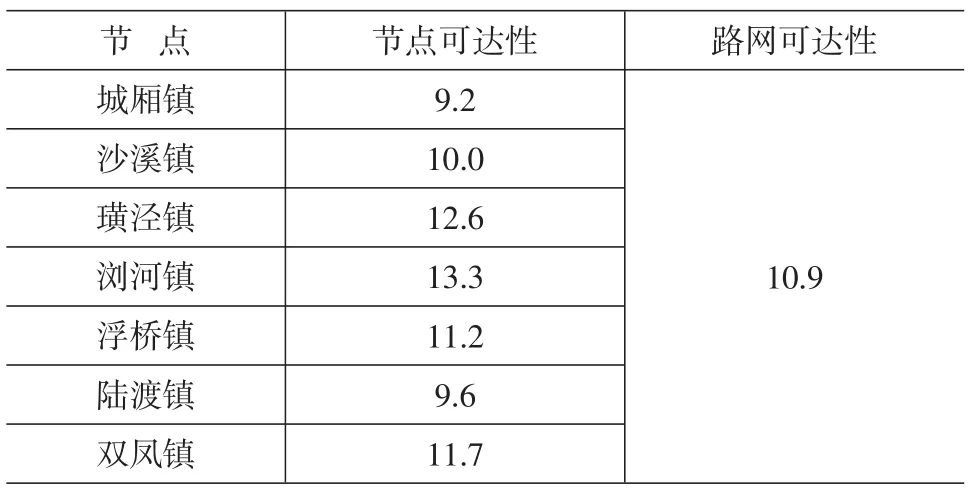
表3 布局方案可达性计算表
4 结语
本文在分析构建综合运输体系背景下公路网布局的新思想的基础上,通过求解公路网路线重要度密度最优树得到基础网络布局,再以路网可达性边际效益最优为目标,得到城市公路网络最佳布局。本文所示方法在太仓市城镇快速通道体系规划中的应用表明此方法具有较好的操作性和实用性。
[1]刘洪,王元庆,张鹤.综合运输体系形成期高速公路布局方法探讨[J].交通科技,2010(2):84-86.
[2]中华人民共和国交通运输部,公路网规划编制方法[Z].北京:中华人民共和国交通运输部,2010.
[3]邝青梅.经济发达地区市域公路网布局规划与评价研究[D].哈尔滨:哈尔滨工业大学,2006.
[4]石兆旭.区域公路网布局形态及发展规模研究[D].北京:北京工业大学,2006.
[5]王保华.综合运输体系下快捷货物运输网络资源配置优化研究[D].北京:北京交通大学,2010.
[6]过秀成,胡斌,陈凤军.农村公路网规划布局设计方法探讨[J].公路交通科技,2002,19(2):92-95.
[7]王伟,孟思燕.kruskal算法的研究与改进[J].重庆文理学院学报:自然科学版,2010,29(3):25-27.
[8]盖春英,裴玉龙.公路网络可达性研究[J].公路交通科技,2006,23(6):104-107.
