海洋二号卫星散射计风场产品真实性检验及分析

王东良，姚小海，孟雷，张维凯

（5111信箱，北京 100094）

1 引言

海面风场是海洋环境一个重要参量，不仅可以直接生成海浪，还可以决定海表上空的水汽和温度，进而影响大气与海洋之间的能量交换，对洋流、海洋气象和气候环境的分析与预测起到至关重要的作用[1]。遗憾的是海面风场资料严重缺乏，从浮标和船舶所获得的风测量数据十分有限，且离散性大，分布不均匀。卫星遥感技术的发展很好的解决了这一难题，卫星观测的风场具有覆盖范围大、时空分辨率高、数据资料获取容易等优点。其中,微波散射计就是一种重要的遥感手段,它可以全天候地测量海面风速和风向。

微波散射计通过测量风引起的粗糙海面对微波的后向散射特性来推算海面风场。在海面上，毛细波叠加在重力波上，风的变化引起海表面粗糙度的变化，散射计接收到的后向散射会随之变化。根据后向散射与风矢量之间的相关模式，经过地球物理定标后就能得出海面风场[2]。

随着散射计产品重要性不断提高，应用领域不断扩大，有必要对产品的真实性进行检验，以保证数据产品的可靠性和促进反演算法的改进。国际上已有部分学者开展了相关工作：Freilich和Dunbar（1999)利用NDBC浮标数据验证NSCAT散射计的风速、风向反演精度，在剔除了超过3个标准偏差的风速数据后，NSCAT散射计数据的均方根误差为1.2 m/s，均值偏差为0.3 m/s，当风速为2—17 m/s并忽略了风向的多解，风向的均值偏差为8°，均方根误差为 18°[1-3]；Dudley Chelton（2003）指出SeaWinds散射计与NSCAT相比具有类似的风矢量反演精度[4]；Nanto对比QuickSCAT散射计资料和全球浮标、船舶报资料，得到两者风速的均方根误差为1.01 m/s，风向均方根误差为23°[5]。

海洋二号（HY-2）卫星是我国第一颗动力环境卫星，该卫星集主、被动微波遥感器于一体，能获取包括海面风场、浪高、海流、海面温度等多种海洋动力环境参数。张婷等（2013）利用南海北部石油平台的气象测风仪对ASCAT和海洋二号散射计所测风场数据进行了对比分析：海洋二号散射计所测风速和石油平台气象站观测风速的均方根误差为3.41 m/s，风向的均方根误差为58.66°；在150 min和15 km的时空窗口下，ASCAT与海洋二号风速的均方根误差为0.72 m/s，风向的均方根误差为8.50°[6]。本文利用国际海—气综合数据集（ICOADS）的海面风场实测数据作为真实值对2012年5月—2013年5月的海洋二号散射计风场产品进行真实性检验。对比之前先根据卫星产品的空间分辨率和海面风场的时空变化规律对数据进行时空匹配，提取满足相应时空条件的配对样本数据，再对两者的风速、风向进行对比，计算平均误差、平均绝对误差、均方根误差等误差统计量，以此对海洋二号散射计风场产品的精度进行评估。

受散射计海面风场反演原理的限制，海洋二号散射计在2—24 m/s风速范围内的风场产品较为可靠。本文将先对海洋二号散射计风场产品在全风速条件下进行整体评估检验，再对2—24 m/s风速范围内风场产品按各风级划分进行具体统计检验。

2 数据说明及检验方法

2.1 数据说明

国际海—气综合数据集，简称ICOADS，是美国NOAA气候诊断中心的研究成果。它收集了1800年至近期的世界海洋表层观测资料，包括来自船舶的测量或观测数据、系泊浮标和漂浮浮标数据、海岸站点数据以及其他海洋台站数据，是目前最完整和最多样化的海—气综合数据集。数据集的主要变量有海表温度、气温、风场、气压、云量等气象、海洋要素，每个变量都分为“standard”和“enhanced”两部分数据，反映的是质量控制、混合数据的差异。"standard"资料用其气候数据的3.5σ（标准差）进行限制校订，观测数据仅限于船舶观测。“enhanced”资料则使用范围更广泛的4.5σ（标准差）进行校订，以更好地描述极端气候事件，它使用了船测和其他海上平台原位观测（现场观测）类型数据。本文采用“enhanced”资料。

海洋二号卫星散射计刈幅优于1700 km，每天覆盖全球海洋80%以上。本文采用海洋二号卫星散射计二级产品中的海面风场数据，空间分辨率为25 km。资料的时间范围为2012年5月25日—2013年5月31日，其中2013年3月、4月有部分日期产品资料缺失。

2.2 时空匹配

卫星产品和现场实测数据具有不同的时空采样特性。为了确保卫星观测时间、采样区域和实测观测站点测量时间、位置的一致性，本文采取严格的控制标准，根据卫星产品的空间分辨率和海面风场的时空变化规律确定合理的时空匹配窗口。依据该窗口，将海洋二号散射计海面风场资料与ICOADS实测资料进行匹配，作为后续检验的数据集[8]。综合考虑，本文采取的时间匹配窗口为10 min，空间匹配窗口为12.5 km，即当散射计测量时间与实测站点观测时间≤10 min，空间距离≤12.5 km时，就认为两者测量结果为同步观测。

采用上述时空匹配方法，我们共获得了37175个配对样本。在2—24 m/s风速范围内共有36150个配对样本，约占样本总数的98.81%。统计发现：配对样本主要集中在0—16 m/s风速范围内，风速大于16 m/s的样本个数明显偏少；在各风向上的配对样本个数大体一致。

值得注意的是，ICOADS数据观测点主要集中在北半球，加上时空匹配条件的限制（见图1），本文得到的结论有一定的局限性，为得到更全面的分析有待于数据的进一步积累。

2.3 统计检验方法

本文主要误差统计量计算公式为：

式中，H为海洋二号散射计风场产品的风速或风向值，I为ICOADS实测的风速或风向值，n为相应样本个数。

图1 满足时空匹配窗口的ICOADS观测站点分布图

3 真实性检验及分析

3.1 风速的真实性检验

3.1.1 全风速条件下风速真实性检验

首先计算各样本ICOADS实测风速与海洋二号散射计风速误差，以2 m/s间隔分类（如-1—1 m/s），观察配对样本在各风速误差区间内的统计分布特征。

从图2可知，海洋二号散射计风速与ICOADS实测风速的误差接近以0 m/s为轴成对称分布；两者风速误差主要集中在-1—1 m/s范围内，约占总样本数的49.2%，在-3—3 m/s误差范围内的样本数占总数的86.6%，当两者风速误差超过±3 m/s，样本数急剧减少。

将ICOADS的实测风速以1 m/s的间隔分类，分别计算ICOADS和与之配对的海洋二号散射计在各风速区间内风速值的平均，绘制ICOADS实测风速和海洋二号散射计风速比较图（见图3）。

图3中，上三角表示超过500个风速样本的平均，下三角表示0—500个风速样本的平均，点线表示1∶1的理想状态，实线表示平均风速线性拟合，图3b为根据莱茵达准则，剔除超过3个标准偏差的风速样本（剔除样本约占样本总数的5.24%）后的风速比较图，其线性拟合的线性回归方程为VICOADS=0.8595VHY-2+1.1671。

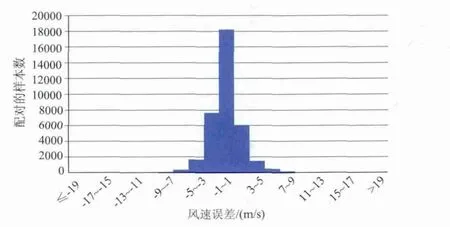
图2 ICOADS和海洋二号散射计各风速误差范围内配对样本个数分布图

从图3中可以看出，海洋二号散射计风场产品的风速在4—15 m/s范围内反演的效果较好。在较低风速和高风速情况下，海洋二号散射计风速与ICOADS实测风速误差相对较大。在较低风速情况下，由于此时的后向散射主要由小振幅波决定的，因此散射计的风速测量误差较大，其次海流也会影响散射计的测风精度；在高风速情况下，船舶和浮标会发生倾斜，海浪的飞沫和海面高度的变化也会影响风速的测量精度[1-9]，另外，高风速条件下的配对样本数偏少，统计特征代表性相对较差，也可能是引起两者风速误差较大的原因。剔除超过3个标准偏差的风速数据后，海洋二号散射计风速在高风速段的拟合效果明显改善，也间接说明了海洋二号散射计风场产品在高风速情况下风速反演存在较大误差。根据殷晓斌（2007）的发现，当风速大于20 m/s的情况下，散射计严重地低估了实际的海面风速，需使用卫星云图和角动量守恒公式进行修正[10]。

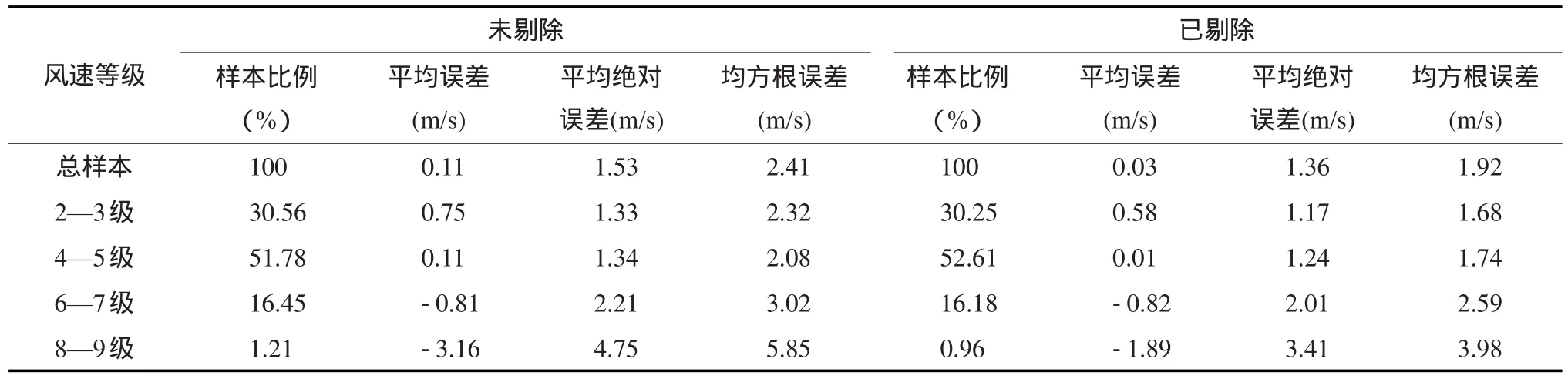
表1 各风级范围内海洋二号散射计风速与ICOADS实测风速误差统计特征量

对比点线和实线可以看出，在0—9 m/s风速范围内，海洋二号散射计风速略大于ICOADS实测风速；当大于9 m/s时，海洋二号散射计风速要略小于ICOADS实测风速。

海洋二号散射计风速与ICOADS实测风速的均方根误差为2.44 m/s，风速平均误差为0.17 m/s，平均绝对值误差为1.55 m/s；剔除了超过3个标准偏差的风速样本后，海洋二号散射计风速与ICOADS实测风速的均方根误差为1.95 m/s，风速平均误差为0.08 m/s，平均绝对值误差为1.39 m/s。

对于风速的检验，因散射计测量的风速是10 m风速，为中性稳定风速，与实测风速略有不同。另外表层边界层的层化状态也会影响散射计的测量：不稳定层化会使散射计反演的风速较实测值偏大，而稳定层化会使散射计反演的风速比实测值偏小，误差范围在0.1—0.2 m/s[2-9]。

3.1.2 2—24 m/s范围内风速真实性检验

为更好检验海洋二号散射计在不同风速条件下反演效果，根据日常业务保障中的使用习惯，将配对样本按照蒲福风力表的风级划分为四类，即划分为2—3级、4—5级、6—7级和8—9级四类。统计发现：配对样本主要集中在中、低风速区（2—5级），强风速区的配对样本数偏少，风速≥8级的样本仅占1.21%；

下面分别针对未剔除超过3个标准偏差风速样本和已剔除超过3个标准偏差风速样本（剔除样本约占样本总数的5.35%）两种不同情况计算各风级范围内样本的风速误差统计特征量，具体结果见表1。

从表1可以看出，剔除超过3个标准偏差风速样本后海洋二号散射计与ICOADS两者各风速误差统计特征量都明显变小。对于剔除前的样本，海洋二号散射计与ICOADS两者风速的平均误差为0.11 m/s，海洋二号散射计风速要略高于ICOADS实测风速；在低风速条件下，两者风速平均误差为0.75 m/s，随着风速增加，两者平均误差逐渐减小，随着风速再次增加，海洋二号散射计风速将低于ICOADS实测风速，两者平均误差逐渐增大；当风速≥8级，两者平均误差达到最大，为-3.16 m/s，海洋二号散射计严重低估了实际海面风速。海洋二号散射计与ICOADS两者风速的平均绝对误差和均方根误差基本随着风速的增大而增大。对于剔除后的配对样本，其各风速误差统计特征量的变化趋势与剔除前样本大体一致。

通过对比分析可知，在中、低等风速条件下海洋二号散射计风速与ICOADS实测风速具有较好的一致性，但在较高风速条件下海洋二号散射计会出现风速低估现象。总的来说，在2—24 m/s风速范围内海洋二号散射计风速的反演精度要略优于全风速条件下的反演精度。

3.2 风向的真实性检验

3.2.1 全风速条件下风向真实性检验

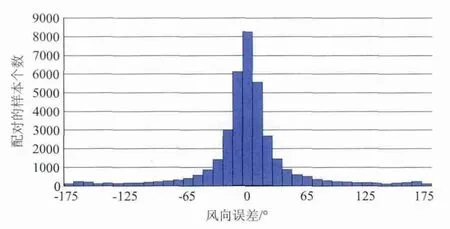
图4 ICOADS与海洋二号散射计各风向误差范围内配对样本个数分布图

首先将海洋二号散射计与ICOADS的风向误差以10°间隔分类（如-5°—5°），观察配对的样本个数在各风向误差范围内的统计分布特征。

从图4可知，海洋二号散射计与ICOADS的风向误差主要集中在-15°—15°范围内，约占样本总数的53.5%。两者风向误差接近以0°为轴成对称分布，随着两者风向误差的增大，样本数急剧减少，但在风向误差超过155°后出现了较小的峰值。

Freilich和Dunbar将风向差超过60°定义为风向多解[2-3]。根据此定义，我们共找到了5242个风向多解样本，约占总样本数的14.1%。单独对风向多解样本进行统计分析，如图5所示，我们发现：风向多解主要发生在低风速区，这主要是由于在低风速时，浮标和散射计的测量的风向精度都偏低[3-9]，随着风速的逐渐增大，风向多解发生概率逐渐降低，但在高风速区出现了小的波峰；在各风向上风向多解发生概率虽有小幅震荡，但基本保持一致，维持在0.14左右。

海洋二号散射计与ICOADS两者风向的均方根误差为48.90°，平均绝对误差为29.11°；若忽略风向多解的影响，海洋二号散射计与ICOADS两者风向的均方根误差为20.51°，平均绝对误差为15.20°。

3.2.2 2—24 m/s范围内风向真实性检验

对于海洋二号散射计风向的真实性检验，也依照其风速真实性检验的划分方法,将配对样本按风级划分为四类，分别针对未剔除风向多解样本和已剔除风速多解样本（剔除样本约占样本总数的13.13%）两种不同情况计算各风级范围内样本风向的误差统计特征量，因平均误差不适用于风向的误差统计分析，故在此不做计算，具体结果见表2。

图5 风向多解样本统计分布

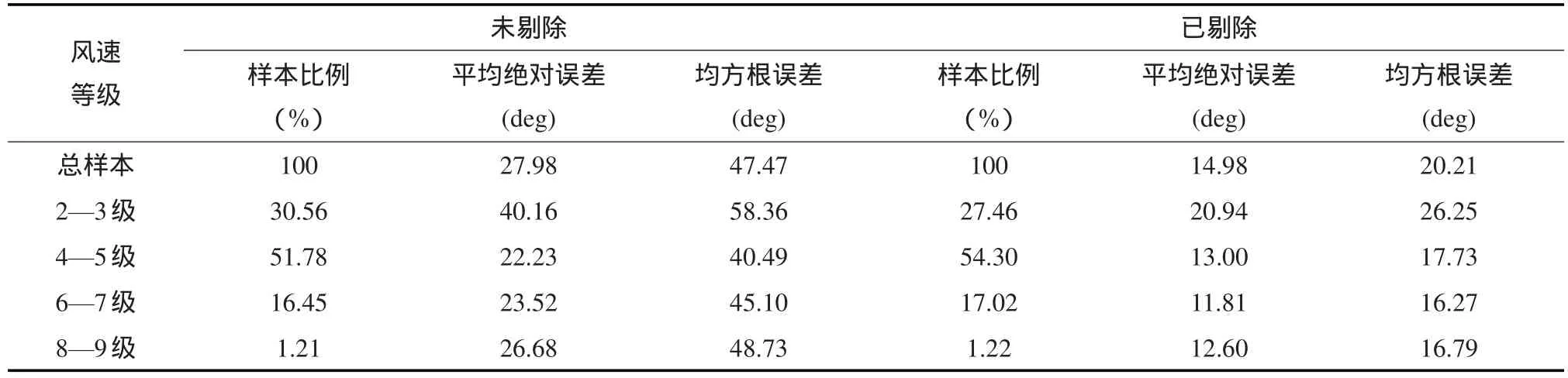
表2 各风级范围内海洋二号散射计风向与ICOADS实测风向误差统计特征量

从表2可以看出，剔除风向多解样本后，海洋二号散射计与ICOADS两者风向误差统计特征量明显变小。对于未剔除风向多解的配对样本，海洋二号散射计与ICOADS两者风向的平均绝对误差为27.98°，均方根误差为47.47°，在低风速条件（2—3级）下，两者风向误差统计特征量最大，平均绝对误差达到40.16°均方根误差达到58.36°；随着风速的增大，到中等风速时，两者风向误差统计特征量最小；随着风速的再次增大，两者风向误差又呈现逐渐增大趋势，但增幅相对较小。对于已剔除风向多解的配对样本，海洋二号散射计与ICOADS两者风向的平均绝对误差为14.98°，均方根误差为20.21°，两者风向误差统计特征量的最大值同样出现在低风速条件（2—3级）下，平均绝对误差为20.94°，均方根误差为26.25°；在其他风级区，两者风向误差统计特征量都远小于低风速条件下的误差统计特征量，各风级区之间样本的风向误差统计特征量相差不大。

总的来说，在低风速条件下，海洋二号与ICOADS两者风向存在较大偏差，而在其他风速条件下，两者的风向误差统计特征量较为接近，都远小于低风速条件下的误差统计特征量。

4 小结

本文基于国际海—气综合数据集（ICOADS）的实测风场数据，对海洋二号散射计风场产品进行了真实性检验及分析，初步得到以下结论：

（1）海洋二号散射计风速与ICOADS实测风速数据具有良好相关性，在中、低风速条件下，两者风速具有较好的一致性，但在较高风速条件下海洋二号散射计会出现风速低估现象；

（2）在2—24 m/s风速范围内，海洋二号散射计与ICOADS两者风速的平均绝对误差为1.53 m/s，均方根误差为2.41 m/s，剔除超过3个标准偏差风速样本后，两者风速的平均绝对误差为1.36 m/s，均方根误差为1.92 m/s；

（3）海洋二号散射计风向与ICOADS实测风向的误差主要集中在-15°—15°范围内，在低风速条件下，海洋二号与ICOADS两者风向存在较大偏差，风向多解也主要发生在低风速情况下，在各风向上风向多解发生概率基本一致，约为0.14；

（4）在2—24 m/s风速范围内，海洋二号散射计与ICOADS两者风向的平均绝对误差为27.98°，均方根误差为47.47°，若忽略风向多解的影响，两者风向的平均绝对误差为14.98°，均方根误差为20.21°。

[1]苗俊刚,刘大伟.微波遥感导论[M].北京:机械工业出版社,2012.

[2]冯士筰,李风岐,李少箐.海洋科学导论[M].北京:高等教育出版社,1999.

[3]Freilich M H,Dunbar R S.The accuracy of the NSCAT 1 vector winds:comparison with National Data Center buoys[J].J Geophys Res,104(C5):11231-11246.

[4]Chelton D B,Freilich M H.Scatterometer-based assessment of 10-windsanalysesfrom theoperationalECMWF andNCEP numerical weather prediction models[J].Monthly Weather Review,2005,133(2):409-427.

[5]Naoto E,Hans C B,Michael J C.Evaluation of wind vectors observed by QuickSCAT/Sea Winds using ocean data[J].Journal of Atmospheric and Oceanic Technology,2002,19(12):2049-2062.

[6]张婷,张杰,杨俊钢.卫星散射计与海面平台所测的风场数据比较[J].海洋学研究,2013,31(2):45-51.

[7]穆松宁.海-陆-气常规数据说明手册（2011版）[R].中国科学院大气物理研究所,2011:73-74.

[8]孟雷,何宜军,伍玉梅.基于SSMI数据的神经网络方法反演海面风速[J].高技术通讯,2006,16(7):763-770.

[9]Seelye Martin.海洋遥感导论[M].蒋兴伟等译,北京:海洋出版社,2008.

[10]殷晓斌,王震占.微波传感器遥感台风对海洋影响的初步分析[R].2007年全国微波毫米波会议论文集（下册）,2007,2:1739-1742.