利用风暴潮数值模式计算重现期风暴潮的一种方法

张百超，董剑希，吴少华

（1.南京信息工程大学，江苏南京 210044；2.国家海洋环境预报中心,北京 100081）

1 引言

随着计算机和计算技术的飞速发展，风暴潮数值模式在实时预报和海洋工程数值计算中发挥了越来越大的作用。例如，美国的SLOSH（Sea,Lake,&Overland Surges from Hurricanes）模式[1]，能预报海上、陆上以及湖上的台风风暴潮，在防灾预报中发挥了很好的作用。英国的自动化温带风暴潮预报模式“海模式”（Sea Model），气压场和风应力场采用10层大气模式提供的预报结果，进行温带风暴潮预报，取得很好的效果。20世纪80年代，我国风暴潮的数值模式研究得到了相当迅速的发展。现已对渤海、黄海、东海和南海陆架区的风暴潮进行了相当数量的数值模拟实验，并以此来研究各动力因子的效应，渤海还采用了超浅海风暴潮三维模式进行数值实验[2-3]。模式实验获得了许多有意义的结果。有的模式已经在实时预报中使用[4]，有的模式在GIS支持下能计算局部地区的风暴潮漫滩[5]，在风暴潮的防灾减灾中发挥了重要的作用。

近年来，随着沿海经济的迅猛发展，需建设大量的沿岸海洋工程，如核（火）电厂、海堤、港口、大型工厂等。而这些沿岸海洋工程的建设经常需要计算重现期风暴潮。通常的计算方法需要工程点数十年的潮位观测资料进行统计计算，如果工程点没有长时间序列潮位观测资料，则需要工程点与附近具有数十年观测资料的海洋观测站的同步观测资料进行相关订正后计算。如何解决观测数据不足这个科学问题？葛黎丽[6]等利用数值模拟和资料同化技术进行南海30年重现期分析。于宜法[7]赵滨[8]等学者利用风暴潮数值计算方法进行了重现期研究，取得较好的研究成果。本文在前人研究的基础上，进一步条理化基于风暴潮数值计算模式的重现期分析的工程解决方案，利用验证的风暴潮数值模式计算出工程点每年最大的风暴潮序列，然后利用该序列进行重现期风暴潮的统计计算。本文以广东阳江市沙环站为例，计算了沙环站的重现期风暴潮，并与通常的方法进行了比较，计算结果表明，此方法与通常的方法相比，精度相当，对于无长时间序列验潮资料的工程点，特别对于附近也无长时间序列验潮资料的工程点的重现期风暴潮计算，具有很大的参考价值。

2 风暴潮数值模型及其检验

2.1 风暴潮数学模型

在球坐标系下，控制风暴潮运动的深度平均流方程可以写成如下形式：

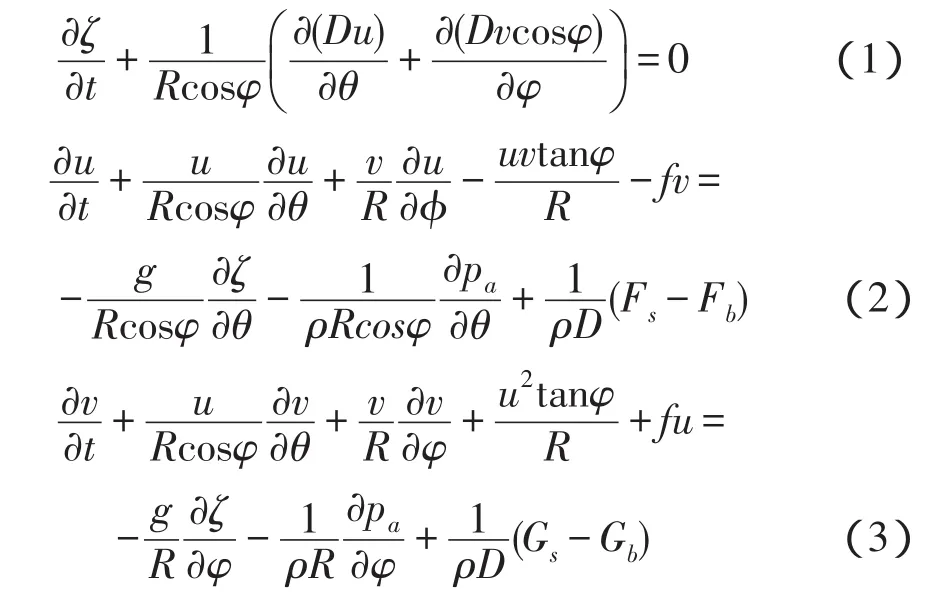
式中，t代表时间，θ,φ分别代表经度和纬度，z代表从平均海平面起算的水位高度，u,v代表深度平均流的经向和纬向分量，Fs,Gs代表海表面风应力τs的经向和纬向分量，Fb,Gb代表海底摩擦应力τb的经向纬向分量，Pa代表海表面的大气压力，D代表总水深，ρ代表海水密度，假定为均匀的，R代表地球半径，g代表重力加速度，f代表Coriolis参数(f=2ωsinϕ）。

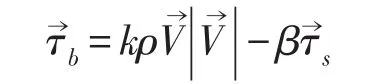
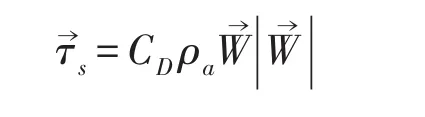
式中，ρa是空气密度，CD是风曳力系数。计算时取k=CD=2.6×10-3，β=0.35。

2.2 台风域中气压场和风场的计算

2.2.1 气压场的计算

（1）Takahashi,1939：

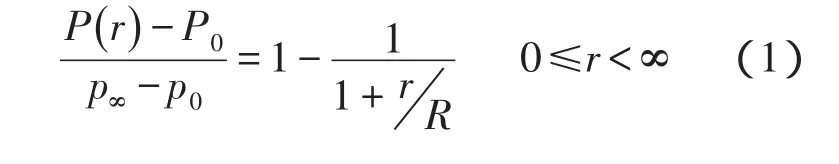
（2）Fujita.T.,1952：

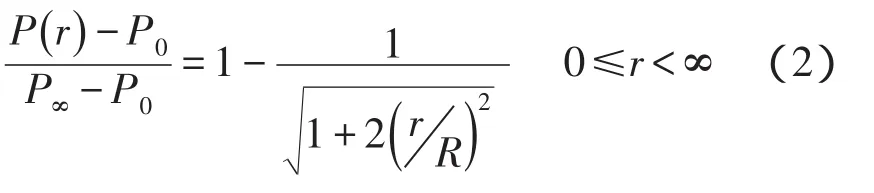
式中，P∞为台风外围气压（正常气压），P0为台风中心气压，R为台风最大风速半径，P()r为距台风中心r距离处的气压。在0＜r＜2R范围内，式（2）能更好地反映台风的气压变化；在2R≤r＜∞的范围内，式（1）有更好的代表性。因此,选用式（1）、（2）嵌套来计算同一台风域中的气压场分布。

2.2.2 台风风场的计算

台风域中的风场由两个矢量场叠加而成。其一是相对台风中心对称的风场，其风矢量穿过等压线指向左方,偏角（流入角）为20度，风速与梯度风成比例；其二是基本风场，假定其速度（）取决于台风移速。这里用Veno Takeo(1981）的公式表示：

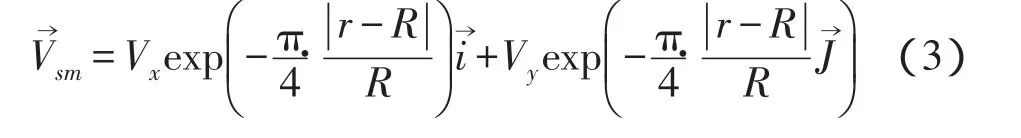
式中，Vx,Vy为台风移速在x,y方向的分量。

2.3 数值模式的计算方法

2.3.1 差分方法

模式采用有限差分方法求解方程，网格为Arakawa C型网格，采用前差－后差（一种半隐式差分格式）差分格式求解2.1中的方程（1）、（2）、（3），为了使模式的稳定性增强，摩擦项采用隐式。

2.3.2 嵌套网格的设计与处理:

众所周知，要想提高风暴潮数值模式的计算精度，计算区域必须足够大，最好能与台风的尺度同样大，这样水边界的计算就非常准确。但是，当风暴潮传播到浅水区域，例如，陆架区、河口区、小海湾等区域，海岸形状和海水深度对风暴潮的影响是非常重要的，所以需要精细的网格来刻画。基于以上的考虑，我们采用计算区域加大，重点区域加细的思想来设计模式的网格分布。因此，设计了三重网格系统用于计算沙环的风暴潮。如表1所示，整个计算区域分为三个子区域，每个区域采用不同的时间步长和空间步长。

第一套网格（粗网格）的初始条件为：

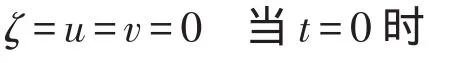
海岸边界条件为:Vn=0

表1 风暴潮数值模式的格点系统配置

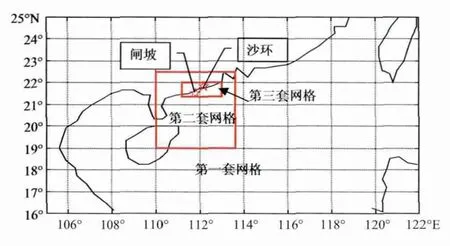
图1 风暴潮模式三套网格相对位置图

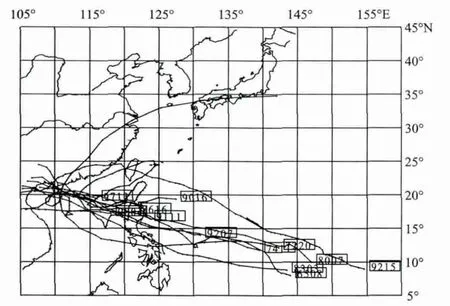
图2 12个模拟台风路径图

式中，Vn为岸边界的法向深度平均流流速。水边界取为静压边界条件:

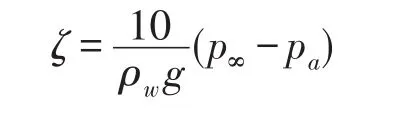
式中，z是以海平面起算的水位高度（m），ρw是海水密度，p∞=1008 hPa是外围气压。

3 数值模型模拟检验

采用建立的数值模型对登陆华南沿海的12次有代表性的台风风暴潮过程进行了模拟计算。这些台风是：6508号台风（Freda），7220号台风（Pamela），7411号台风（Ivy），8007号台风（Joe），8303号台风（Vera），8616号台风（Wayne），9004号台风（Nathan），9016号台风（Becky），9111号台风（Fred），9207号台风（Cary），9215号台风（Cary），9713号台风（Tita）。图2给出了上述12次台风移动路径（6 h间隔）。

表2给出了12次有代表性的台风风暴潮过程计算值与实测值的比较。从图3中和表2中可以看出，尽管模拟的全过程与实况比较不全尽人意，但就过程最大增减水值而言，不论从两者位相差和量值差来考察，都表明：所建立的风暴潮模式，以及计算气压场与计算风场均满足计算要求。

4 数值方法计算沙环不同重现期风暴潮位

根据对沙环有影响的历史台风资料，选择历年能使沙环验潮站产生较大增水的台风（热带气旋），利用上述验证的风暴潮数值模式对沙环站进行风暴潮数值计算，计算中最大程度地使闸坡的计算结果准确。然后从沙环的数值计算结果中挑出每年的最大增水值构成最大增水系列进行频率（随机法）计算（样本见表3），利用统计法求得沙环重现期风暴潮。

根据沙环验潮站的数值模拟台风增水年极值系列（样本见表3），采用龚贝尔（Gumbel）方法计算的重现期风暴潮，如表4所示。

根据沙环验潮站的数值模拟台风增水年极值系列（样本见表3），采用皮III型计算沙环站重现期风暴潮，见表5，Cv=0.433,（Cs/Cv）4。

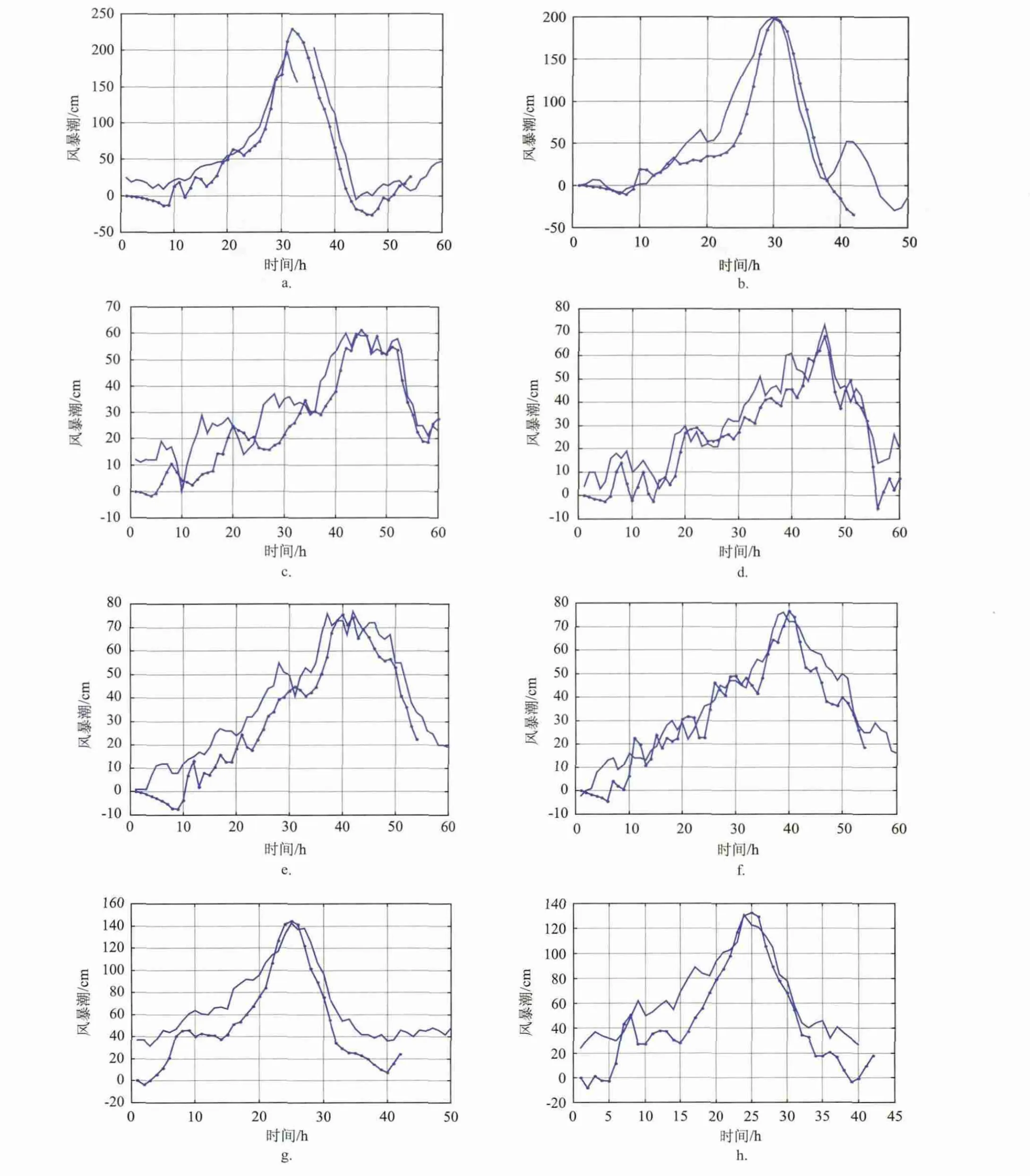
图3 a、b、c、e、f分别是6508、8007、9004、9016、9713号台风期间闸坡站风暴潮计算值与观测值比较，d、g、h分别是9004、9016、9713号台风期间沙环站风暴潮计算值与观测值比较（图中点状线是观测值，实线是计算值）

5 与台风增水的数理统计方法的比较

闸坡验潮站与沙环验潮站距离较近，所以我们将根据沙环验潮站1990年3月至1991年3月的潮位资料，分离出沙环验潮站的增减水值，参照台风资料，建立了沙环验潮站和闸坡验潮站增水的线性相关，相关系数为0.83。

相关公式为：

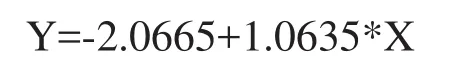
式中，Y为沙环验潮站的增水，X为闸坡验潮站的增水，单位为cm。

我们对闸坡验潮站1962—1996年的潮位资料进行了分离，建立了闸坡验潮站的台风增水年极值系列（表略）。根据沙环验潮站和闸坡验潮站增水的线性相关关系，建立了沙环验潮增水极值系列（表略），沙环验潮站的重现期（龚贝尔（Gumbel）方法）增水（见表6）。

采用皮尔逊III型计算沙环站台风增水（订正）重现期见表7，Cv=0.400，（Cs/Cv）＝4。

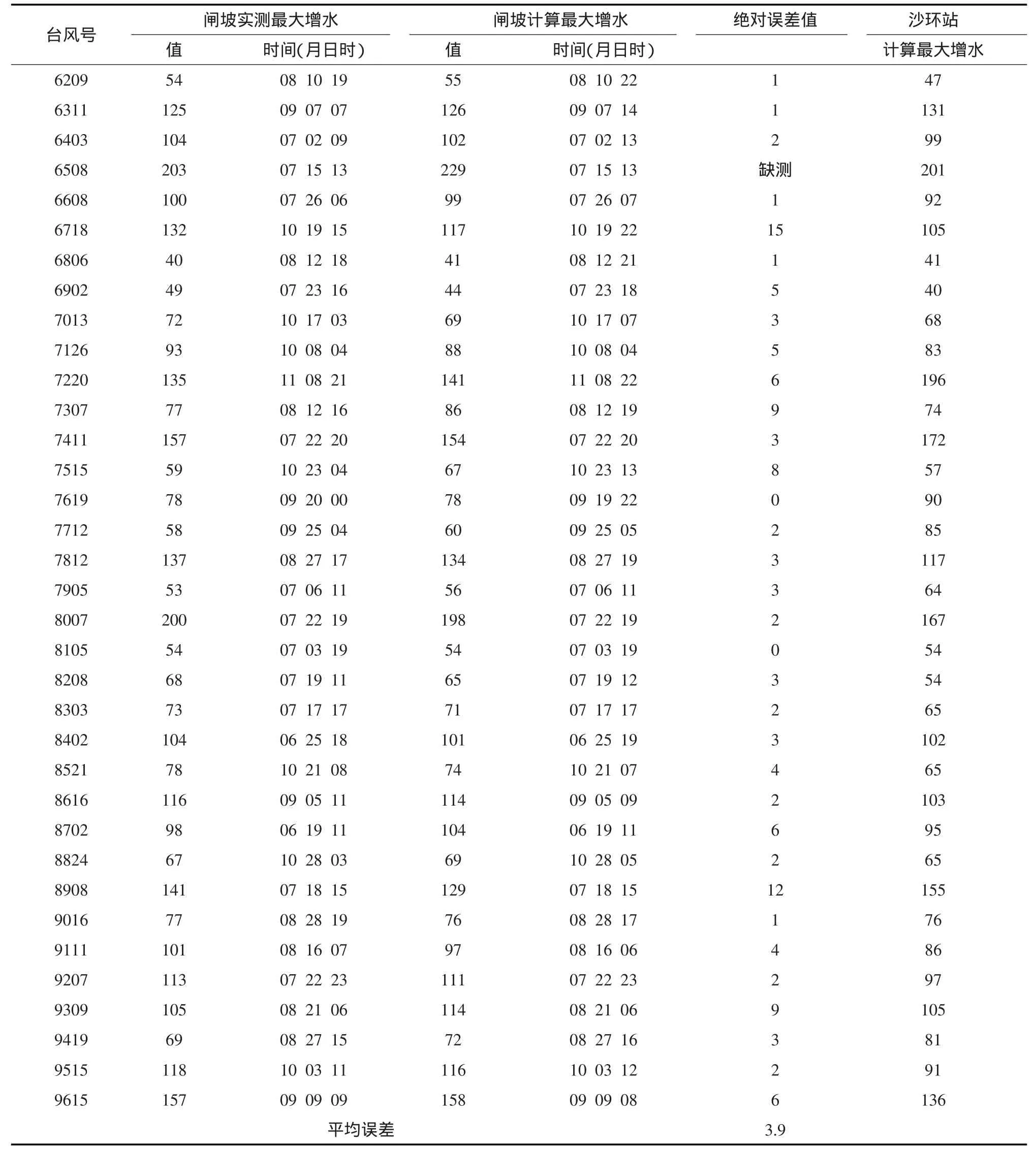
表3 数值方法计算闸坡站和核厂址处（沙环）年极值台风增水样本（单位：cm）

表4为利用风暴潮数值模式计算的沙环站重现期风暴潮龚贝尔（Gumbel）方法计算结果，表5为利用风暴潮数值模式计算的沙环站重现期风暴潮皮尔逊III型计算结果。而表6则为利用闸坡站与沙环站的相关关系计算的沙环站重现期风暴潮龚贝尔（Gumbel）方法计算结果，表7为利用闸坡站与沙环站的相关关系计算的沙环站重现期风暴潮皮尔逊III型计算结果。从表1—4可以看出：利用风暴潮数值模式计算的沙环站重现期风暴潮，无论是采用龚贝尔（Gumbel）方法，还是采用皮尔逊III型计算方法，其计算精度都与利用闸坡站与沙环站的相关关系计算的沙环站的重现期风暴潮相应的统计方法相当。如果把利用闸坡站与沙环站的相关关系计算的沙环站的重现期风暴潮值作为准确值，那么利用风暴潮数值模式计算的沙环站的重现期风暴潮的相对误差与绝对误差列于表8和表9中。

表4 沙环站数值模拟极值系列龚贝尔(Gumbel)方法重现期计算结果

表5 沙环台风增水重现期皮III型计算结果

表6 沙环台风增水（订正）重现期龚贝尔（Gumbel）方法计算结果

表7 沙环台风增水（订正）重现期皮尔逊III型计算结果

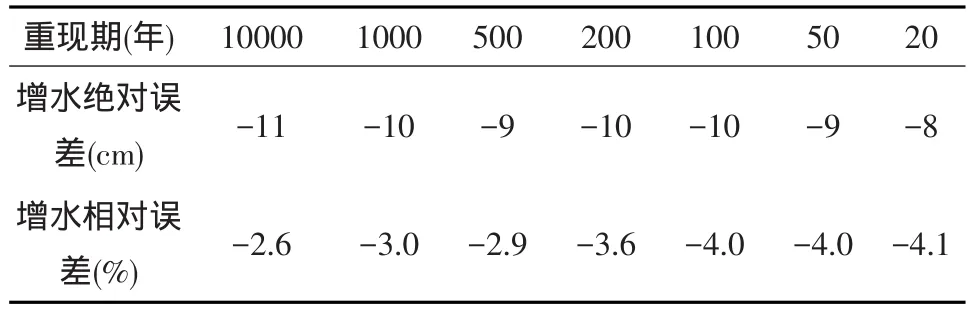
表8 沙环站数值模拟极值系列龚贝尔（Gumbel）方法重现期计算误差

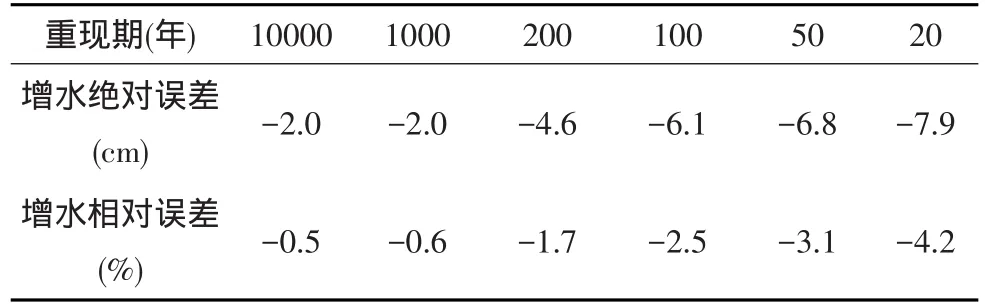
表9 沙环站数值模拟极值系列皮III型方法重现期计算误差

从表8、表9中可以看出，对于利用风暴潮数值模式计算的沙环站的重现期风暴潮这种新方法，如果采用龚贝尔（Gumbel）方法计算重现期，其绝对误差在各个重现期差别不大，均为-10 cm左右，即计算结果均比通常的方法偏小，这可能使模式的系统误差所致。其相对误差随着重现期的增大而减小，范围为-2.6%—4.1%之间。如果采用皮尔逊III型方法计算重现期，其绝对误差比采用龚贝尔（Gumbel)方法小，并随着重现期的增大而减小，但是计算结果也都比通常的方法偏小。同样，其相对误差随着重现期的增大而减小，范围为－0.5%至-4.2%之间。无论如何，利用风暴潮数值模式计算的沙环站的重现期风暴潮这种新方法，在计算精度上是令人满意的，对于海洋工程点的初步论证是可信的。特别对于没有任何观测资料的工程点，这种方法是一种非常好的方法。

6 结论

本文提出一种利用风暴潮数值模式计算工程点的重现期风暴潮的计算方案，即利用验证的风暴潮数值模式计算出工程点每年最大的风暴潮序列，然后利用该序列进行重现期风暴潮的统计计算。以计算广东阳江市沙环站为例，计算了沙环站的重现期风暴潮，并与通常的方法进行了比较，计算结果表明，此方法与通常采用的方法相比，精度相当，这对于那些无长时间序列验潮资料的工程点，特别对于那些没有一点观测资料的工程点，计算重现期风暴潮，提供了一种较为可靠的计算方案。但是，采用这种方法需注意以下几个问题：（1）风暴潮数值模式必须是经过大量观测资料验证的非常可靠的模式；（2）验证模式的观测站必须离工程点比较近，以保证工程点风暴潮计算的可靠性。

[1]Jelesnianshi C P,Chen J,Shaffer W A.SLOSH:Sea,Lake,and Overland Surge from Hurricanes[R].NOAA Technical Report NWS48,1992:71.

[2]秦曾灏,冯士笮.浅海风暴潮动力机制的初步研究[J].中国科学,1975,18(1):64-78.

[3]Sun W X,Feng S Z,Qin Z H.Numerical Study on the Bohai Sea Wind Surges-The Zeroth-Order Dynamical Model[J].ACTA Oceanologica Sinica,1982,1(2):175-189.

[4]Wang X N,Yu F J,Yin Q J.Research of Application of Numerical Models of Typhoon Surges in China Seas[J].Mausam,1997,48(4):595-608.

[5]冯浩鉴,于福江,方爱平.GIS支持下的风暴潮漫滩计算与减灾防灾-中国东部沿海地区海平面与陆地垂直运动[M].海洋出版社,1999:26-35.

[6]葛黎丽,屈衍,张志旭,等.南海深水区风、浪、流多年一遇重现期极值的推算[J].中国海上油气,2009,21(3):207-210.

[7]于宜法,俞聿修.渤海天文-风暴潮数值模拟和一种多年一遇极值水位的计算方法[J].海洋学报(中文版),2003,25(4):10-17.

[8]赵滨,张平,汪景庸.渤海埕北海域风暴潮多年一遇极值增水的数值计算[J].黄渤海海洋,2000,18(3):14-19.