基于BP神经网络的臭氧需求量预测方法的设计

郭华芳，张羽翔，尹 华

（1.中国科学院广州能源研究所，广东 广州510640；2.中国科学院可再生能源与天然气水合物重点实验室，广东 广州510640；3.广东工业大学，广东 广州510006）

1 技术背景

煤炭燃烧产生的烟气中，含有大量的氮硫氧化物，这些氧化物直接排放到空气中，会导致酸雨等自然灾害的发生。因此，各国都在积极研究烟气脱硫脱硝技术。目前最新的技术是采用臭氧的强氧化性对烟气中的NO进行处理，使之溶解于水，降低烟气中的氮硫氧化物。

现有的技术对于臭氧的添加采用的是PID控制，此控制技术经过多年的发展，已经相对成熟。其控制设备简单，控制思路清晰，但在控制过程中也存在很多问题，比如对于大惯性环节控制滞后，震荡过度等问题。在添加臭氧的过程中，通过检测烟气输入端的氮硫氧化物的摩尔量，利用反应方程式计算理想状态下需要的臭氧摩尔量，然后再通过检测通入碱性废水中和前的NOx，SO2的浓度，完成PID调节，改变臭氧的添加量。

在添加的过程中，因为影响臭氧添加量的各个因素之间是非线性的，所以无法进行单一的线性补偿，导致臭氧添加量过大或者过少。过大会造成添加臭氧的浪费，过小会使烟气反应不完全，导致烟气排放不达标，所以本发明的目的就是根据历史数据对臭氧的需求量建立预测模型，通过数据的分析，预测臭氧的消耗量，以达到减少浪费或者减少烟气不达标的情况。

人工神经网络是利用计算机模拟人脑的结构和功能的一门新学科［1］，能够利用自身的优良处理性能，解决高度非线性和严重不确定性系统的复杂问题，在此适合进行对臭氧需求量进行预测，所以提出建立一个三层BP神经网络预测模型，使用改进的算法进行训练，并对烟气脱硫脱硝中臭氧需求量的预测的方法［2］。

2 BP网络及动量梯度下降算法

BP（Back Propagation）网络是1986年由Rumelhart和McCelland为首的科学家小组提出的，一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入－输出模式映射关系，并且无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层（input layer）、隐含层（hide layer）和输出层（output layer）。

BP网络学习规则又称为 学习规则，对于给定的一组训练模式，不断用一个个训练模式重复前向传播和误差反向传播过程，各个训练模式都满足要求时，则说明BP网络已学习好了。从网络学习的角度来看，网络状态前向更新及误差信号传播过程中，信息的传播是双向的，但是不意味着网络层与层之间的结构也是双向的。

BP神经网络能够以任意精度逼近任何非线性连续函，使得其特别适合于求解内部机制复杂的问题，即BP神经网络具有较强的非线性映射能力；其次BP神经网络具有高度自学习和自适应的能力。还有泛化能力，即BP神经网络具有将学习成果应用于新知识的能力。容错能力：BP神经网络具有一定的容错能力，即使系统在受到局部损伤时还是可以正常工作（图1）。

图1 误差方向传播学习算法示意图

Levenberg－Marquardt算法作简要阐述，设误差指标函数为

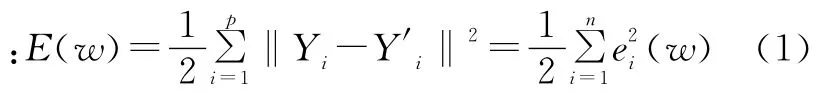
式中：Yi为期望的网络输出向量；Y′i为实际的网络输出向量；p为样本数目；w为网络权值和阈值所组成的向量；ei（w）为误差。

设wk表示第k次迭代的权值和阈值所组成的向量，新的权值和阈值所组成的向量为＝wk＋Δw。在LM方法中，权值增量Δw计算公式如下：

式中：I为单位矩阵；μ为用户定义的学习率；J（w）为Jacobian矩阵［3］，即：

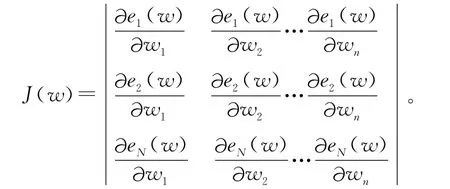
从（2）式可看出，如果比例系数μ＝0，则为高斯－牛顿法；如果μ取值很大，则LM算法接近梯度下降法，每迭代成功一步，则μ减小一些，这样在接近误差目标的时候，逐渐与高斯－牛顿法相似［4］。高斯－牛顿法在接近误差的最小值的时候，计算速度更快，精度也更高。由于LM算法利用了近似的二阶导数信息，它比梯度下降法快得多，实践证明，采用LM算法可以较原来的梯度下降法提高速度几十甚至上百倍。另外由于［JT（w）J（w）＋μw］是正定的，所以（2）式的解总是存在的，从这个意义上说，LM算法也优于高斯－牛顿法，因为对于高斯－牛顿法来说，JTJ是否满秩还是个潜在的问题。

在实际的操作中，μ是一个试探性的参数，对于给定的μ，如果求得的 能使误差指标函数 降低，则E（w）降低；反之，则μ增加。用（2）式修改一次权值和阈值时需要求n阶的代数方程（n为网络中权值数目）。LM算法的计算复杂度为O（n3/6），若n很大，则计算量和存储量都非常大。然而，每次迭代效率的显著提高，可大大改善其整体性能，特别是在精度要求高的时候［5］。

3 臭氧脱硫脱硝需求量的预测

以BP神经网络模型为原始模型，建立一个三层BP神经网络预测模型，使用改进的算法进行训练，并对烟气脱硫脱硝中臭氧需求量的预测［6］，主要步骤分析为以下几个方面。

（1）根据生产工艺流程，臭氧将难溶于水的NOx，SO2等氮硫氧化物氧化成易溶于水的高价氧化物，通过碱性废水进行中和，同时脱硫脱硝的目的。通过分析可知，影响臭氧需求量的主要因素是：烟气的流速，反应前烟气中氧气的浓度，反应中管道内的平均氧气浓度，反应管道中臭氧与SO2的摩尔比，臭氧与NOx的摩尔比，气体在反应管道中的停留时间，碱性废水吸收液的温度，碱性废水吸收液中碱离子的浓度和烟气的温度等因素。在此，选取以上影响因素作为BP神经网络模型的输入变量，通入的臭氧的流速作为输出变量。

在建立BP神经网络模型过程中，隐含层节点数对BP神经网络预测精度有较大的影响，节点数太少，网络不能很好地学习，需要增加训练次数，训练的精度也受影响；节点数太多，训练时间增加，网络容易过拟合［7，8］。最佳隐含层节点数的选择可参考如下公式。

式中，n为输入层节点数；l为隐含层节点数；m为输出层节点数；a为0～10之间的常数。在实际问题中，隐含层节点数的选择首先是参考公式来确定节点数的大概范围，然后用试凑法确定最佳的节点数。

（2）臭氧需求量预测中样本数据的采集与训练。根据步骤（一）得出的影响臭氧需求量的主要因素，在实验室条件下，进行相关数据的收集，以此作为BP神经网络模型的学习样本，对网络进行训练，确定臭氧需求量预测模型的网络参数；

在预测模型中，可以设系统的期望预测值为yk′（k＝1，2，3，…，n）对应的网络实际输出值为yt（t＝1，2，3，…，n），预测误差为e。其中误差e用公式描述入公式（5）：

取均方误差E作为此神经网络预测系统的性能评价指标之一，公式为：

输入训练样本数据，采用BP算法训练网络，直到收敛于一定的误差标准。否则，可以重新改变网络的初始权值或者网络的拓扑结构，直至训练结果满意为止［9］。

（3）将实际采集到烟气参数输入到臭氧预测模型中，预测此工况下的臭氧需求量。

（4）根据预测值控制臭氧的添加量，测量尾气中各含量参数，验证方法的准确性。

综上所述整体流程如图2所示。

结合以上步骤的分析，初步设计了试验步骤如下：首先混合多种气体，模拟烟气成分，并且测算各浓度比，如图3中模拟烟气系统。通过神经网络算法预测臭氧的需求量，并且通过控制器来控制臭氧的添加量，在氧化反应瓶中进行反应，如图3中烟气氧化系统。通过碱性水喷淋系统，对烟气中氮硫氧化物进行吸收，如图3中烟气吸收系统。最终尾气经过除湿系统，成分分析系统，最后排放，如图3中烟气分析系统。

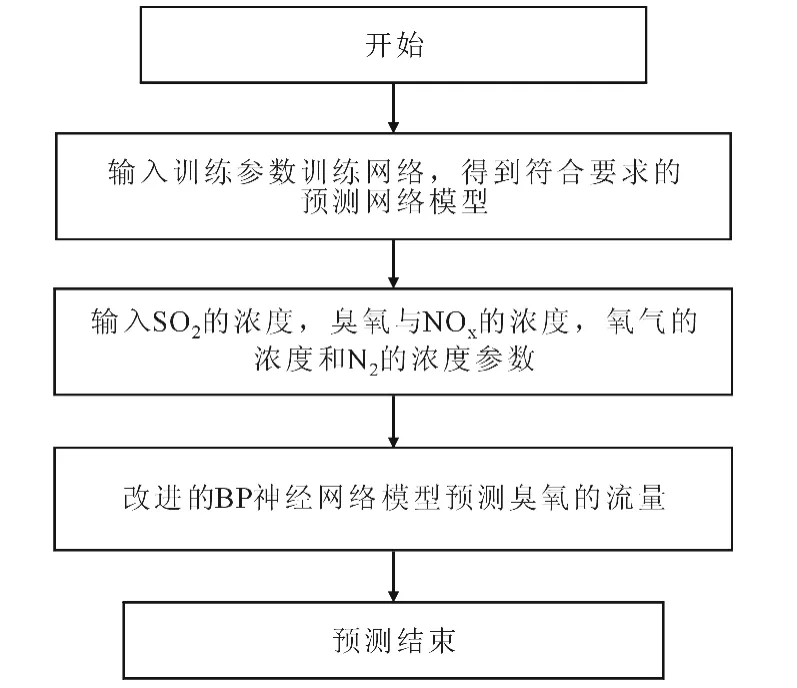
图2 利用神经网络预测臭氧添加量

图3 实验室技术方案设想

4 结语

改进的BP网络预测模型，对同时脱硫脱硝臭氧需求量进行预测，训练算法采用动态自适应学习率的梯度下降算法，能够更快的进行训练，预测误差也较小，预测值有很好的利用价值；通过对臭氧需求量的预测，能够实时的根据工况自动改变臭氧的添加量，既能满足脱硫脱硝的技术要求，同时也可以降低臭氧的需求量，降低企业成本，提高公司效益。本文只是设计了方法，结果需要经过试验进行验证，并进行改进。

［1］吴昌设.基于人工神经网络的电网日负荷预测研究［D］.杭州：浙江大学，2011.

［2］姜成科.基于遗传算法的神经网络在大坝变形预报中的应用［D］.大连：大连理工大学，2008.

［3］刘晓悦，姚乐乐，聚类分析在超短期电力负荷中的应用［J］.河北联合大学学报：自然科学版，2013，35（3）：74～80.

［4］沙瑞华.基于神经网络的水电机组动载识别研究［D］.大连：大连理工大学，2005.

［5］黄豪彩，杨冠鲁.基于LM算法的神经网络系统辨识［J］.组合机床与自动化加工技术，2003（2）：6～8.

［6］冯居易，郭 晔.基于LM算法的石油期货价格预测研究［J］.技术经济与管理研究，2009（5）：19～21.

［7］项 灏，张 俊.一种改进的量子遗传模拟退火算法及其在神经网络智能故障诊断中的应用［J］.机床与液压，2012.40（13）：196～200.

［8］李 欣，程春田，曾 筠.基于改进量子遗传算法的过程神经元网络训练［J］.控制与决策，2009，24（3）：347～351.

［9］黄金侠，金宁德.转炉冶炼终点静态控制预测模型［J］.炼钢，2006，22（1）：45～48.