装备保障多配送中心连续选址模型及其算法研究

王莉莉，陈云翔，刘 阔，王 政

（1.空军工程大学 装备管理与安全工程学院，陕西 西安 710051；2.国网南阳供电公司，河南 南阳 473000；3.94672部队，江苏 南京 211100）

0 引 言

装备配送中心是装备保障力量的重要组成部分，平时是军队战备训练物资的储备、供应基地，战时担负军队装备、弹药、器材的供应保障任务，加强装备保障配送中心建设，提高装备供应保障能力，对保持部队持续作战能力和作战胜利起着至关重要的作用。在整个装备供应网络中，配送中心[1]作为装备周转、分拣、库存管理和流通加工的据点，能克服装备在运输过程中产生的时间和空间障碍，保证装备满足不同作战单位的需求。好的装备保障配送方案，不仅能够节约物流成本，提高装备运输速度，而且还可以实现装备保障的系统化、集成化、库存结构合理化、装备储备数量科学化。

由于装备保障范围内的路网结构密集，且配送中心选址目标区域是一个连续的平面区域[2]，可能选址位置的数量是无限的，配送中心与配送中心之间的距离一般通过在地图上直接测量可以得到，处理方便。因此，这里推荐使用连续选址方法[3]进行装备保障配送中心的选址。一般情况下，装备保障配送中心选址通常是以总配送费用最少为目标函数建立选址模型，而战争中呈现出的高消耗性和高时效性等特点，使得装备保障配送中心的选址不仅要满足总配送费用最小外，还必须满足配送时效性的要求。同时，为了减小装备保障配送中心在战时受攻击的概率，实现配送中心安全、可靠的要求，装备保障配送中心选址必须根据敌方火力的攻击能力确定出安全性约束条件。

1 装备保障多配送中心选址的基本程序（如图1所示）

图1 装备保障多配送中心选址的基本程序[4]

2 装备保障多配送中心连续选址模型

2.1 基本假设

给定某战区，在此区域内分布着执行不同任务的作战单元，要求在此区域内拟建一定数目的装备保障配送中心，为多个需求地提供作战物资配送服务，选址的总原则[5]是尽量使选出地址上建立的配送中心与各需求地的总配送费用最小，总配送时间最少。基本假设如下：（1）运费是运输量、运输距离的函数；（2）一个需求地仅有一个配送中心供应；（3）配送中心容量可以满足需求；（4）各需求点的需求量已知；（5）需求地在整个装备物流系统中权重不同，在配送过程中考虑先配送权重大的需求地；（6）用地理坐标求出的装备保障配送中心和装备器材、弹药需求地的距离作为模型中配送中心和需求地之间的计算距离，不考虑之间实际里程。

2.2 根据费用最小确定多配送中心位置

（1）基本假设

Cyij表示装备保障配送中心i向需求地j供应过程中的总运输费用；（xj, yj）表示需求地j的位置坐标；（Xi,Yi）表示装备保障配送中心i的位置坐标；dij表示装备保障配送中心i到需求地j的距离；Dj表示需求地j的最大允许配送距离；m表示需求地数；n表示装备保障配送中心数；q表示运输方式数；bijq表示不同运输方式下装备保障配送中心i和需求地j之间单位距离、单位物资运输费（bij1：航空运费，bij2：铁路运费，bij3：公路运费，bij4：水运费）；wijq表示以运输方式q将装备从配送中心i运到需求地j的运输量；aij表示从配送中心i到需求地j的单位距离运输费；pj表示需求地j的需求量；Zij为0、1变量，表示需求地j是否由设置于点i的配送中心供应；y=e（x）表示约定的火力打击范围；（xa1, ya1）表示装备保障配送区域的起始点坐标；（xa2, ya2）表示装备保障配送区域的终止点坐标。

（2）选址模型

模型的目标函数为：

2.3 根据时间最短确定多配送中心位置

（1）基本假设

Tyij表示从配送中心i向需求地j的运输时间之和；（Xi,Yi）表示装备调配保障配送中心i的位置坐标；dij表示装备调配保障配送中心i到需求地j的距离；Dj表示需求地j的最大允许配送距离；m表示需求地数；n表示装备调配保障配送中心数；q表示运输方式数（航空，铁路，公路，水运）；vijq表示配送中心i到需求地j每一段路程中，不同运输方式的运输速度；γijq表示从配送中心i到需求地j的运输过程中，每一段路程的相对难易程度；fijq表示每种运输方式在从配送中心i到需求地j的路程中所占的比例；λj表示需求地的权重；Zij为0、1变量，表示需求地j是否由设置于点i的配送中心供应；y=e（x）表示约定的火力打击范围；（xa1, ya1）表示装备调配保障配送区域的起始点坐标；（xa2, ya2）表示装备调配保障配送区域的终止点坐标。

（2）选址模型

模型的目标函数为：

3 装备保障多配送中心连续选址模型的求解

配送中心的连续选址问题可以看作一个多源Weber问题。该问题假设配送中心没有容量限制，任何一个需求地的需求量都由离它最近的配送中心满足。Cooper[6]已证明该问题的目标函数既不是凸函数也不是凹函数，有可能存在许多局部最优解，因此对于大规模的连续选址问题，多采用启发式算法。多配送中心连续选址不但要同时确定多个配送中心地址，还要确定每个配送中心服务分配方案，所以又称为连续选址分配问题[7-8]。目前对连续性选址模型的求解方法[9-10]一般以重心法为基础进行计算，但是在选址中由于存在较多局部解，用常规算法很难得到最优解，因此能够找到一种进行全局优化的方法显得尤为重要[11]。基于这种考虑，以费用最小的配送中心选址模型为例，本文分两步求解[12]选址模型，第一步，暂时不考虑时效性约束（4）和安全性约束（6），仅从节省费用的角度出发，用目标函数（1）和约束条件（2）、（3）、（5）进行选址计算，确定每个配送中心所服务的需求地集合，用服务分配矩阵来描述。第二步，考虑时效性约束条件（4）和安全性约束条件（6），用MATLAB优化函数分别对每个配送中心进行选址计算，确定最终符合经济性、时效性和安全性约束的选址方案。

3.1 交替分配启发式算法

根据提供的n个配送中心地址（X1,Y1）,（X2,Y2）, …,（Xn,Yn）确定离每个需求地最近的配送中心为该需求地供应装备，形成n个配送区域，每个区域可表述为如下的需求地集合：

要求总费用最小，则对Xi、Yi求偏导，令其为0。

由式（13）可以求得区域Qi内最优配送中心地址的坐标（X*i,Y*i）。

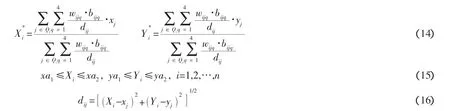
利用式（14），假设一个初始解（x0i,y0i），把（Xki,Yki）代入式（14）、（15）和（16）中，计算出装备保障配送中心的改善地址（Xki+1,Yki+1）。当相继得出的解（Xki,Yki）和（Xki+1,Yki+1）充分接近时，既可停止计算，（Xki+1,Yki+1）便是i个配送中心作为单一新增配送中心的最优解。

一个有确定值的二进制数矩阵（lij）m×n就代表一种备选的服务分配方案，但是由于备选方案总共有S（n,m）种当m、n数变得较大时，备选方案的数目可能非常大，因此，构造出交替分配启发式算法，确定装备保障配送中心连续选址的服务分配矩阵，具体步骤如下：

（1）将n个服务对象任意分成m个组，每个组有一个配送中心负责送货，从而初步确定服务分配矩阵S，S=（lij）m×n。

（2）按式（14）、（15）和（16）进行迭代计算，直到充分接近为止，求出配送中心的坐标，计算总配送费用。

（4）重复第2和3两步运算过程，直到所有服务对象都划归到为总配送费用最少的装备保障配送中心负责供货为止。此时，方案最佳，各配送中心地址为最优地址，总配送费用最小。

3.2 考虑时效性和安全性约束的模型求解

本文同时考虑经济性、时效性和安全性的选址模型是一个有约束非线性规划的问题，可以借助MATLAB优化工具箱中的fmincon（）函数进行选址计算。

目标函数：

时效性约束：

安全性约束：

选址坐标的上下限：

fmincon（）函数调用格式[13]为：［x,fval］=fmincon（@fun,x0,A,b,Aeq,beq,bl,ul,@con,@eon）

x是输出的选址结果，fval是输出目标函数值，即最小配送费用。fun是用MATLAB语言编写的目标函数M文件，con是用MATLAB语言编写的时效性约束M文件，eon是用MATLAB语言编写的安全性约束M文件。bu、ul分别是配送中心坐标取值的上限下限，A、b、Aeq、beq为空集。x0为初始可行解。初始可行解是寻优搜索的起点位置，本文把它定位在配送区域中心位置，令：

最后，把上述M文件和输入参数一起代入fmincon（）函数中，很快输出选址结果［X,Y ］，如果无解，则应该增加配送中心数量，以满足装备保障配送的时效性和安全性要求。

4 结论

本文结合我军装备保障的现状以及未来担负的主要作战任务和可能的作战环境，对装备保障多配送中心的连续选址问题进行了分析与讨论，以经济性为目标函数，以时效性和安全性为约束条件，给出了装备保障多个配送中心连续选址模型。由于多配送中心连续选址不但要同时确定多个配送中心地址，还要确定每个配送中心服务分配方案，所以，本文利用交替分配启发式算法对模型进行求解，把多个配送中心连续选址问题转化为单个配送中心连续选址问题，最后再运用MATLAB优化工具箱中的fmincon（）函数对每个配送中心的地址进行计算，得到最优配送中心地址。本文提出的算法已为我军某作战方向的装备器材弹药配送网络规划所借鉴，能够有效解决装备保障选址中的时效性和安全性约束问题，结果符合实际要求。

[1] 汝宜红，田源，徐杰.配送中心规划[M].北京：北方交通大学出版社，2002:10-46.

[2] Chen P C,Hansen P,Jaumard B,et al.Solution of the multisource Weber and conditional Weber problems by d.-c.programming[J].Operation Research,1998,46(4):548-566.

[3] Goldengorin B,Ghosh D,Sierksma G.Branch and peg algorithms for the simple plant location problem[J].Computer&Operations Research,2003,30(7):967-981.

[4] 甘应爱.运筹学[M].（修订版）.北京：清华大学出版社，2000:2-38.

[5] 刘志勇.空军装备保障配送中心选址研究[D].西安：空军工程大学，2003:18-20.

[6] Cooper L.Location-allocation problem[J].Operation Research,1963,11(1):331-343.

[7] 宋柏.物流系统多个仓库的定点决策方法[J].集装箱化，2000(10):9-12.

[8] 郭晓峰，郑隶华，叶耀华.基于最优配送线路的选址方法研究[J].物流技术，2001,109(4):28-30.

[9] Drezner T.Location of multiple retail facilities whit limited budget constraints-in continuous space[J].Journal of Retailing and Consumer Services,2000(3):173-184.

[10] 龚延成，郭晓汾，蔡团结,等.物流配送点选址模型及其算法研究[J].中国公路学报，2003,16(2):123-126.

[11] 姜大立，杨西龙.易腐物品配送中心连续选址模型及其遗传算法[J].系统工程理论与实践，2003(2):62-67.

[12] 龚延成.带时效性约束的配送中心多源选址问题研究[J].数学的实践与认识，2007,37(11):27-31.

[13] 苏金明，阮沈勇.MATLAB6.1实用指南[M].北京：电子工业出版社，2002.