基于信息共享的供应链双源渠道Stackelberg博弈分析

叶红雨，张家强，史元亭

（1.上海理工大学 管理学院，上海 200093；2.清华大学 经济管理学院，北京 100084）

0 引言

供应链下游细微的市场需求振动可能会对上游供应商造成计划的不确定性，其在供应链内部是理性人达到各自效用最大化的博弈结果[1]，即Lee等人所谓的牛鞭效应[2]。随着社会科技的发展，电子商务呈现蓬勃发展的趋势，供应链渠道由传统的单一渠道过渡到双源渠道并存，也改变供应链管理格局。消费者需求变化的不确定性、市场变化及产业变化等信息都会引起销售商之间或者销售商与供应商之间的博弈，这些都可能导致牛鞭效应的发生。为了削弱市场需求的振动，需要对供应链中各节点企业进行协调。

通常情况下，市场的需求不确定性影响企业的销售，继而影响到企业供应链的协调，供应链中各节点企业如何获取各种不确定信息并运用此来协调供应链，以达到对供应链系统最少的冲击的问题越来越受到理论界和企业界的重视。

针对供应链双源渠道问题的分析一直是研究供应链管理的学者们感兴趣的领域。一般，学者们通常只关注供应商如何使不同的商品分销给不同的零售商，以达到整体供应链收益最佳为目的的问题[3]。另外一些学者研究普通电子市场环境中供应链在双源渠道下如何达到供应商、零售商各自利益的协调[4]。随着信息共享对供应链管理的影响逐步加深，研究学者们开始关注信息共享对供应链双源渠道的影响效果和内部机制，认为信息共享在服务供应链背景下，对合作伙伴的绩效无明显的直接影响，但通过中间变量可以间接地影响到合作伙伴的绩效[5]。以及信息共享有助于减少供应链成本的问题[6]。邱若臻等认为信息共享下的供应及其各节点企业利润要高于无信息分享时的情况[7]。另外，李书娟等研究表明，在一定的条件范围内，零售商可以从信息分享中获利，零售商具有主动分享其私人信息的动机[8]；以及供应商和零售商在双渠道供应链中对信息共享的选择问题及企业会在什么情况下选择信息共享[9－10]。而张菊亮等研究供应链双方拥有部分信息的信息共享问题时，模型结果得出了双方都不愿共享私有信息的结论[11]。

对于信息共享为什么会影响到供应链协调呢？一种解释是零售商获得的市场需求不确定信息为了自己利益可以选择性地向供应商分享，以达到供应链的协调[12]。另一种解释是信息共享可以减少供应链中因需求不确定而导致的商品缺货或商品滞销等经济损失，可以更好制定生产计划和库存分配[13－14]。

在现有研究关于供应链基于双源渠道下的竞争分析中，仅仅考察信息共享只承担其在供应链系统博弈中的间接变量作用，却很少进一步分析市场需求不确定性在制造商和零售商中的利益博弈，而市场需求不确定性等的信息共享是制造商和零售商追求利益最大化过程中的选择性结果。零售商和制造商在面对市场需求不确定性需求时，总是选择对自己最有利的方式影响着供应链均衡。

综上，我们的研究对已有研究构成以下发展：在具有电子市场背景下的供应链双源渠道协调的主从对策模型[4]的基础上，创新性地加入了面对不确定的市场需求，零售商和制造商如何处理这种市场需求的不确定性，以使供应链各节点之间以及普通分销渠道与电子商务渠道之间的利润最优。

1 模型建立

当前电子商务特别引人注目，B2C、B2B等电子市场直销已经占了销售行业的半壁江山。由此，许多制造商在传统销售渠道的基础上开始谋求开发电子商务销售新渠道：传统渠道方面，制造商可以在已有的与零售商长期合作的基础上更加紧密的合作；电子商务渠道方面，制造商利用与零售商合作时共享的某些信息（市场调研、销售精细化分析等），可以选择是否充分利用到电子商务方面。电子商务背景下，供应链中信息共享的双源渠道架构如图1所示：

图1 电子商务背景下的供应链中信息共享双源渠道

1.1 符号说明

ae、at：传统市场基准需求量、电子商务市场基准需求量；

pe、pt：传统市场商品单价、电子商务市场商品单价；

b：价格需求弹性（b＞0）；

c：商品的单位成本；

θ：两种市场渠道间的需求扩散程度；

πr、πs：零售商利润、制造商利润；

t：市场需求不确定因素；

α：零售商获取需求不确定因素的成本；

β：零售商获取需求不确定因素的成本分担率；

x：制造商把需求不确定因素使用在电子商务渠道的程度。

1.2 基本假设

（1）制造商供应能力足够大，不会缺货，制造商和零售商都是风险中性的；

（2）消费者对于相同商品的购买意愿完全在于不同渠道的销售价格；

（3）制造商不能即时获取一线消费者的随机消费需求（不确定需求）和意愿，只能通过零售商的分享间接获取；

（4）零售商对于商品所提供的服务等在传统销售渠道的特殊资源，最终都体现在商品的零售价格中。

1.3 基本模型

设需求不确定因素t为随机变量，且服从于期望为0、方差为σ2的正态分布，即t～N（0,σ2）；t反应市场需求不确定性大小的信号，需求大时其值也大，需求小时其值也小。经济学中，商品需求量（d）与零售价格（p）之间在无需求不确定因素时：d=a-bp。当实际情况考虑到市场的需求不确定因素时，商品需求量（d）与零售价格（p）之间的关系如下：

其中：a,b为正常数。

晏妮娜等利用由传统分销渠道和电子直销渠道组成的双源渠道中考虑价格—服务的敏感性，构建了电子市场环境供应链双源渠道模型[4]。本文在此基础上，对价格—服务一体化处理（即传统渠道中顾客购买商品只考虑零售价格），加入市场需求不确定性因素，考虑只有一个制造商和一个零售商的供应链系统，分别构建零售商和制造商是否掌握市场不确定需求信息、零售商是否与制造商分享此信息，以及制造商如何利用市场不确定需求信息等几个模型。建立的模型如下：

模型一：零售商和制造商都不掌握市场的不确定需求信息t。

零售商利润：

制造商利润：

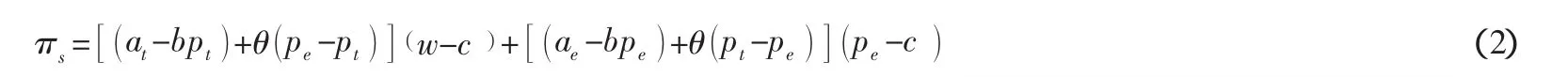
供应链整体利润：

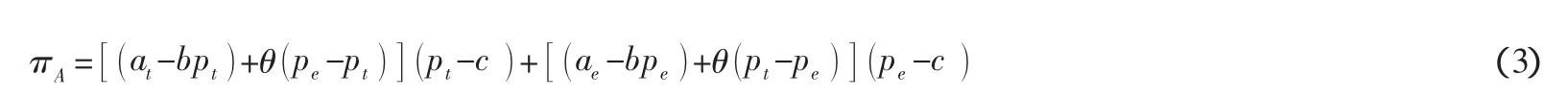
模型二：零售商掌握不确定需求信息t，但不与供应商分享。

零售商利润：

制造商利润：

模型三：零售商掌握不确定需求信息t，并与制造商分享，但制造商不把这些信息运用于电子商务市场。获取不确定需求信息的成本为α，与制造商分享此信息的成本分担率为β（0≤β≤1，β=1时为制造无尝获取此信息）。

零售商利润：

制造商利润：

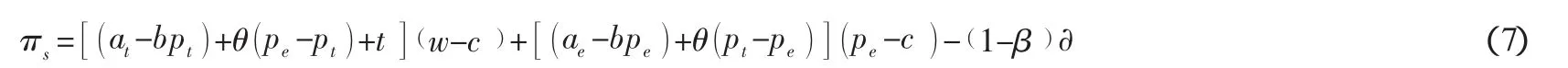
模型四：零售商掌握不确定需求信息t，并与制造商分享，而且制造商把这些信息运用于电子商务市场。设x 0＜x≤（）1为制造商把这些信息运用于电子商务市场的程度。

零售商利润：

制造商利润：

2 模型求解

在供应链系统中，制造商和零售商作分散决策时，Stackelberg主从博弈中，把制造商考虑为主方（Leader），零售商考虑为从方（Follower）。制造商的决策变量是批发价w和pe，零售商的决策变量是pt。使用逆向归纳法分析[15]，即有：

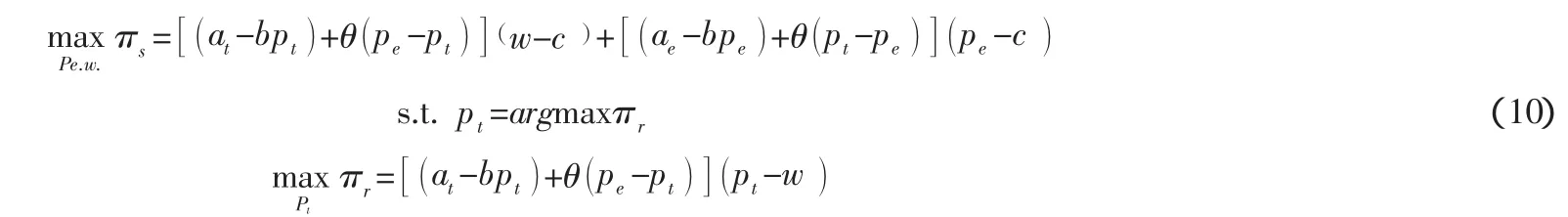
求解该主从决策在t～N（0,σ2）的前提下，得出各模型中的主从双方的Stackelberg均衡解：

模型一：

零售商最优利润：

制造商最优利润：

模型二：

零售商最优利润：

制造商最优利润：

模型三：

零售商最优利润：

制造商最优利润：

模型四：

零售商最优利润：

制造商最优利润：

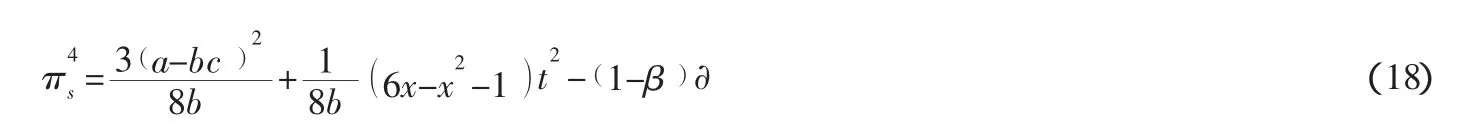
3 模型分析

3.1 零售商决策

从π1r和 π2r对比可看出，零售商通过是否掌握市场的不确定需求信息，在与制造商的博弈中，不能明显得出在掌握市场不确定需求信息的前提下，就可以获取更高的利润。在此需要考虑为了获取市场不确定信息的成本问题，但现在计算机的广泛使用，可以减少这项成本，甚至此项成本在可以忽略的前提下，零售商掌握市场不确定需求信息可以得到更高的利润。因此，零售商应当尽可能去获取市场的不确定需求信息。

从π2r和 π3r，π4r对比，忽略成本α时，可以看到π2r=π3r，π2r＞π4r。因为可以看到零售商在分享市场需求的不确定信息给制造商时，并不会提高自己的收益。因此，零售商掌握市场不确定需求信息时，可能不愿与制造商分享此信息。

3.2 制造商决策

从π1s和 π2s的对比，明显有π1s＞π2s，得出零售商掌握市场不确定需求信息，但不与制造商分享时，会减少制造商的利润。因此，制造商应该充分地与零售商保持沟通，并及时获取市场的不确定需求信息，以此来提高自己的收益。

从π3s和 π4s的对比，有π3s＜π4s，且随着 x（0＜1≤1）的增大，π4s－π3s的差值越来越大，由此可以得出制造商在掌握市场不确定需求信息时，把得到的此信息用于电子商务渠道会增加其利润，并且在电子商务渠道使用此信息程度的加深，利润也将逐步扩大。

3.3 整体决策

从π2r+π2s=π3r+π3s、π3r+π3s＜π4r+π4s、π2r+π2s＜π3r+π3s，可以看出：（1）零售商掌握需求不确定信息不管是否与制造商分享，此供应链的整体利益都不会增加；（2）当制造商获取了市场的不确定信息并用在了电子商务渠道上，此供应链的整体利益就必然增加。

4 结 论

本文分析了双渠道供应链在信息共享背景下的Stackelberg利润分配博弈，得出了各种情境下的均衡收益。当决策者把市场的不确定需求信息考虑到供应链各个环节中时，我们发现制造商在充分利用获取市场不确定需求信息时，不仅可以增加自己的利润，也可以增加供应链整体利润的结论。

本文为了分析的简便，把传统市场和电子商务市场的基准需求量统一，以及忽略了需求在两种渠道下的扩散。我们下一步的研究方向是增加需求在两种渠道的扩散程度，以及把传统渠道中的购物环境对消费者购买意愿和实际体验的影响考虑到模型当中。

[1] Forrester J.Industrial dynamics[M].New York:MIT Press and John Wiley&Sons,Inc,1961.

[2] LEE H L.Information distortion in a supply chain:The bullwhip effect[J].Management Science,1997,43(4):546－558.

[3] Scott C H,Scott J E.On models for the operation of a class of electronic marketplaces[J].Omega,2004,32(5):373－383.

[4] 晏妮娜，黄小原，刘兵.电子市场环境中供应链双源渠道主从对策模型[J].中国管理科学，2007,15(3):98－102.

[5] 姜荣，陈敬贤，杨琳.服务供应链信息共享、合作关系与企业绩效的关系研究[J].现代情报，2013,33(9):25－28.

[6] 孙静春，李双杰，方烨.非线性成本库存模型在易逝品供应链中的应用[J].系统管理学报，2013,22(1):10－16.

[7] 邱若臻，黄小原，葛汝刚.信息共享条件下供应链在线与传统销售渠道协调定价[J].管理工程学报，2009,23(4):74－78.

[8] 李书娟，张子刚.双渠道供应链预测信息分享的绩效研究[J].工业工程与管理，2010,15(5):40－43.

[9] Yue X,Liu J.Demand forecast sharing in a dual－channel supply chain[J].European Journal of Operational Research,2006,174(1):646－667.

[10] Yao D Q,Yue X,Wang X,et al.The impact of information sharing on a returns policy with the addition of a direct channel[J].International Journal of Production Economics,2005,97(2):196－209.

[11] 张菊亮，章祥荪.供应商和销售商拥有部分信息的信息共享[J].中国管理科学，2012,20(1):109－116.

[12] 张玉林，陈剑.供应链中基于Stackelberg博弈的信息共享协调问题研究[J].管理工程学报，2004,18(3):118－120.

[13] Chen F.Echelon reorder points,installation reorder points,and the value of centralized demand information[J].Management Science,1998,44:S221－S234.

[14] Gavirneni S,Kapuscinski R,Tayur S.Value of information in capacitated supply chains[J].Management Science,1999,45(1):16－24.

[15] 张维迎.博弈论与信息经济学[M].上海：上海人民出版社，1996:100－102.