关于h凸函数的加权三点不等式

时统业，吴 涵，宋祥斌

（海军指挥学院 浦口分院，江苏 南京 211800）

Simpson不等式在计算定积分的数值计算中有着重要的作用.近些年来，许多学者针对被积函数的各种情形，利用被积函数的各阶导数估计求积公式的误差.本文针对三阶可微函数，通过建立关于积分的恒等式，在三阶导函数的绝对值是h凸函数的情形下，利用简单的数学分析方法和Hölder不等式，给出若干带有权函数的三点不等式，并在特殊情况下得到有关文献的结果.

1 预备知识和引理

关于Simpson不等式的各种改进和推广，可参见文献［1－9］.文献［7－8］分别对其三阶导函数的绝对值是m凸函数和第二种意义上的s凸函数的可微函数建立了一些Simpson型不等式.

定义1［10］设h：J⊆R→R是取正值的函数，f：I⊆R→R是非负函数，且对于任意x，y∈I，t∈［0，1］，有f（tx＋（1－t）y）≤h（t）f（x）＋h（1－t）f（y），则称f是h凸函数.

关于h凸函数的性质和不等式可参见文献［9－16］.文献［9］考虑了三阶导函数的绝对值是h凸函数的可微函数，建立了一些Simpson型不等式，推广了文献［8］的结果.

定理A［9］设h：J⊆R→R（［0，1］⊆J）是非负函数，f：I⊆［0，∞）→R是int I上的三阶可微函数，a，b∈int I，a＜b，f（3）∈L1［a，b］.若｜f（3）｜是［a，b］上的h凸函数，则有

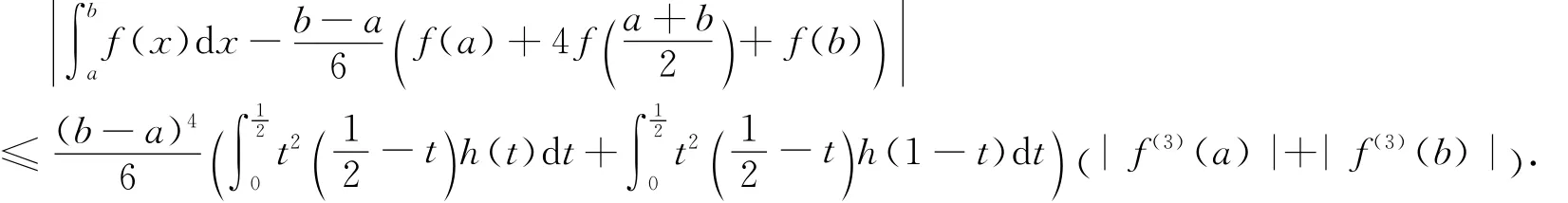
定理B［9］设h：J⊆R→R（［0，1］⊆J）是非负函数，f：I⊆［0，∞）→R是int I上的三阶可微函数，a，b∈int I，a＜b，f（3）∈L1［a，b］.若｜f（3）｜q是［a，b］上的h凸函数，且，则有

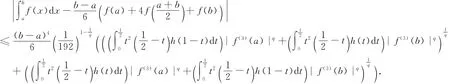
定理C［9］设条件同定理B，则有

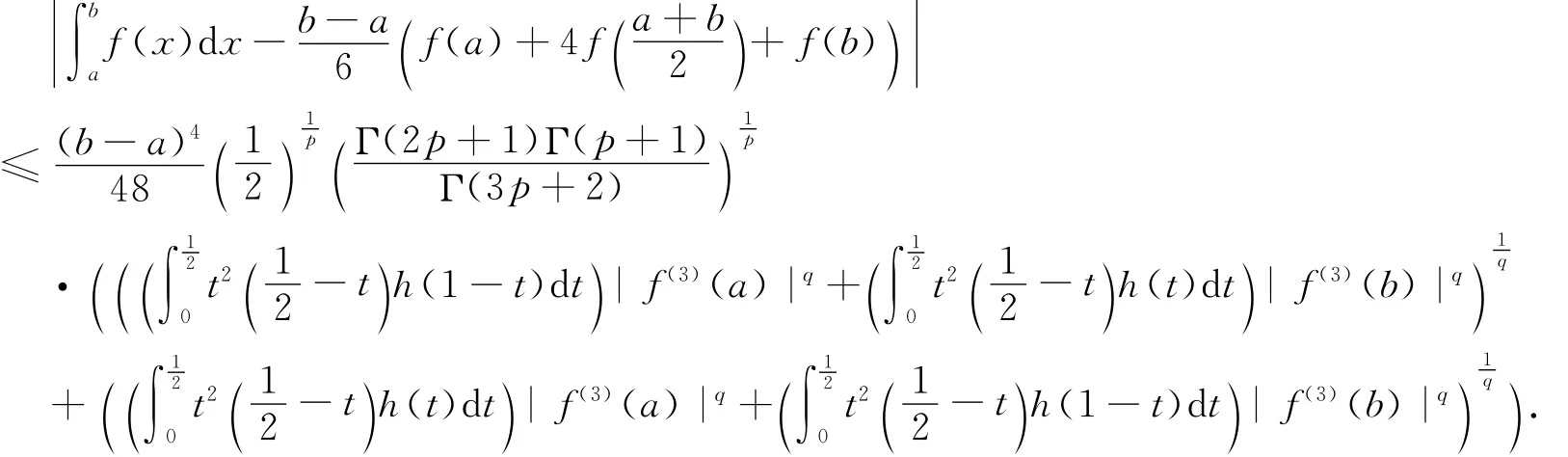
为了建立证明本文主要结论所用引理，引入函数k（x），并考虑其简单的性态.假设g：［a，b］→R是正的可积函数，定义

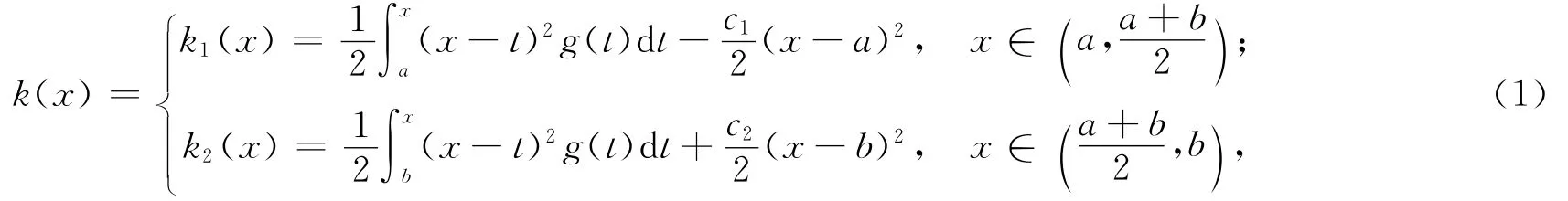
其中

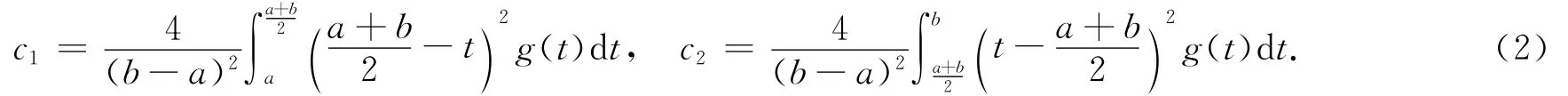
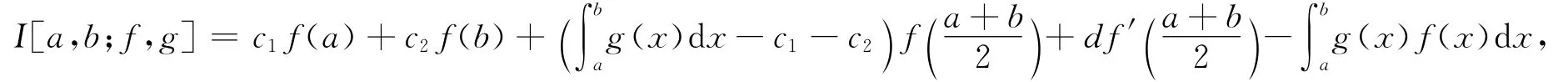
其中c1和c2如（2）式所定义，

引理1 设f：I⊆R→R是int I上的三阶可微函数，a，b∈int I，a＜b，f（3）∈L1［a，b］，g：［a，b］→R是正的可积函数，k（x）由（1）式所定义，则有

证 由分部积分法易证得，过程略.

引理2 设g：［a，b］→R是正的可积函数，k1（x）和k2（x）如（1）式所定义.若g≤M，M 为正常数，则有

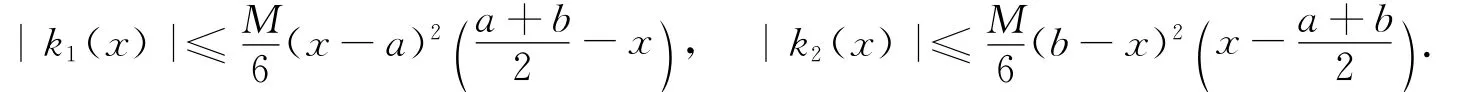
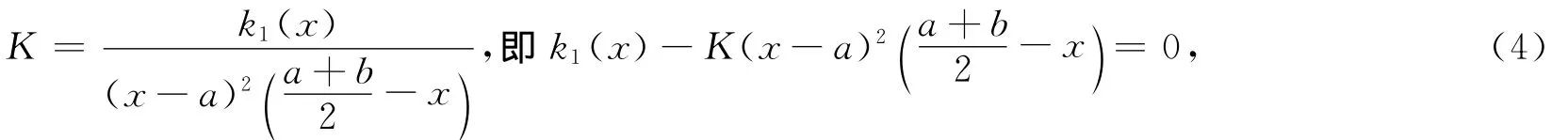
2 主要结果

定理1 设f：I⊆［0，∞）→R是int I上的三阶可微函数，a，b∈int I，a＜b，f（3）∈L1［a，b］，g：［a，b］→R是正的可积函数，h：J⊆R→R（［0，1］⊆J）是非负函数.若｜f（3）｜是［a，b］上的h凸函数，则有

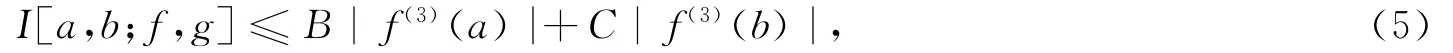
其中

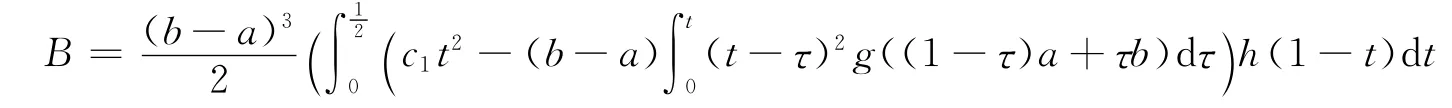
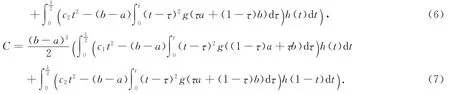
证 由引理1及｜f（3）｜的h凸性得

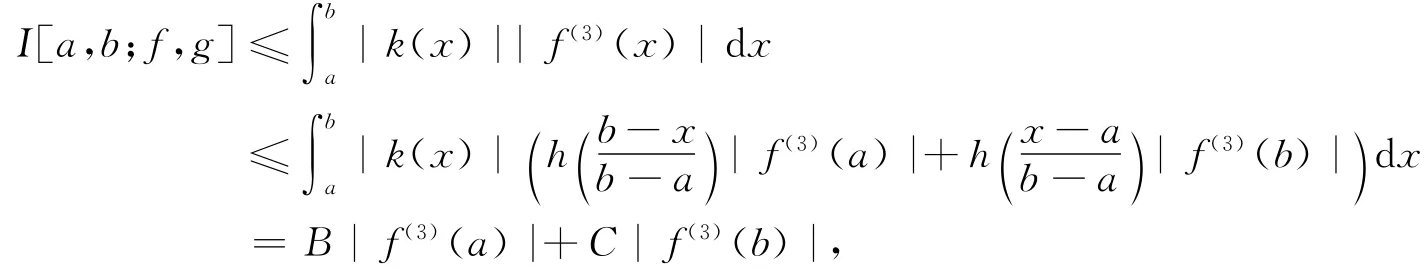
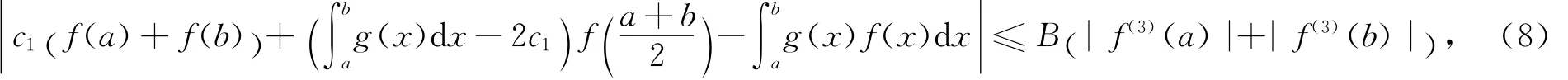
其中c1由（2）式所定义，

注1 在定理1中，若取g≡1，则可得定理A.

定理2 设f：I⊆［0，∞）→R是int I上的三阶可微函数，a，b∈int I，a＜b，f（3）∈L1［a，b］，g：［a，b］→R是正的可积函数，h：J⊆R→R（［0，1］⊆J）是非负函数.若｜f（3）｜q是［a，b］上的h凸函数，q＞1，则有

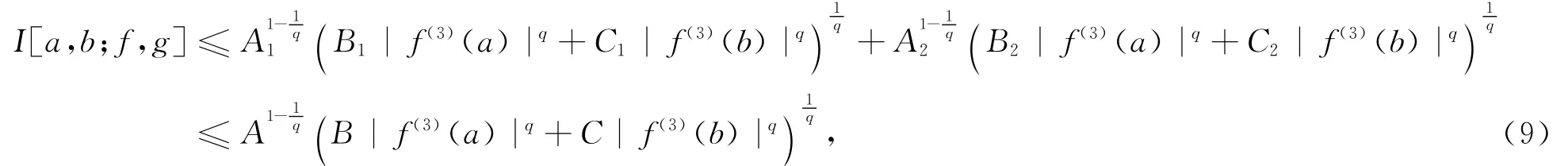
其中B，C的表达式分别由（6）式和（7）式所定义，

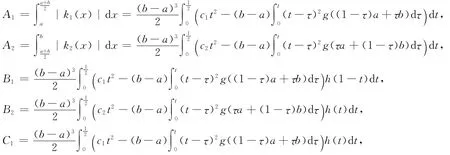
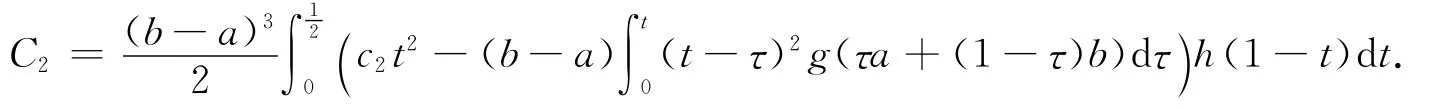
证 由引理1及Hölder不等式得

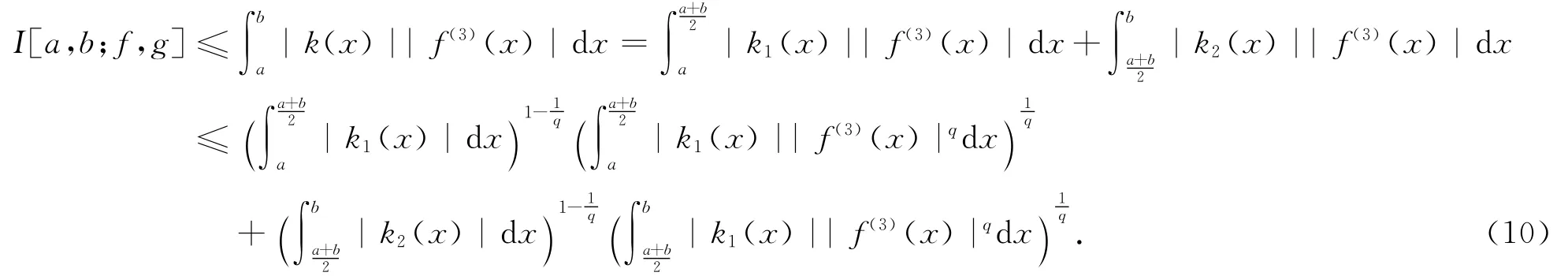
因为｜f″｜q是h凸函数，故有

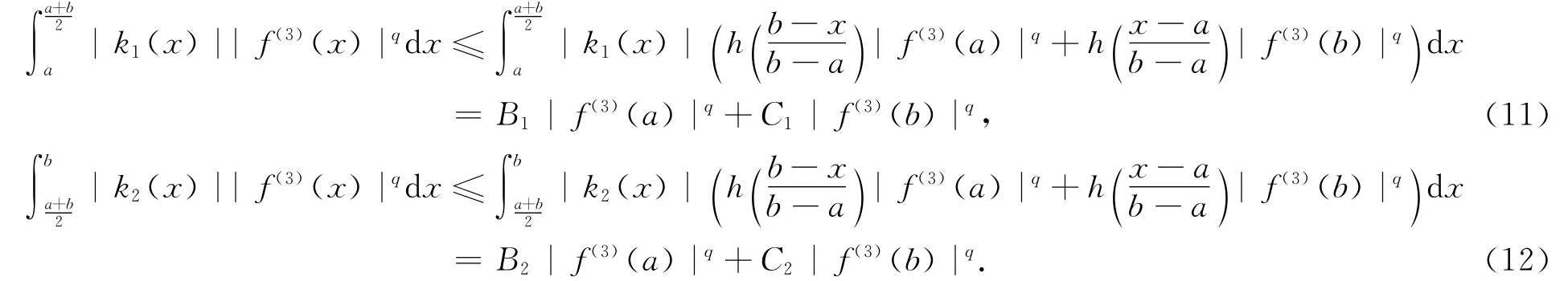
由（10）～（12）式得（9）式的左边不等式.利用 Hölder不等式，即对任意非负数a1，a2，b1，b2及任意的q＞1，有，可得到（9）式的右边不等式.定理2得证.

推论2 在定理2中，若又设g≤M，M是正常数，则有

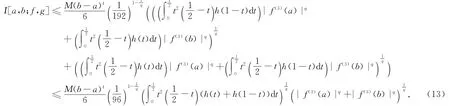
证 由定理2中A1，B1的表达式及引理2得

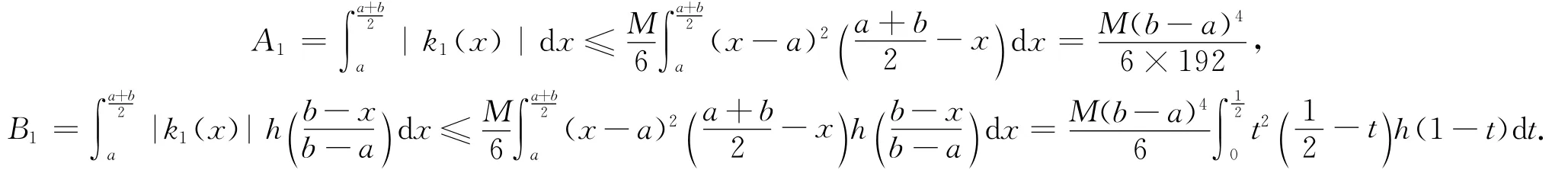
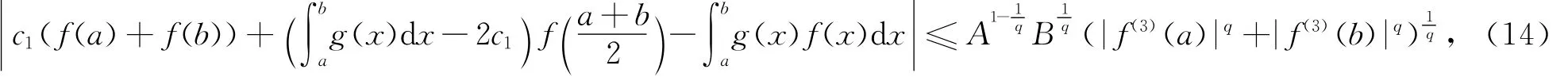
其中c1由 （2）式所定义，

注2 在定理2中，若取g≡1，则可得定理B.

定理3 设f：I⊆［0，∞）→R是int I上的三阶可微函数，a，b∈int I，a＜b，f（3）∈L1［a，b］，g：［a，b］→R是正的可积函数，g≤M，M 是正常数，h：J⊆R→R（［0，1］⊆J）是非负函数.若｜f（3）｜q是［a，b］上的h凸函数，，则有（其中Γ是Gamma函数.）

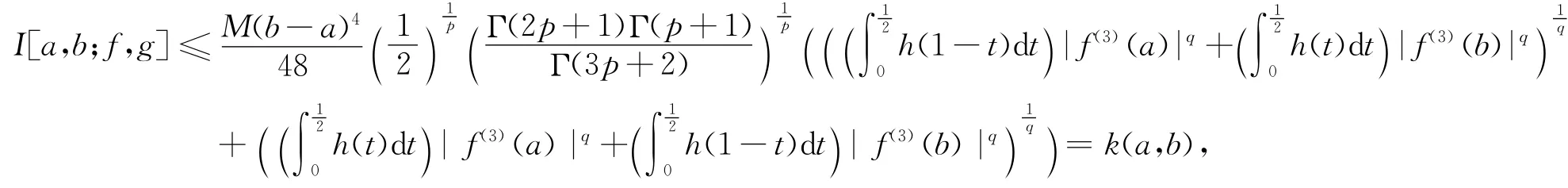
证 由引理1、引理2、Hölder不等式及｜f″｜q的h凸性得

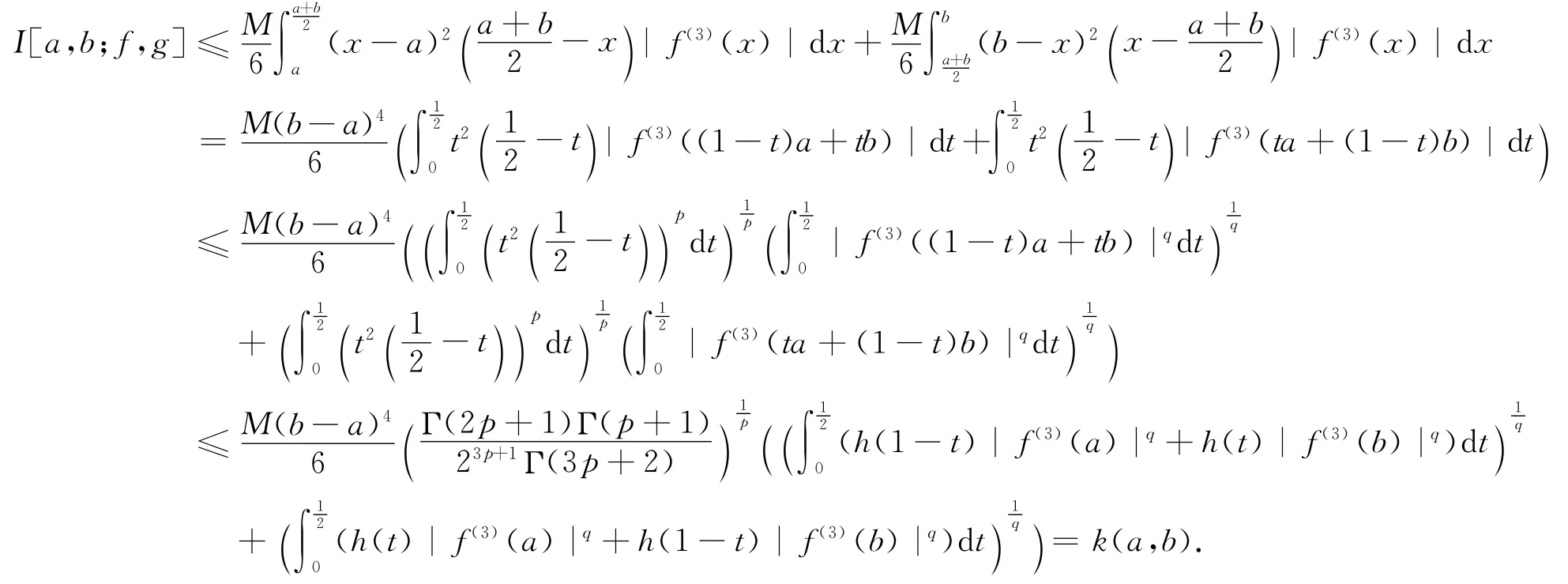
注3 在定理3中，若取g≡1，则可得定理C.

［1］Dragomir S S.On Simpson's quadrature formula for mappings of bounded variation and applications［J］.Tamkang J Math，1999，30（1）：53.

［2］Dragomir S S，Agarwal R P，Cerone P.On Simpson's inequality and applications［J］.J Inequal Appl，2000，5（6）：533.

［3］Liu Z.An inequality of Simpson type［J］.Proc R Soc Lond Ser A Math Phys Eng Sci，2005，461（2059）：2155.

［4］Tseng K L，Yang G S，Dragomir S S.On weighted Simpson type inequalities and applications［J］.J Math Inequal，2007，1（1）：13.

［5］Sarikaya M Z，Set E，Özdemir M E.On new inequalities of Simpson's type for s－convex functions［J］.Comput Math Appl，2010，60（8）：2191.

［6］Liu Zeng.Some sharp modified Simpson type inequalities and applications［J］.Vietnam J Math，2011，39（2）：135.

［7］Özdemir M E，Avci M，Kavurmaci H.Simpson type inequalities for m－convex functions［J／OL］.arXiv：1112.3559v1［math.FA］，15，Dec，2011.

［8］Özdemir M E，Avci M，Kavurmaci H.Simpson type inequalities for functions whose third derivatives in the absolute value are s－convex and s－concave functions［J／OL］.arXiv：1206.1193v1［math.CA］，12，Dec，2011.

［9］Liu Wenjun.Some Simpson type inequalities for h－convex and （α，m）－convex functions［J／OL］.J Comput Anal Appl，2014，16（1）arXiv：1210.4062v2［math.CA］，16，Oct，2012.

［10］Varošanec S.On h－convexity［J］.J Math Anal Appl，2007，326（1）：303.

［11］Sarikaya M Z，Salam A，Yildirim H.On some Hadamard－type inequalities for h－convex functions［J］.J Math Inequal，2008，2（3）：335.

［12］Bombardelli M，Varošanec S.Properties of h－convex functions related to the Hermite－Hadamard－Fejér inequalities［J］.Comput Math Appl，2009（58）：1869.

［13］Sarikaya M Z，Set E，Özdemir M E.On some new inequalities of Hadamard type involving h－convex functions［J］.Acta Math Univ Comenianae，2010，79（2）：265.

［14］Özdemir M E，Gürbüz M，Akdemir A O.Inequalities for h－convex functions via further properties［J］.RGMIA Res Rep Coll，2011（14）：Article ID，22.

［15］Burai P，Hazy A.On approximately h－convex functions［J］.J Convex Anal，2011，18（2）：447.

［16］şcan .Some new general inequalities for h－convex and h－concave functions［J］.Advan Pure Appl Math，2014，5（1）：21.