结构用钢（16Mn）恒载加温试验研究

褚新颖，谢 飞

（1.天津市红桥区消防支队，天津，300131；2.天津市公安消防总队防火部，天津，300090）

0 引言

钢材虽然是不燃材料，但是钢结构本身不耐火，温度大于400℃时，钢材的屈服强度和弹性模量降低幅度较大，在遭受火灾条件下有可能倒塌［1］。钢结构倒塌的原因就是其本身的承载力不足以支撑作用效应［2］。作用效应一般为常数，为确保钢结构安全，则需要保证其承载力大于作用效应才能保证钢结构没有倒塌的危险。而承载力又是材料强度的函数，随着温度的升高，材料强度降低，从而承载力也会减小。由此可见：钢材在高温下的强度直接关系到钢结构建筑的安全问题，故钢材在高温下的强度是建筑结构耐火设计最重要的基础数据之一［3］。

本文采用恒载加温试验方法研究钢材的高温力学性能。恒载加温试验是将承受固定荷载的钢材置于不同温度下，研究钢材的应变－温度－应力关系。钢材的应变－温度－应力材料模型与结构实际受力、升温路径一致，更准确地模拟了钢结构的真实破坏过程。试验目的是通过试验，得到我国生产的钢材的高温力学性能参数的变化规律，建立国产钢材的高温力学性能材质计算模型，为我国制定钢结构抗火设计规范及数据库的建立提供依据。

1 试验方案

1.1 试验设备

本试验设备采用 WAW－1000微机控制电液伺服万能试验机，如图1所示。该试验机是国内具有较高水平的测试设备，采用微机电液伺服方式控制，使用高精度压力传感器、高精度的电子测量、放大器件和液压式夹头，可实现对应力、应变的自动闭环控制，及时实现数据处理和储存。试验机最大加载能力为1000KN，力控制精度为±1%。加热及温度控制系统为微机控制电液伺服万能试验机配备的筒式高温炉及温控仪。炉膛内部高度380mm，均温区长度350mm，试验炉的最高温度可达1000℃，温度控制精度±1℃，到达600℃最大升温时间约10分钟。高温炉热工性能稳定，各温度的升温速率曲线如图2所示。

图1 试验加载加热设备Fig.1 WAW－1000computer control testing machine

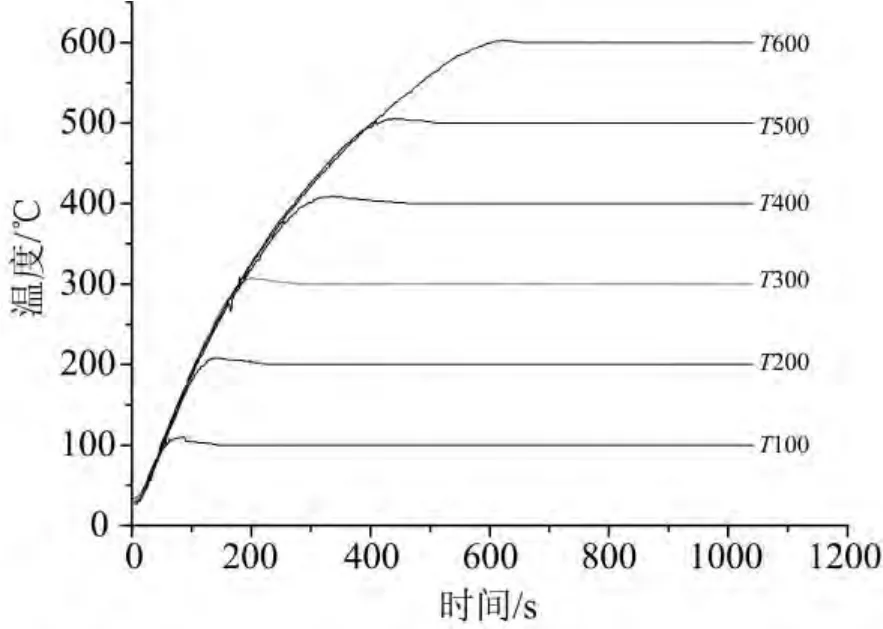
图2 试验炉升温速率曲线Fig.2 The heating rate curve on testing machine

为准确测量试件高温受热部分的变形值，试验采用北京钢铁研究总院定做的电子引伸计，如图3所示。由对称的两部分组成，引伸计框架采用刚性较大的中空铝合金，以免在试验过程中因本身的变形而影响试件变形测量的准确性，为克服试件微弯曲对变形的影响，在引伸计的两个部分各装有一个应变片，而输出的变形值为2个应变片的平均值。引伸计的测量标距500mm，最大量程为25mm，精度0.78%。

1.2 试验材料

试验所用钢材是分别从我国四个钢材生产厂的生产线上直接选取，按照试验设备要求加工成试件进行试验。四个钢厂分别称为JN，SH，XY，NT。试件规格如图4所示。

1.3 试验过程

图3 变形测量电子引伸计Fig.3 The electronic extensometer which measures deformation

图4 试件的形状与尺寸（单位：mm）Fig.4 The size and shape of the steel（unit mm）

恒载升温试验过程为：先建立数据文件，然后将试件置于炉内，夹紧试件上端；密封炉口，安装引伸计；夹紧下端，以0.5KN／s的加载速度加载到预定的荷载水平，保持固定的荷载不变；最后升温到预先设定的温度，并恒温15分钟后停止试验，整个实验过程自动记录试件的变形值。

1.4 变形修正

限于实验设备本身特点，引伸计测量的变形值是500mm范围内的变形值，需要修正为直径为10mm标距为350mm的变形值。为了简化计算，将量测段近似地分成试验温度和变温两个区段，试验温度段长为试验炉均温区长度350mm，变温区段长度为150mm。现假定试件长度范围内的温度分布如图5所示。

试验中，试件两端受荷载应力影响，同时也存在膨胀变形，对试件变形进行修正。

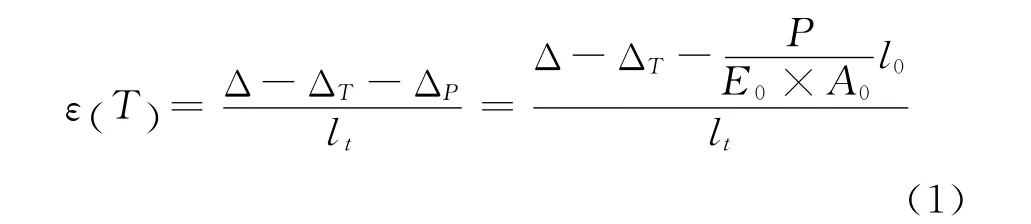
式中Δ—应变仪500mm范围内的变形读数；

ΔP—变温区150mm范围内的荷载变形；

ΔT—变温区150mm范围内的膨胀变形；

P—相对ε（T）时所施加的荷载；

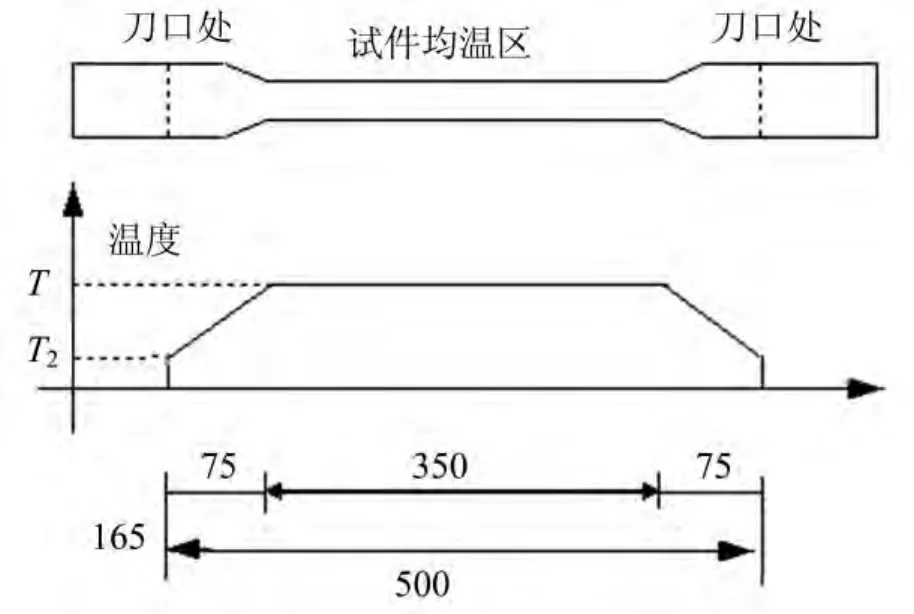
图5 试件长度范围内的温度分布（单位：mm）Fig.5 The temperature distribution in the length range of the steel（unit mm）

E0—钢材的常温弹性模量；

A0—试件变温区段的截面积；

l0和lt—试件变温区段和试验温度区段的长度，分别为固定值150mm和350mm。

而其中试件的膨胀变形ΔT可采用下面计算式进行修正。

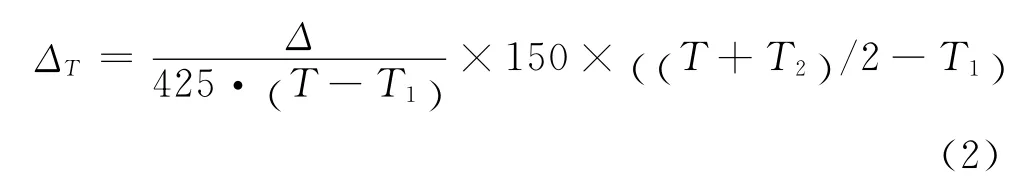
式中，T——试件均温区温度，℃；

T2——恒温后应变仪刀口处温度，℃；

T1——应变仪安装时的环境温度，℃；

2 数据分析处理

2.1 试件变形的分离原则

恒载升温条件下下钢材的变形包括三部分：

一是由热作用产生膨胀变形，是温度的函数；二是由荷载产生的变形，它与材质性质和荷载大小有关；三是耦合变形，与温度和应力都有关。

因此在研究钢材的高温变形过程中，我们把钢材的总变形分为以上三个部分来进行考虑。加载之后受热前由荷载产生初始荷载应变ε0（%），由温度产生热膨胀应变εT（%）和由热－力共同作用所产生的耦合应变εp·T（%），则总应变为：

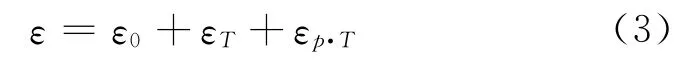
首先通过对四大钢厂钢材进行常温试验，确定出钢材的常温屈服强度和弹性模量，见表1。

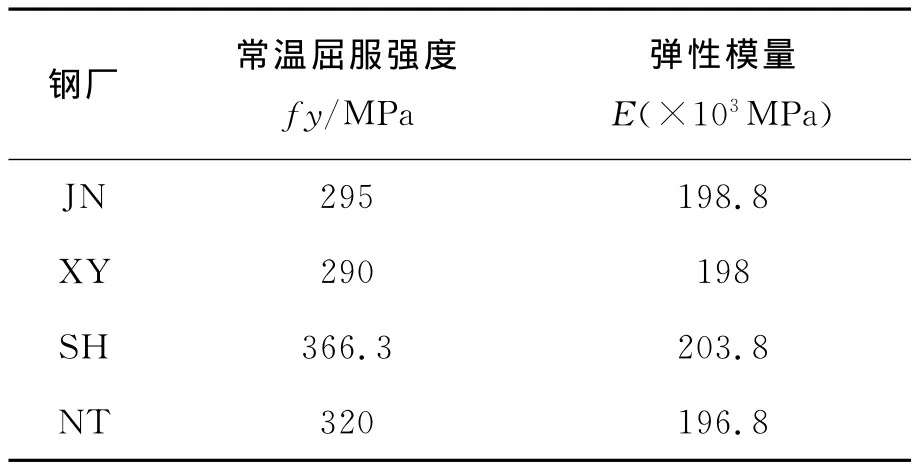
表1 试件的平均常温屈服强度和弹性模量值Table 1 The average yield strength and elastic modulus at room temperature of the steel

再对四个不同钢厂的试件进行恒载升温实验，本实验研究中，温度从200℃到600℃，荷载水平从0.25到0.85之间，一共进行了182次，考虑到安全合理因素，温度水平高的试验荷载水平取低值，温度水平低的试验荷载水平取高值。记录不同试验的温度、应力水平、荷载值、荷载变形、恒温15分钟后的变形，并根据相应的计算依据式（1）和式（2），再计算中间变温区150mm的膨胀变形、恒温区350mm的修正总变形，并计算总应变值。最后对相同温度，相同荷载水平的应变结果进行平均处理，以分析同类钢材的应变－温度－应力之间的内在关系。

2.2 恒载加温总应变规律

各应力水平和温度下精确应变均值汇总于表2，应变均值随应力水平的变化趋势如图6所示，应变均值随温度的变化趋势如图7所示。

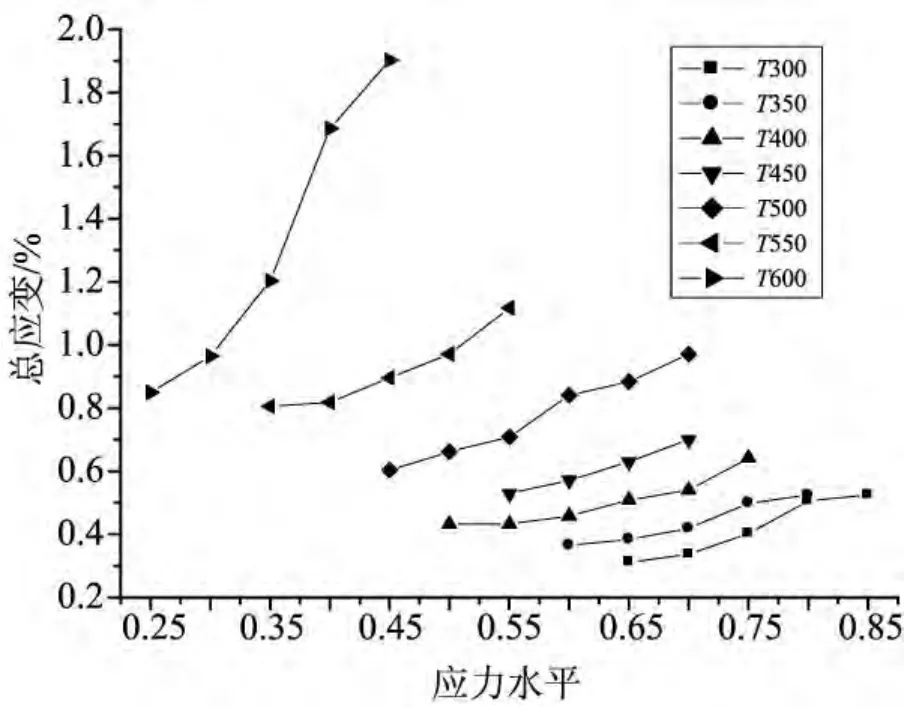
图6 应变均值随应力水平的变化趋势图Fig.6 The change comparison diagram on average strain over stress level

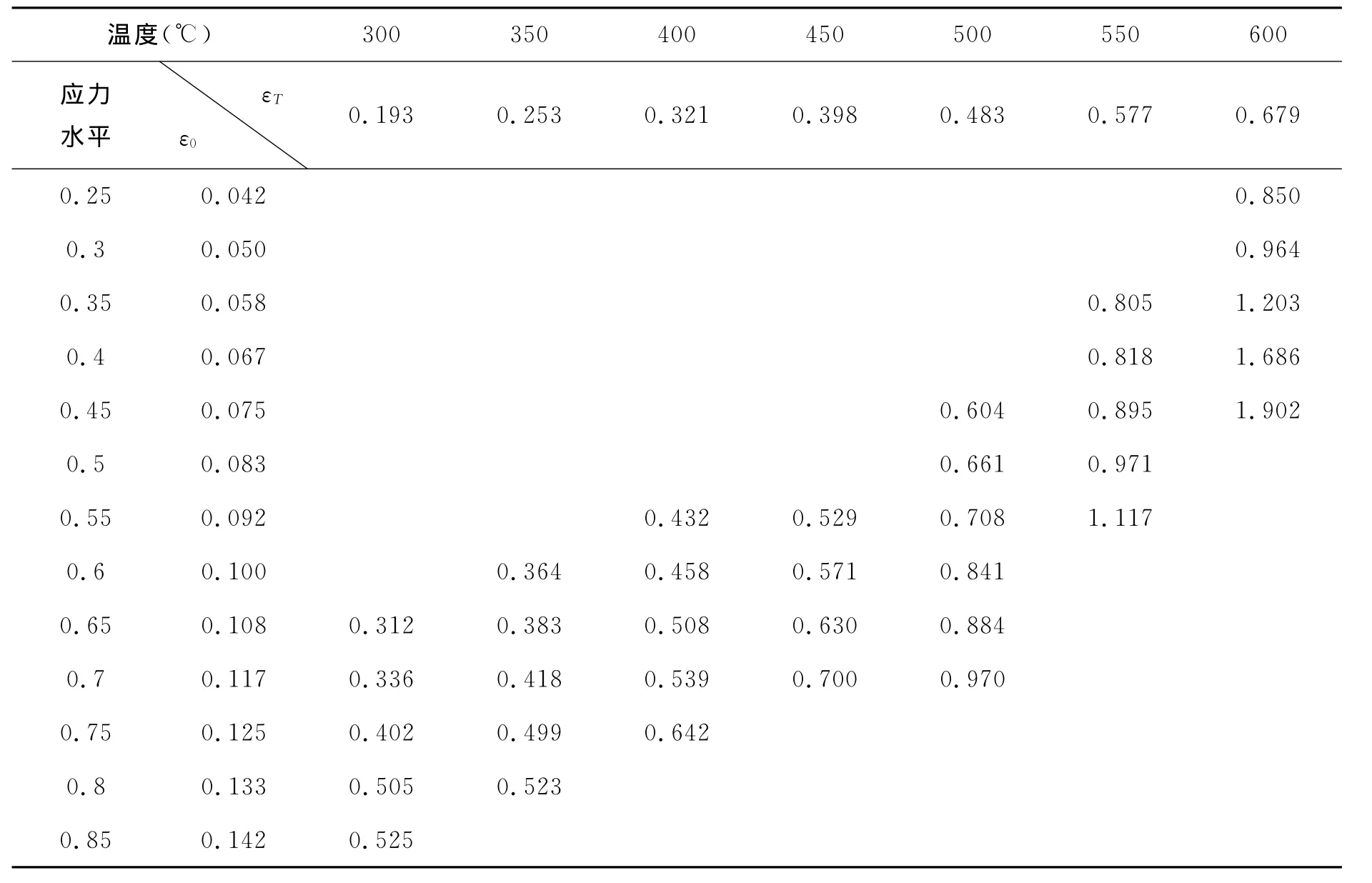
表2 四大钢厂各应力水平和温度下实测总应变均值（%）Table 2 The mean total strain of the steel from four major steelworks at different stress level and temperature

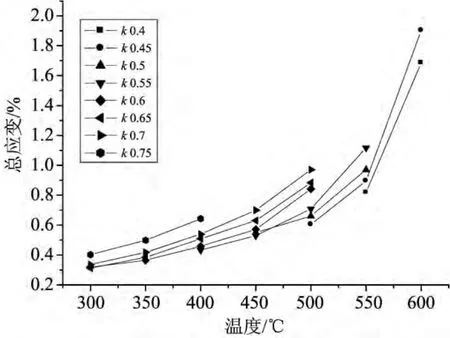
图7 应变均值随温度的变化趋势图Fig.7 The change comparison diagram of average strain over temperature

2.3 荷载应变规律

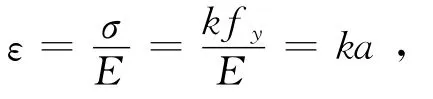
式中k——应力水平

2.4 膨胀应变规律

试件的膨胀应变规律可参考恒载加温实验数据［1］，得出膨胀应变随温度T的变化。

膨胀应变随温度T的变化规律为：

2.5 温度－应力耦合应变规律

根据前面变形处理原则式（3），可以得到恒载升温过程中难以直接测量的耦合应变随温度随荷载水平的变化值。即从总应变中扣除荷载应变ε0和膨胀应变εT后所剩耦合应变列于表3。

分析试验数据发现，应力水平为k，当温度不超过下表数值T0时，只产生初始应变ε0和膨胀应变εT，而不产生耦合应变（此处将耦合应变数值极小情况认为不产生耦合应变，从而建立相应的模型）。将k和T0的关系列于表4。

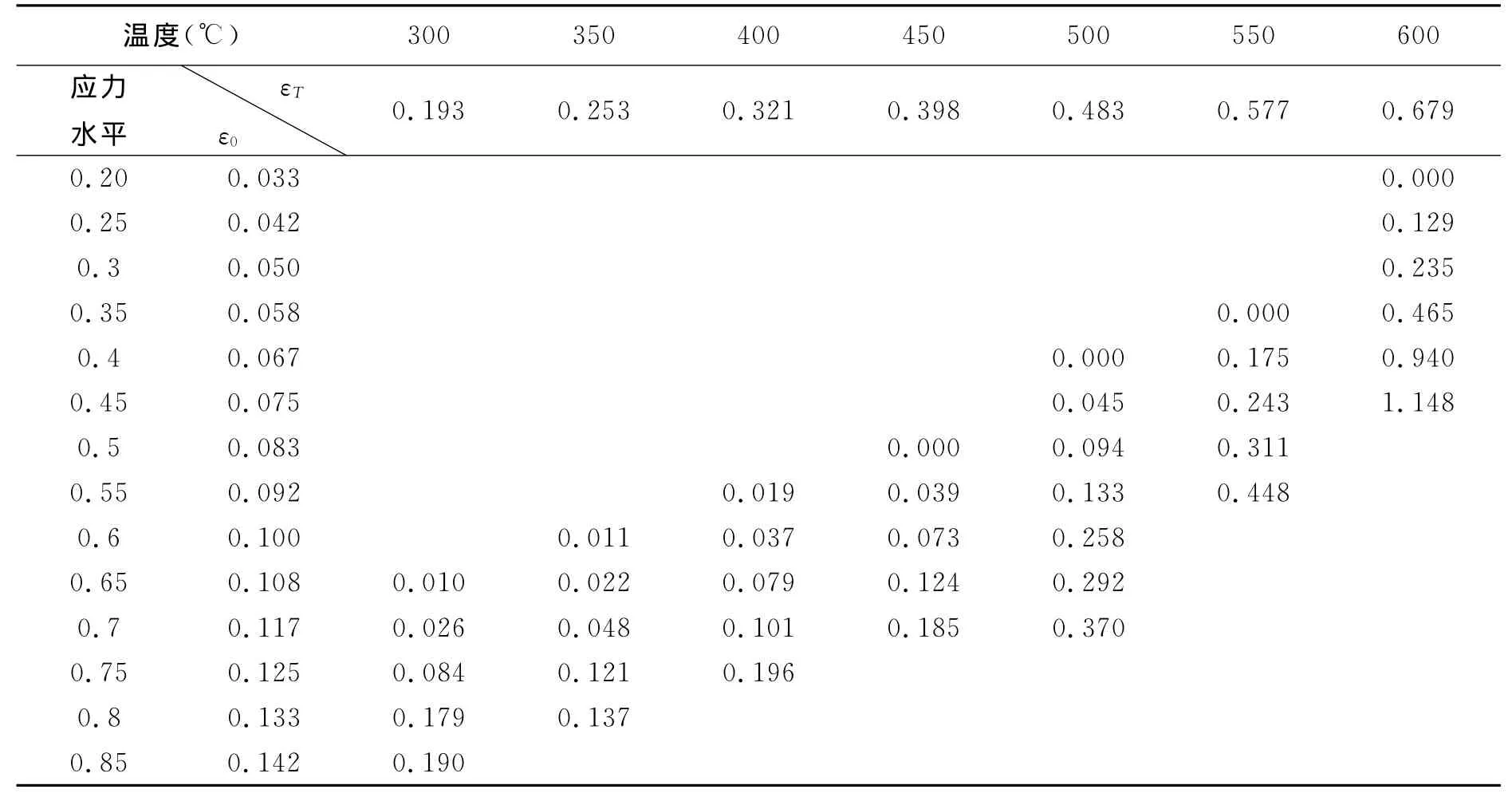
表3 四大钢厂各应力水平和温度下耦合应变均值（%）Table 3 The mean coupling strain of the steel from four major steelworks at different stress levels and temperatures（%）

表4 产生耦合应变的最低温度（℃）Table 4 The lowest temperature on which the coupling strain emerges

对表4中数据进行回归得到：

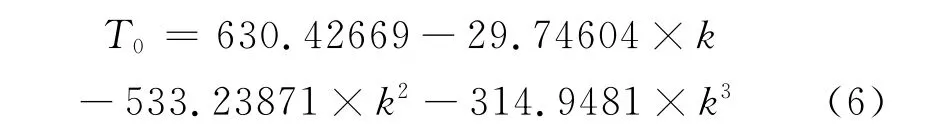
由此也表明，耦合应变值与所受温度和T0之差有关。T－T0数值列于表5。

表5 不同应力水平下T－T0（℃）数值列表Table 5 The list of values T－T0 （℃）under different stress levels

对表3和表5中的数据，进行曲线拟合，可得到下面的统一算式：

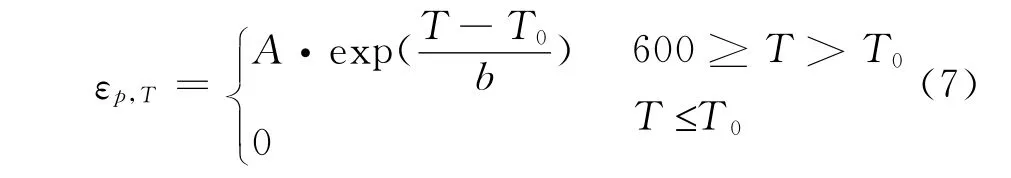
其中，曲线拟合公式（7）所对应的各系数，分别列于表6、表7。

表6 不同应力水平下系数ATable 6 The coefficient A under different stress levels

表7 不同应力水平下系数bTable 7 The coefficient b under different stress levels

可以拟合出系数A和b的回归表达式为

因此，通过总变形的分离，数据回归，得到温度－应力耦合应变具体表达式及相关参数为：

耦合应变：

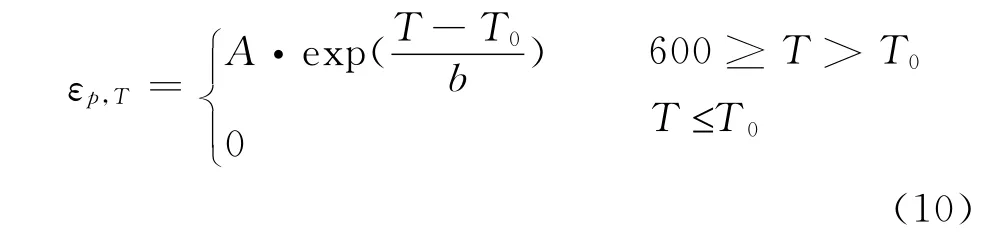
其中A、T0、b分别为前面回归的参数公式（8）、（6）、（9），三个参数均为荷载水平k的函数，荷载水平k取值在0.4～0.75之间，T为温度，℃。

2.6 总应变的公式回归

结合前面的式（3）、（4）、（5）、（10），可以得到总应变回归计算公式：

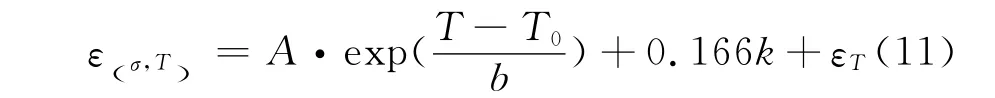
从式（11）不难发现，应变是温度和应力水平的二元函数，也即应变、应力和温度三者是一一对应关系，任意给定其中的两个参数就可以得到第三个参数。总应变随温度和应力的变化规律如图8所示。

2.6 临界温度计算模型

从应变－温度－应力材料模型入手［4－7］，并结合恒温加载的试验结果，可以构建临界温度的计算模型。

利用切线交点法［8］计算出的钢材的强度与0.5%应变对应的强度接近，因此可选择应变0.5%对应的应力水平作为临界荷载对其研究。考虑到恒温加载试验中，应变已经除去膨胀应变，总应变中只包含荷载应变和耦合应变，于是有公式（12）：

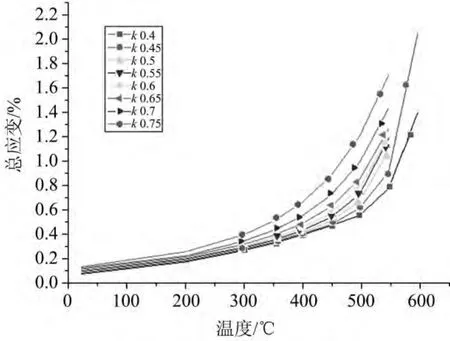
图8 总应变随温度和应力的变化规律Fig.8 The change regulation of total strain over different stress levels and temperatures

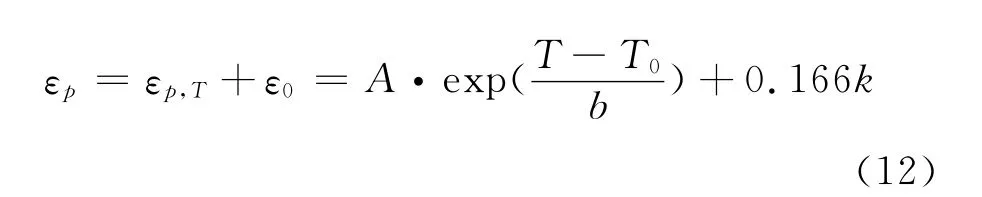
由此推导出钢材温度Ts与应变k的关系为：

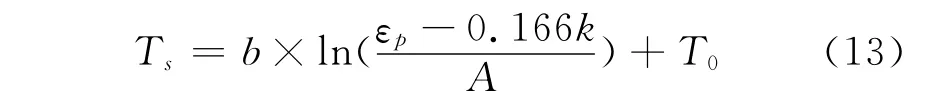
选择应变0.5%对应的应力水平作为临界荷载对其研究（此处εp＝0.5），通过代入公式（13），可以得出临界温度Tc，见表8所示。

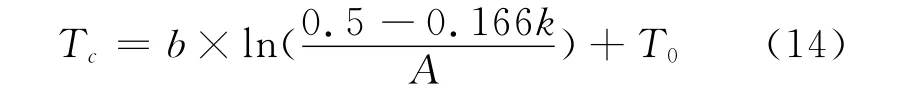
在进行钢结构抗火设计时，往往根据不同的结构和要求选用不同的应变作为屈服应变，若此时能再将温度场确定，那么就可以根据公式确定构件材料在高温下的强度，同时也可根据临界温度确定保护层的厚度，对我国钢结构性能化耐火设计与评估可以提供一定的参考。

表8 不同的应力水平对应的临界温度Table 8 The critical temperatures under different stress levels

3 结论

本文通过对JN，SH，XY，NT四个钢厂生产的16Mn结构钢进行恒载加温试验研究，得到了如下结论：

（1）该类结构用钢材的应变－温度－应力计算模型可以表示为：

以上各式中，k为应力水平，取值在0.4～0.75之间，T为温度，℃。

通过对理论计算值与试验值进行比较，可以发现一致性比较好。

（2）恒载升温试验强度与临界温度计算模型：

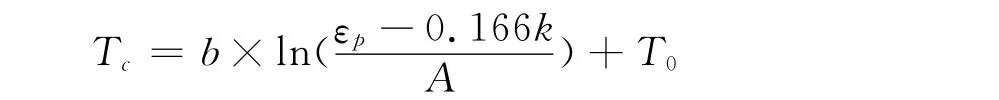
根据此模型，当屈服应变已知时，可由此反推出临界温度，为钢结构保护层厚度计算提供方便，对我国钢结构性能化耐火设计与评估可以提供一定的参考。

［1］陈禄如，刘万忠.中国钢结构行业现状和发展趋势［J］.钢结构，2004，19（2）：31－35.

［2］时虎，等.世贸大楼的倒塌与钢结构防火［J］.消防技术与产品信息，2002，（10）：3－8.

［3］褚新颖，谢飞.结构用刚（16Mn）高温力学性能恒温加载试验研究［J］.火灾科学，2008，17（2）：125－130.

［4］李国强，等.钢柱抗火计算和设计的实用方法［J］.工业建筑，1995，（2）：31－37.

［5］李国强，丁军.耐火钢梁的抗火性能参数分析与抗火设计［J］.钢结构，2003，5（18）：52－55.

［6］屈立军.钢结构火灾时临界温度的计算［J］.建筑技术开发，1994，21（5）：13－16.

［7］李焕群，等.结构用钢的高温试验研究［J］.消防科学与技术，2006，25（6）：11－13.

［8］BSI.Structural use of steelwork in building，Part 8.Code of Practice for Fire Resistance Design［S］.