蛋白质序列的混合特征值对折叠速率的影响
2014-11-14李欣颖白凤兰
李欣颖,白凤兰
(大连交通大学理学院,辽宁 大连116028)
1 材料和方法
1.1 数据
本文从文献[15-18]中选取了83个蛋白质,氨基酸序列从PDB库取得[19]。在选取44个蛋白质中包括13个全α类蛋白质,18个全β类蛋白质和13个混合类蛋白质,以及39个未分类蛋白质。
1.2 蛋白质编码序列的特征值提取
氨基酸的标准化属性Pnorm(i)的计算公式为:
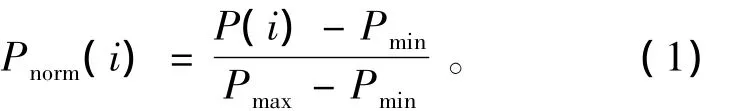
其中,Pnorm(i)是氨基酸的标准化属性,P(i)是氨基酸序列中第i个残基的属性,Pmax和Pmin分别表示氨基酸属性中的最大值和最小值。
蛋白质序列中氨基酸的平均属性Pave的计算公式:
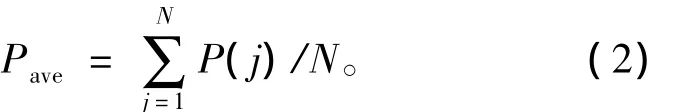
其中,Pave是蛋白质的氨基酸平均属性,P(j)是氨基酸序列中第j个残基的属性,N是氨基酸序列的残基数。
蛋白质序列的复杂度LZc计算公式:
蒙牛在2012年的经营活动中发现到自己在乳制品方面最大的短板就是婴幼儿奶粉,在2012年中国婴幼儿奶粉的市场里,雅士利排第七名,在2012年雅士利拥有5.8%的市场份额,婴幼儿奶粉产品发展已经非常成熟,拥有成熟的技术、产品和市场,蒙牛在扩大自己经营规模的时候,打开了自己在奶粉产品的市场,基本上把自己的缺陷弥补了,同时蒙牛又可以弥补雅士利在企业管理上的不足。蒙牛与雅士利的合并控股是一个双赢的局面,整体的价值都得到了提升。

其中,S表示的是序列,c(S)是序列S的复杂度[11]。
20 个氨基酸 αc、Cα、K0、Pβ、Ra、ΔASA、PI、ΔGhD、Nm、Mu、El属性利用公式(1)计算出标准化后的值。
其中,αc是 α 螺旋的 C 端动力[20-21],Cα是 α螺旋接触面积[15],K0是可压缩性[22-23],Pβ是 β 折叠趋势[21],Ra是在溶剂中的收缩率[24],ΔASA 是溶剂可及表面积[25],PI(at 25℃)表示氨基酸的等电点[26],ΔGhD是吉布斯自由能变性蛋白水化的变化Nm是平均中程接触,Mu是折射率,EL是长距离的非键能[15]。
利用20个氨基酸标准化后的值和公式(2)、(3)计算了13个全α类蛋白质,18个全β类蛋白质和 13 个混合类蛋白质 αc、Cα、K0、Pβ、Ra、ΔASA、PI、ΔGhD、Nm、LZc、Mu、EL 的特征值,以及 39 个蛋白质的 K0、Rα、ΔASA、Mu、El的特征值,由于数据多没列在文章里。
2 结果与讨论
首先,利用多元线性回归函数分别计算了13个全α类蛋白质、18个全β类蛋白质、13个混合类蛋白质和未分类的39个蛋白质的12种特征值与折叠速率之间的相关性,实验值与预测值之间的相关系数分别达到了 0.99、0.96、0.99、0.865,但是用 Jackknife方法检验,都得出p>0.05。由此可知,12种特征值当中某些特征值对蛋白质的折叠速率没有影响,这样经过多次试验,对于全α类蛋白质选取有效特征值Cα、Ra、LZc,对于全 β 类蛋白质选取有效特征值 K0、Pβ、Ra、ΔASA、Nm,对于混合类蛋白质选取有效特征值K0、ΔASA、PI,对于未分类的蛋白质选取有效特征值 K0、Rα、ΔASA、Mu、El,计算这些特征值与折叠速率ln(kf)之间的相关性。
其次,分别对全α类蛋白质、全β类蛋白质、混合类蛋白质和未分类的蛋白质的有效特征值与折叠速率做相关性分析,并与其它方法进行比较。
选取13个全α类蛋白质Cα、Ra、LZc3个特征值与折叠速率ln(kf)做回归方程:

用p值检验了方程(4)每一项特征值,每一特征值对应的p值都小于0.05。实验值与预测值之间的相关系数R=0.89。用Jack-knife方法检验,得出R=0.77、t=4.04、p <0.05。
Gromiha文章中选取了6个全α类蛋白质的1个特征值αc作线性回归,本文在6个数据的基础上增加到13个全α类蛋白质,用特征值αc作线性回归,得到回归方程:
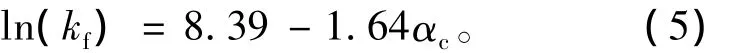
本文用p值检验了得到的方程(5),p>0.05。实验值与预测值之间的相关系数R=0.03,t=-0.097。在选取13个全α类蛋白质的Cα、Ra、LZc3个特征值中,得到回归方程的相关系数为0.89,说明选取的特征值Cα、Ra、LZc对全α类蛋白质有影响。对比结果见表1。

表1 全α类蛋白质回归分析结果Table 1 The results of all-α proteins regression analysis
选取 18 个全 β 类蛋白质的 K0、Pβ、Ra、ΔASA、Nm5个特征值与折叠速率ln(kf)做回归方程:

用p值检验了以上方程的每一项特征值,每一特征值对应的p值都小于0.05。实验值与预测值之间的相关系数R=0.93。用Jack-knife方法检验,得出 R=0.78、t=4.93、p <0.001。
同样18个全β类蛋白质,选取Gromiha文章中的 K0、Pβ、Ra、ΔASA4 个特征值作线性回归,得到方程:

用p值检验了以上方程的每一项特征值,其对应的p值都小于0.05。实验值与预测值之间的相关系数R=0.89。用Jack-knife方法检验,得出R=0.73、t=4.28、p < 0.001。这说明本文选取的特征值 K0、Pβ、Ra、ΔASA、Nm对全 β 类蛋白质有影响。对比结果见表2.
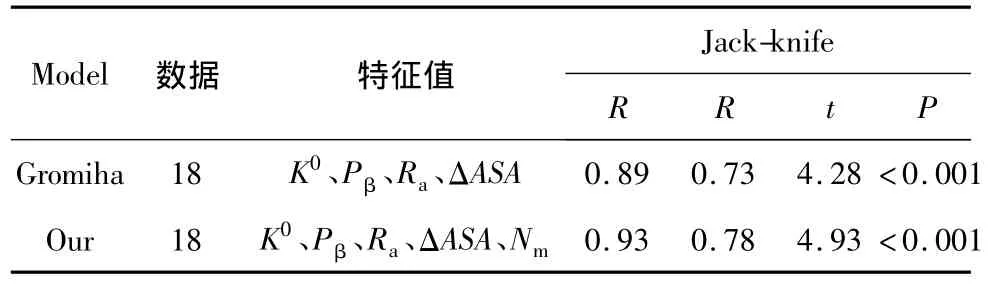
表2 全β类蛋白质回归分析结果Table 2 The results of all-β proteins regression analysis
选取13个混合类蛋白质 K0、ΔASA、PI三个特征值与折叠速率ln(kf)做回归方程:

用p值检验了以上方程的每一项特征值,每一特征值对应的p值都小于0.05。实验值与预测值之间的相关系数R=0.98。用Jack-knife方法检验,得出R=0.97、t=13.46、p <0.001。
同样的13个混合类蛋白质,选取Gromiha文章中的 K0、Ra、ΔASA、ΔGhD4 个特征值作线性回归,得到方程:
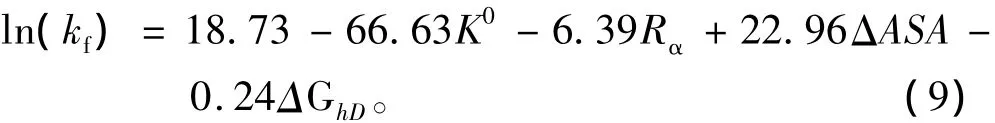
用p值检验了以上方程的每一项特征值,每一特征值对应的p值都小于0.05。实验值与预测值之间的相关系数R=0.96。用Jack-knife方法检验,得出 R=0.91、t=7.07、p <0.001。这说明本文选取的特征值K0、ΔASA、PI对混合类蛋白质有影响。对比结果见表3。

表3 混合类蛋白质回归分析结果Table 3 The results of mixed class proteins regression analysis
对于未分类的39个蛋白质,选取5个特征值K0、Rα、ΔASA、Mu、El与折叠速率 ln(kf)作回归方程:
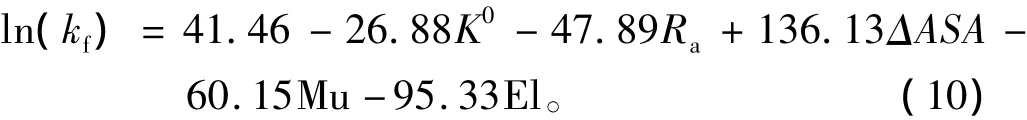
用p值检验了以上方程的每一项特征值,每一特征值对应的p值都小于0.05。实验值与预测值之间的相关系数R=0.86,用 Jack-knife 方法检验,得出 R=0.81、t=8.32、p<0.001。
同样的39个未分类蛋白质,选取Gromiha文章中的K0、Ra、ΔASA、ΔGhD4 个特征值作线性回归,得到方程:
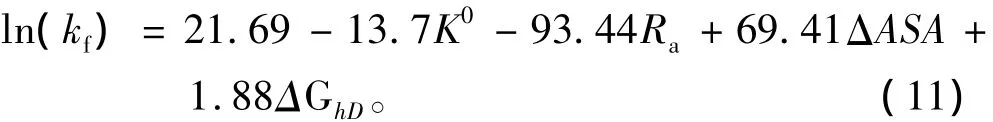
用p值检验了以上方程的每一项特征值,其对应的p值都大于0.05。实验值与预测值之间的相关系数R=0.697。用 Jack-knife 方法检验,得出 R=0.48、t=3.37、p > 0.001。这说明选取的特征值 K0、Rα、ΔASA、Mu、El对未分类蛋白质有影响。对比结果见表4。
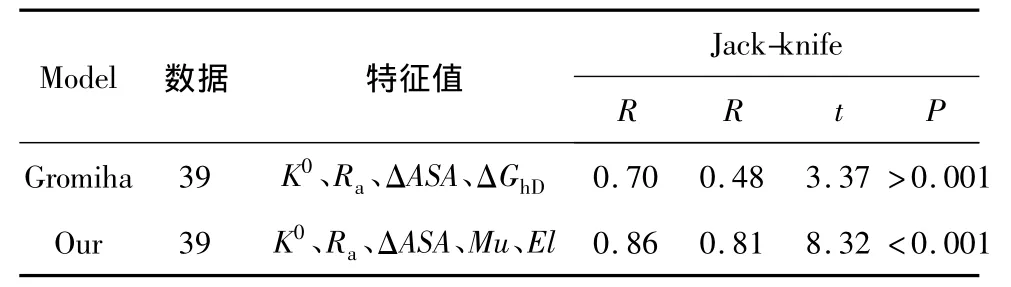
表4 未分类蛋白质回归分析结果Table 4 The results of unclassified proteins regression analysis
通过实验计算得出,对于未分类蛋白质选取5个特征值 K0、Rα、ΔASA、Mu、El计算蛋白质折叠速率预测值,与ln(kf)有良好的相关性。
对于不同类别的蛋白质,其折叠速率有很大的区别。本文研究不同的特征值对不同类别的蛋白质折叠速率的影响,以及特征值对未分类蛋白质折叠速率的影响。从本文的实验结果发现,Cα、Ra、LZc3个特征值对全α类蛋白质折叠有一定的影响,对于全β类蛋白质,在Gromiha文章选取的4个特征值基础上增加了Nm特征值,使得全β类蛋白质的折叠速率有所提高,相关系数达到0.93。为了说明Nm特征值对全β类蛋白质的折叠速率有影响,本文又选取了13个数据进行验证。由实验结果可知,在增加Nm特征值后全β类蛋白质的折叠速率确实有所提高(见表2)。由此可见,增加的特征值是有效特征值。对于混合类蛋白质,本文选取了3个特征值K0、ΔASA、PI其相关系数比Gromiha文章选取特征值得到的相关系数要高(见表3)。由研究结果发现,特征值K0、ΔASA对全β类蛋白质和混合类蛋白质的折叠速率都有影响。选取 K0、Rα、ΔASA、Mu、El5个特征值对未分类的蛋白质的折叠有一定的影响。
3 结论
蛋白质在生物体内占有重要的地位,是一个生物大分子,由20个氨基酸以肽键的形式形成肽链。肽链在空间结构中通过卷曲形成特定的空间结构,如二级结构和三级结构。氨基酸残基及周围介质之间的相互作用决定了蛋白质的结构和折叠速率。由于蛋白质折叠速率对蛋白质功能有一定的影响,近些年来,已有很多方法来预测蛋白质折叠速率。有很多研究工作者从蛋白质的二级结构和三级结构来进行预测蛋白质的折叠速率,但是由于蛋白质的二级结构和三级结构影响因子单一,结构复杂,因此越来越多的研究工作者们开始从蛋白质的一级结构来预测蛋白质的折叠速率。本文就是研究蛋白质的一级结构信息对蛋白质折叠速率的影响,运用生物统计学和生物信息学的方法,选取了蛋白质编码序列的一些特征值,通过实验验证了这些特征值对不同类别的蛋白质折叠速率的影响不同。
本文对于全α类蛋白质,全β类蛋白质,混合类蛋白质和未分类蛋白质分别得到4个线性回归方程。利用这些回归方程研究了所选取的特征值与蛋白质折叠速率之间的相关性,得到了较好的结果,比Gromiha文章选取的特征值相关系数都有所提高。不同的数据集对结果有一定的影响,如何减少数据集对结果的影响会在后续工作中进行更深入研究。
References)
[1] GUO Jianxiu,MA Binguang,ZHANG Hongyu.Progress in protein folding rate prediction[J],Acta Biophysica Sinica,2006,22(2):89 -95.郭建秀,马彬广,张红雨.蛋白质折叠速率预测研究进展[J],生物物理学报,2006,22(2):89-95.
[2] GROMIHA M M,SELVARAJ S.Bioinformatics approaches for understanding and predicting protein folding rates[J].Current Bioinformatics,2008,3(1):1-9.
[3] PLAXCO K W,SIMONS K T,BAKER D.Contact order,transition state placement and the refolding rates of single domain proteins[J].Journal of Molecular Biology,1998,277(4):985-944.
[4] ZHOU H,ZHOU Y.Folding rate prediction using total contact distance[J].Biophysical Journal,2002,829(1),458-463.
[5] GONG H,ISOM D G,SRINIVASAN R,et al.Local secondary structure content predicts folding rates for simple two-state proteins[J].J Mol Biol,2003,327(5):1149-1154.
[6] IVANKOV D N,FINKELSTEIN A V.Prediction of protein folding rates from the amino acid sequence-predicted secondary structure[J].Proc Nat Acad Sci USA,2004,101(24):8942-8944.
[7] SHAO H,PENG Y,ZENG Z H.A simple parameter relating sequences with folding rates of small helical proteins[J].Protein Pept Lett,2003,10(3):277 -280.
[8] GALZITSKAYA O V,GARBUZYNSKIY S O,IVANKOV D N,et al.Chain length is the main determinant of the folding rate for proteins with three-state folding kinetics[J].Proteins,2003,51(2):162 -166.
[9] 徐宏睿,马彬广.蛋白质折叠速率决定因素与预测方法的研究进展[J],生物物理学报,2013,29(3):192-202.XU Hongrui,MA Binguang.Progress in the study on determinants of protein folding rate and method of folding rate prediction[J].Acta Biophysica Sinica,2013,29(3):192-202.
[10] MA B G,GUO J X,ZHANG H Y.Direct correlation between proteins'folding rates and their amino acid compositions:an ab initio folding rate prediction[J].Proteins,2006,65(2):362 -372.
[11] HUANG J T,XING D J,HUANG W.Relationship between protein folding kinetics and amino acid properties[J].Amino Acids,2012,43:567 -572.
[12] GROMIHAM M,THANGAKANI A M,SELVARAJ S.FOLD-RATE:prediction of protein folding rates from amino acid sequence[J].Nucleic Acids Res,2006,34(suppl_2):70-74.
[13] HUANG L T,GROMIHA M M.Analysis and prediction of protein folding rates using quadratic response surface models[J].J Comput Chem,2008,29(10):1675 -1683.
[14] GOU J X,RAO N N,LIU G X,et al.Predicting protein folding rate from amino acid sequence[J].Prog Biochem Biophys,2011,37(12):1331 -1338.
[15] GROMIHA M M.A statistical model for predicting protein folding rates from amino acid sequence with structural class information[J].Chem Inf Model,2005,45(2):494-501.
[16]于志芬,李瑞芳.同义密码子的使用偏好性对蛋白质折叠速率的影响[J],生物物理学报,2013,29(8):603-613.YU Zhifen,LI Ruifang.The influence of synonymous codon bias on protein folding rates[J].Acta Biophysica Sinica,2013,29(8):603 -613.
[17]胡睿,史小红,李晋惠.基于序列疏水值震荡的折叠速率预测[J].生物信息学,2013,11(2):86 -89.HU Rui,SHI Xiaohong,LI Jinhui.Prediction of protein folding-rate based on the hydrophobic value vibration[J].Chinese Journal of Bioinformatics,2013,11(2):86 -89.
[18]胡睿,史小红,基于残基接触数的蛋白质折叠速率预测[J].西安工业大学学报,2013,33(2):146 -150.HU Rui,SHI Xiaohong.Prediction of protein folding-rate based on the residues contact numbei[J].Journal of Xi’an Technological University,2013,33(2):146 -150.
[19] BEMAN H M,WESTBROOK J,FENG Z,et al.The protein Databank[J].Nucleic Acids Res,2000,28(1):235-242.
[20]GROMIHA M M,SARAI O A.Important amino acid properties for enhanced thermostability from mesospheric to hemophilic protein[J].Biophys Chem,1999,82:51 -67.
[21] CHOU P Y,FASMAN G D.Prediction of the secondary structure of proteins from their amino acid sequence[J].Adv Enzym,1978,47:45 -148.
[22] IQBAL M,VERRALL R E.Implications of protein folding.Additivity schemes for volumes and compressibilities[J].Biol Chem,1988,263(9):4159 -4165.
[23]GEKKO K,NOGUCHI H.Compressibility of globular proteins in water at 25 degree C[J].Phys Chem,1979,83(21):2706-2714.
[24] PONNUSWAMY P K,PRABHAKARAN M,MANAVALAN P.Hydrophobic packing and spatial arrangement of amino acid residues in globular proteins[J].Biochim Biophys Acta,1980,623(2):301 -316.
[25] OOBATAKE M,OOI T.Hydration and heat stability effects on protein unfolding[J].Prog Biophys Mol Biol,1993,59(3):237 -284.
[26]李丹,基于蛋白质图形表示的膜蛋白跨膜区预测[D].杭州:浙江理工大学,2012.LI Dan.The prediction oftransmembrane domains based on the graphical representation of protein sequences[D].HANG zhou:Zhejiang Sci-Tech University,2012.
