参照群与群间相对剥夺：理论与实证

任国强，尚明伟，潘秀丽

（1.南开大学 经济研究所，天津300071；2.天津理工大学 管理学院，天津300384）

一、引 言

相对剥夺一词最先出现在Stouffer等（1949）的一篇文章中，他将一个人与比他成功的其他人比较时产生的失落感称为相对剥夺，但是他既没有给出剥夺正式的定义，也没有给出具体测量方法。Runciman（1966）对相对剥夺做出了更加精确的描述，将相对剥夺定义如下：一个人感到剥夺要满足四个条件：（1）他没有X；（2）其他人在过去或者未来可以预期的某个时间里可以得到X；（3）他有得到X的欲望；（4）他认为他理应得到X。

自从Runciman给出相对剥夺概念以来，对相对剥夺的研究便成为社会科学领域内一个非常重要的研究课题，这些研究可以划分为两个层面：一个是如何测度相对剥夺；另一个是相对剥夺对其他产出变量的影响。这些产出变量可以分为四类（J.Smith等，2011）：（1）集体行为，主要包括社会冲突和暴乱等；（2）群间态度，包括政治政策、移民、对外来人员的偏见和对内部人员身份的认同等；（3）个体有导向的行为，包括行为不良、旷工、酗酒、腐败和犯罪等；（4）对个体身心健康、沮丧与焦虑和自我评价的内部反映。国内有些学者虽然对这些变量进行了研究，但是大多采用的是群体不平等指标，例如基尼系数等，但是用群体不平等指标可能会掩盖微观水平的诱因，尽管基尼系数可以看作是相对剥夺指数——Kakwani指数的加总，但是在实证分析时使用基尼系数做自变量会使相对剥夺较低的个体和相对剥夺较高的个体忍受不平等带来的相同的负面影响，这一点无论从理论上还是直觉上都是站不住脚的，因此，微观水平的分析只能采用微观的不平等指标——个体相对剥夺指数，而研究不平等的变动趋势、区域间和群体间不平等的比较等宏观层面，则应采用加总后的相对剥夺指数——不平等指数。科学合理的相对剥夺测度指标对于研究相对剥夺对其他产出变量的影响有着至关重要的意义，可以影响其显著性和影响程度，进而影响相关政策的制定。目前比较有代表性的相对剥夺测度为：Yitzhaki指数、Kakwani指数、Podder指数和Esposito指数。Yitzhaki（1979）最早给出了相对剥夺的测度模型，他把收入作为测度相对剥夺的变量，认为群内只要存在比该个体收入高的个体，那么该个体就会感到被剥夺，大小用相应的收入差距进行度量，该个体在群内所感到的相对剥夺为这些差距的加总再除以该群的样本数，Yitzhaki还证明所有个体剥夺的加权平均等于绝对基尼系数；Kakwani（1984）、Chakravarty（1997）和Deaton（2001）等学者则认为个体在一个群内的相对剥夺应该等于Yitzhaki指数除以该群的收入均值，Kakwani还给出了一种图形化工具——相对剥夺曲线，该曲线以分位数为横坐标（收入按升序排列），该份额所对应个体的相对剥夺为纵坐标，相对剥夺曲线和两个坐标轴围成的图形的面积等于基尼系数；Podder（1996）认为某个个体和收入比其高的其他个体比，所受到的相对剥夺大小应该用收入对数的差距进行度量，该个体在群内所感到的相对剥夺为这些差距的加总再除以该群的样本数；Esposito（2010）认为个体i和收入比他高的个体j相比，其感到的相对剥夺等于个体j与个体i的收入之差再除以个体j的收入，在群内所感受到的相对剥夺为上述剥夺的加总再除以该群的样本数，和其他三个指数相比，Esposito指数才是真正意义上的相对剥夺测度。无论采用何种测度对象，也不论采用哪种指数，经过计算后得到的个体相对剥夺指数可以被认为是一种客观存在，而不再是主观感受，但是这两者之间还是有着显著的关联关系，例如D’Ambrosio等 （2007）的实证分析结果表明相对剥夺和收入的主观满意度之间有着显著的负相关关系。上述四个指数均是以全体社会成员作为参照群进行研究的，没有对参照群的概念给予足够的关注。

但是，个体间进行收入比较时，一个人往往是和与其具有某些共同特征的人比较，而不一定是一个社会的所有个体。Silber和Verme（2010）认为在评价一个人在社会中的状况时，该个体把他自己和所处环境与其类似的个体进行比较，这里的环境，不仅指Frank（2007）所说的“居住环境”，还可以是一个个体的“职业环境”或他的“家庭环境”（背景）等其他方面。总之，一个群体所共有的一些特征都可以用来作为确定参照群的标准，这种特征可以是种族、性别、教育水平（Eibner和Evans，2004），也可以是种族、年龄、社会阶层、宗教信仰、政治价值观以及地理区域（Bylsma和Major，1994）等。此外，Ferrer－i-Carbonell（2005）认为和某个个体年龄相近、教育程度类似并且居住在同一区域内的群体可以作为其参照群。

目前相对剥夺的研究主要集中在群内的相对剥夺，当考虑一个个体在其所在的某个参照群内的相对剥夺时，学术界通常采用两种方法：一是把现有的以全体社会成员为参照群的相对剥夺指数应用于该参照群，不同的是该参照群中的个体比较的对象是该参照群中收入比他高的个体，而不是全体社会成员中收入比他高的个体；二是建立集成参照群的相对剥夺指数，这方面开创性的工作可归功于Ebert和Moyes（2000），他们假设任何一个人口的子集均可以作为一个参照群，该参照群中收入高于研究个体收入的所有个体构成比较群，在此基础上建立了集成参照群的相对剥夺模型，并探讨了其满足的公理化特征；Bossert和D’Ambrosio（2006）对参照群和比较群的定义做了明确的界定，他们认为参照群包括所有和该个体比较的成员，而比较群则是这些成员中收入较高的群体构成的子集，在参照群被固定和整个社会给定的条件下，在一个统一的框架内给出了Yitzhaki指数的公理化特征，弥补了Ebert和Moyes（2000）方法的不足；Silber和Verme（2010和2012）也尝试在测度相对剥夺时集成参照群的思想。

但是在现实中一个人感受到的剥夺不仅来自自己所在的参照群内部，也来自于和其他群体的比较，例如蓝领和白领的比较、农村居民和城镇居民比较、非垄断行业员工和垄断行业员工的比较等。Runciman（1966）也没有把相对剥夺的概念局限于一个参照群内，他认为一个个体本身属于一个群，但是进行比较的却可能是另外的群。但是，到目前为止对不同群间相对剥夺研究的文献却比较稀少，Martín和Olmedo（2007）把Yitzhaki指数推广到不同群之间，并把一个群内的绝对剥夺分解为子群内部和子群间绝对剥夺的加总；洪兴建（2008）在研究基尼系数子群分解时也曾给出了群间相对剥夺的测度公式；任国强等（2011）采用推广Kakwani指数的方法，克服了洪兴建（2008）的缺陷。

尽管群间的相对剥夺已经有了一定的研究进展，但仍在以下方面有待进行改进。首先，现有研究没有把参照群的思想集成到群间剥夺的测度模型中，造成群内剥夺测度和群间剥夺测度分别是在不同的框架下进行，没有形成统一的分析框架；其次，已有研究只是解决了群间剥夺测度的一个方面，即构造一个群间剥夺测度，然后分析该测度的性质，没有给出一个函数满足哪些公理就是我们给出的群间剥夺测度的证明，即只证明了群间剥夺测度充分必要条件中的必要条件；再次，现有群间剥夺的出发点都是基尼系数的子群分解，偏重于群内剥夺和群间剥夺形式的一致性、群间剥夺的正规性和是否为真正意义上的加权平均等方面，但是群间剥夺除了应用于基尼系数子群分解外，还有一个重要的目的是研究降低群间收入差距的措施，从而提出科学的、可操作性的政策建议，因此有必要对加总后的群间剥夺的性质进行进一步深入研究。

本文的主要目的是把Kakwani方法扩展到不同的群体，使不同群体间的个体能够进行比较。这样就能够获得属于某个群的个体相对于另一个群中所有个体的相对剥夺，进一步可得到一个群相对于另一个群的相对剥夺，并可深入分析群间剥夺的性质，而Kakwani指数只是两个群的收入变量具有相同分布情况下的一个特例。群内和群间的个体剥夺可应用于确定相对剥夺对诸如健康、迁移、不良习惯和消费等指标的影响，而群间相对剥夺则是分析降低群间收入差距的一个重要工具。本文在已有研究的基础上，首先通过构造一个个体在另一个群中的比较群，建立集成参照群思想的相对剥夺测度的统一分析框架，得到个体绝对剥夺测度，分析了该个体绝对剥夺测度满足的一系列性质，并证明如果一个函数满足聚焦性公理、加和可分解性公理、平移不变性公理、线性齐次性公理和正规化公理，则该函数就是我们给出的个体绝对剥夺测度，在此框架下现有的群内相对剥夺只是个体所在群和参照群相同时的一个特例；其次，在个体绝对剥夺测度的基础上，我们得到了个体相对剥夺测度，通过拓展Kakwani理论，绘制了不同群间的相对剥夺曲线；再次，在前面研究的基础上进一步给出加总后的群间相对剥夺的性质；最后，利用CGSS2008数据进行了实证分析。

二、参照群、群间个体绝对剥夺及其公理化特征

（一）符号说明。设R（R＋）代表所有的实数（正实数）。为每个分量均为正值的n维向量空间，In是n维单位向量。设X、Y是两个群，样本数分别为，这两个群对应的收入向量分别为其中xi，yj分别为X中个体i和Y中个体j的收入，i∈N，j∈M，我们假设对于Y中任何一个个体k，其参照群为X，其比较群为X中收入高于yk的个体，则Bk（x）＝Bk（X）＝即为Y中个体k的比较群。我们令Min（Y）为群Y中的最低收入，Max（X）为群X中的最高收入，则为X中收入比Y中最低收入还要低的个体构成的集合是Y中收入比X中最高收入还要高的个体构成的集合。任给，N的一个子集K，向量x的定义如下：

对于任意i∈N，有

（二）集成参照群的群间个体绝对剥夺测度及其性质。根据Runciman（1966）、Yitzhaki（1979）和任国强等（2011）的相关定义，我们给出属于不同群的两个个体间的剥夺的定义。

定义1：设X、Y是两个群，xi是X中个体i的收入，yk是Y中个体k的收入。则X中个体i对Y中个体k的剥夺为：

由定义可得，如果xi＞yk，则X中个体i对Y中个体k的剥夺为xi-yk，否则为0。

由于X是群Y中个体k的参照群，个体k和群X中收入高于他的个体相比都会产生剥夺，根据已有文献的通常做法，计算群X中每个个体与Y中个体k的剥夺，并对群X中的所有个体求和，然后除以群X的样本数n，得到群X对群Y中个体k的绝对剥夺AD（x，yk）为：

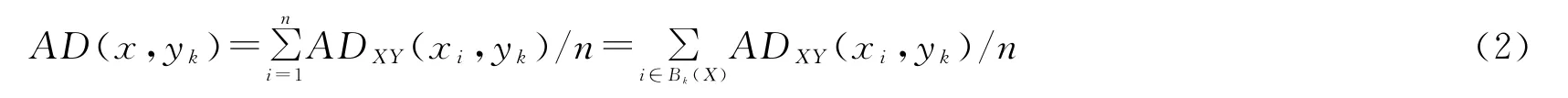
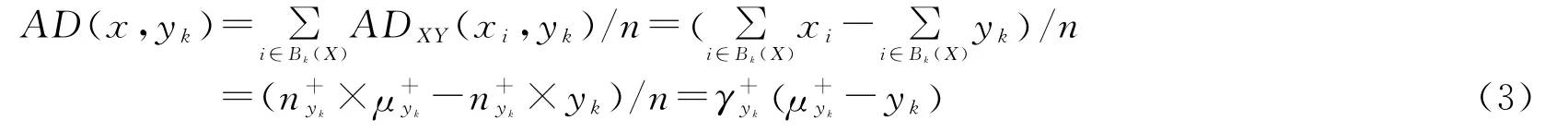
根据公式（3），我们可以很容易地求出群X对群Y中任何一个个体的绝对剥夺。

群X对群Y中个体k的绝对剥夺AD（x，yk）是群X的收入分布x和群Y中某个个体收入yk的函数，它具有如下性质：

性质1：①证 明见任国强（2011），Martín和 Olmedo（2007）。在x保持不变的条件下，AD（x，yk）是群Y中收入的严格递减函数，即对任意k，l∈M，如果yk＞yl，则AD（x，yk）＜AD（x，yl）。

性质2：②证明见Martín和Olmedo（2007），在其证明中，采用的是连续的收入分布，AD（x，yk）对yk的二阶导数等于yk在X中的密度函数，所以大于0，即在x保持不变的条件下，AD（x，yk）是群Y中收入的严格凹函数。在x保持不变的条件下，AD（x，yk）是群Y中个体收入的严格凹函数。

性质3：AD（x，yk）是非负的，如果群Y中某个个体的收入比X中的最高收入都高，则群X对该个体的剥夺为0。

因为对任意一对xi和yk，ADXY（xi，yk）都≥0，所以AD（x，yk）是非负的。如果MaxY（X）≠Φ，即至少存在一个k∈M使得yk∈MaxY（X），则对X中任意一个个体i的收入xi，都有xi＜yk，所以ADXY（xi，yk）＝0，1≤i≤n；进而可得AD（x，yk）＝0。

性质4：AD（x，yk）只与X中收入高于yk的个体有关，与低于yk的个体无关。

性质4在很多文献中被称为焦点（Focus）公理，其严格数学意义的表述如下：任给两个样本数为n的群X、Z，其收入分布为如果＝Bk（Z），且对于i∈Bk（X）都有yi＝zi，那么就有AD（x，yk）＝AD（z，yk）。

性质5和性质6说明X中个体收入的变化如何影响AD（x，yk）。

性质5：群X中收入高于yk的任何一个个体收入的增加，都会使AD（x，yk）增加；X中收入高于yk的任何一个个体收入的减少，都会使AD（x，yk）减少。

性质6：群X中收入低于yk的任何一个个体收入的增加，只要增加后的收入不超过yk，AD（x，yk）就不变；X中收入低于yk的任何一个个体收入的减少，AD（x，yk）都不变。

性质7和性质8说明群X中个体的收入转移对AD（x，yk）的影响。

性质7：群X中收入高于yk的两个个体间的收入转移，只要转移后两个个体的收入仍都高于yk，则AD（x，yk）不变；群X中收入低于yk的两个个体间的收入转移，只要转移后两个个体的收入仍都低于yk，则AD（x，yk）不变。

性质8：群X中收入高于yk的个体向收入低于yk的个体进行收入转移，AD（x，yk）减少。

性质9和性质10说明如果群X中所有个体的收入和群Y中个体k的收入yk，都发生同一程度的变化，AD（x，yk）如何变化。

性质9：如果群X中所有个体i的收入xi和群Y中个体k的收入yk都增加一个相同的数值，则AD（x，yk）不变。

性质9在很多文献中被称为平移不变性（Translation invariance）公理，Bossert和D’Ambrosio（2006）给出的严格数学意义的表述如下：对所有使得成立的，都有AD（x＋δ×In，yk＋δ）＝AD（x，yk）。

因为对群X中任何一个个体i，都有ADXY（xi＋δ，yk＋δ）＝ADXY（xi，yk），所以性质9成立。但是，如果δ∈R为负值，那么可能存在，使得x＋δ×In的某些分量小于0，不满足其的假设，因此，上述平移不变性公理是有条件限制的，为了使平移不变性公理对所有都成立，我们对Bossert和D’Ambrosio（2006）的不变性公理进行了如下扩展：

因为对群X中任何一个个体i，如果xi＞yk，则xi＋δ＞yk＋δ，此时ADXY（xi＋δ，yk＋δ）＝ADXY（xi，yk），如果xi＜yk，则不管zi＞0或zi＝0，都有zi＜yk＋δ，所以ADXY（zi，yk＋δ）＝0，而此时ADXY（xi，yk）＝0，所以有AD（x＋δ×In，yk＋δ）＝AD（x，yk），也就是AD（z，yk＋δ）＝AD（x，yk）。

性质10：①性质10在很多文献中被称为线性齐次性（Linear homogeneity）。如果群X中所有个体的收入和群Y中个体k的收入都按同一比例变化，则AD（x，yk）也按同一比例变化。即对任意，λ∈R＋有

（三）群间个体绝对剥夺的公理化特征。集成参照群思想的个体绝对剥夺测度模型研究文献主要有二，一是Ebert和 Moyes（2000）给出，二是Bossert和D’Ambrosio（2006）给出。两者的一个重大区别就是参照群选取不同，由此带来的个体绝对剥夺的公理化特征无论是个数还是内涵都有很大的区别。Bossert和D’Ambrosio（2006）认为对其选择的参照群，个体独立性和匿名性并非需要，加和可分解性的内涵也大有不同，加和可分解性是一种分离性质，Ebert和Moyes（2000）称之为加性分解，其假定在收入分配保持不变的情况下，如果参照群被分为两个子群，则相对于该参照群的个体绝对剥夺等于相对于被分解成的两个子群的个体绝对剥夺的加总。显然，如果参照群是固定的而且是由整个社会给出的，除了退化的情况外，加性公理是不成立的。Bossert和D’Ambrosio（2006）的解决办法是：如果一个个体k的比较群被分为两个子群，则由原先的收入分配可以得到两个新的收入分配，令这两个收入分配中属于其他子群的个体的收入都等于个体k的收入yk，其他收入不变，然后对这两个收入分配应用可加性。他们的做法虽然存在一定的合理性，但是其将收入分配中属于其他子群的个体的收入强行改为yk的做法，缺乏科学依据。

那么，如何定义加和可分解性公理才合理呢？我们试图先对AD（x，yk）满足的分解性质进行分析，然后通过分析得到的公式，反过来定义加和可分解性公理。

考虑个体绝对剥夺的公理化特征时，有一个公理是必须包含的，这个公理就是正规化公理。本文采用的正规化公理和Bossert和D’Ambrosio（2006）的类似，但是由于本文考虑的是不同群间的相对剥夺，因此对被参照的个体要明确指定其收入为0。进而本文使用的正规化公理如下：对于收入分配x，当存在个体j使得xj＝1且对任意i∈N，i≠j都有xi＝0时，AD（x，0）＝1／n。有了上述准备，我们可以得到如下定理：

定理1：一个个体剥夺指数D（x，yk）满足聚焦性公理、平移不变性公理、线性齐次性公理、正规化公理及加和可分性公理的充分必要条件是D（x，yk）＝AD（x，yk）

证明：当D（x，yk）＝AD（x，yk）时，很容易可证该指数满足以上公理。反向证明如下：

假设D（x，yk）是满足以上公理化特征的个体剥夺指数，考虑如下分布 （xjIn，其中xj＞yk，即该分布中除了第j个个体外，其他个体的收入都为0，即根据平移不变性公理，令δ＝-yk则有：

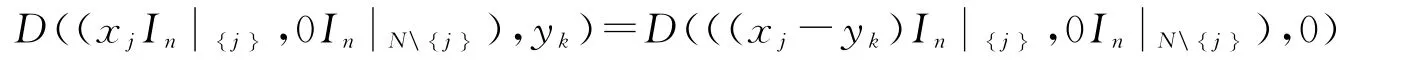
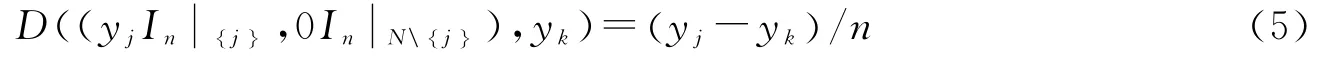
个体绝对剥夺指数尽管有很多良好的性质，但也有很多缺点：（1）由于个体绝对剥夺没有一个明确的范围界限，我们很难根据一个个体绝对剥夺的数值对其剥夺程度给出一个明确的评价；（2）个体绝对剥夺指数是有量纲的，而且取值不在［0，1］，因此不能用于多维剥夺的加总过程；（3）个体绝对剥夺不仅对样本数目敏感，也对收入规模敏感，例如所有样本的收入增加一倍，个体的绝对剥夺也增加一倍，这一点明显与实际的经验不符，当把个体绝对剥夺指数应用于不同社区、不同时间比较时，这一点尤其要引起注意（Eibner和Evans，2005；Lhila和Simon，2010）。因此，有必要在个体绝对剥夺指数的基础上，得到性质更佳的相对剥夺测度。

三、群间个体相对剥夺测度及相对剥夺曲线

（一）个体相对剥夺测度的定义和性质。

证明：∀j∈Bk（x），都有xj-yk≤xj，当且仅当yk＝0时等号成立，所以ADx，yk（ ）＝

当群X和群Y是同一个群时，RD（x，yk）就是传统意义上的Kakwani指数。根据公式（3）我们可以给出个体相对剥夺的一个简单的计算公式：

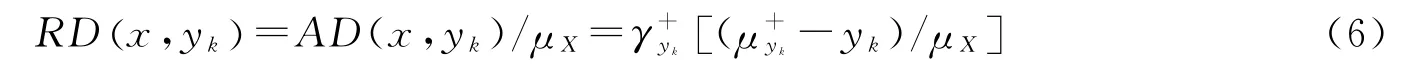
为了和传统的相对剥夺的概念相一致，群X对群Y中个体k的个体相对剥夺）也记为，这个记号的一个好处是我们可以认为群X的维数是可变的，RD具有如下性质：

性质1：在群X保持不变的条件下，RD（X，yk）是群Y中收入的严格递减函数，即如果yk＞yl，则RD（X，yk）＜RD（X，yl）。

性质2：RD（X，yk）取值范围在0和1之间，而且无量纲。

性质3：如果群Y中某个个体的收入比X中的最高收入都高，则群X对该个体的相对剥夺为0。

性质4：RD（X，yk）满足规模不变性，即如果群X中所有个体i的收入xi和群Y中个体k的收入yk都按同一比例变化，则RD（X，yk）不变。

性质5：群X中收入高于yk的两个个体间的收入转移，只要转移后两个个体的收入仍都高于yk，则RD（X，yk）不变；群X中收入低于yk的两个个体间的收入转移，只要转移后两个个体的收入仍都低于yk，则RD（X，yk）也不变。

但是个体绝对剥夺的很多重要性质，个体相对剥夺RD（X，yk）却不一定具备，如RD（X，yk）不一定是凹函数；它不仅与X中收入高于yk的个体有关，也与收入低于yk的个体有关，其中收入低于yk的个体对RD（X，yk）的影响主要是通过μX来实现的；此外个体相对剥夺不再满足平移不变公理和线性其次性公理等。但是，由于其取值在0和1之间、无量纲、规模不变性等性质，以及良好的图形表现工具，在实证分析中还是得到了广泛应用。

（二）群间个体相对剥夺曲线。Kakwani（1984）给出的个体相对剥夺测度只是我们群间个体相对剥夺的一个特殊情况（两个群相同），下面我们要对Kakwani（1984）的相对剥夺曲线绘制方法进行扩展，给出群内相对剥夺曲线和群间相对剥夺曲线的一个统一的分析框架。

设X，Y是两个收入群，群X的均值为μX，概率密度函数为dy为其概率分布函数；群Y的均值为μY，概率密度函数为为其概率分布函数，群Y中一个个体的收入为y0，根据Martín和Olmedo（2007）的结果，群X对群Y中收入为y0的个体的绝对剥夺可以写成：

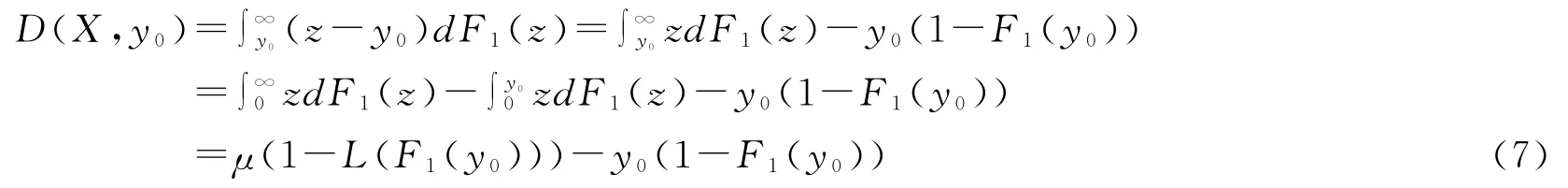
则群X对群Y中收入为y0的个体的相对剥夺即为：

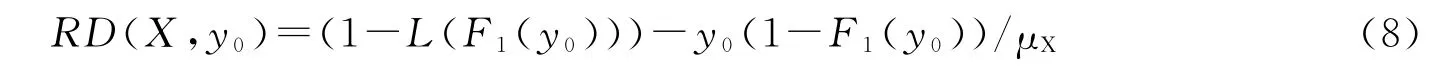
令p为分位数，则0＜p＜1，与p对应的群Y中个体收入为yp，则p＝F2（yp），那么，代入（8）式有：

我们称（9）式为群X对群Y中分位数p的相对剥夺，记为RD（X，p），这样给定群Y中的一个分位数p，我们就可以得到群X对p的相对剥夺RD（X，p），把这些点描绘在以分位数为横轴、以相对剥夺为纵轴的坐标平面上，就可以得到群X对群Y中个体的相对剥夺曲线。Kakwani给出的相对剥夺曲线是我们给出方法当群X和群Y是同一个群即F1＝F2＝F时的一个特例，所以（9）式就可写成：

RD（X，p）＝（1-L（p））-（F-1（p）／μX）（1-p），这里函数L（p）代表洛伦兹曲线，满足：（1）p＝0，L（p）＝0；（2）p＝1，L（p）＝1；（3）（dL（p）／dp）＝yp／μX；（4）（d2L（p）／dp2）＝1／f（yp）。所以

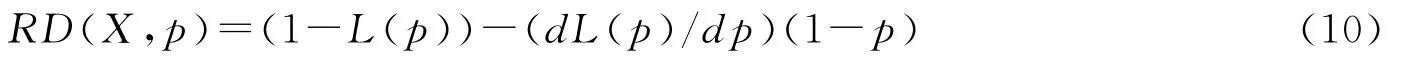
（10）式即为Kakwani（1984）给出的个体相对剥夺的计算公式，通过相对剥夺曲线，可以给出相对剥夺随分位数变化的一个直观认识。相对剥夺曲线具有以下特点：

（1）相对剥夺曲线是向右下方倾斜的一条曲线，但不是严格单调下降的，因为对应不同的分位数p，其对应的收入可能是相同的；

（2）当p＝0时，RD（X，p）不一定等于1，因为如果群Y中的最低收入不等于0，则群X对该收入的相对剥夺一定小于1；同样，当p＝1时，RD（X，p）也不一定等于0，因为群X中可能存在某些个体其收入比群Y的最高收入还要高。但是，如果X＝Y，则有p＝1，RD（X，p）＝0。

（3）相对剥夺曲线的陡峭程度取决于两个量：一是分位数p，二是概率密度函数f（x）。为简单起见我们以群X和群Y为同一群这一特殊情况加以证明，因为：RD（X，p）＝（1-L（p））-（dL（p）／dp）（1-p），所以dRD（X，p）／dp＝-（dL（p）／dp）-（d2L（p）／dp2）（1-p）＋（dL（p）／dp）＝-（d2L（p）／dp2）（1-p）＝-（1-p）／f（x）。

因此，如果p越小，f（x）越小，则dRD（X，p）／dp的绝对值越大，相对剥夺曲线越陡峭。

虽然，给了个体相对剥夺函数RD（X，p），我们就可以绘出相对剥夺曲线，但是实际绘制时往往不是采用RD（X，p），而是按下述步骤来进行：

（1）将群Y中所有个体按照收入递增的顺序排列；

（2）对群Y中的个体进行分组，找出每个分位数pi（可以是百分位或十分位），对应的个体的序号ki，然后根据序号找到其对应的收入yki；

四、群间总体剥夺及其性质

对群内所有个体的相对剥夺进行加权平均就得到一个群的总体相对剥夺，这个做法把一些不平等指数和个体相对剥夺建立起密切的联系，使得不平等指数有了其微观基础，对于加总的权重大多数文献采用的是等权重的方法，即如果一个全体有n个样本，则每个样本的权重就是1／n，例如Yitzhaki指数采用等权重进行加总得到绝对基尼系数，Kakwani指数采用等权重进行加总得到基尼系数，Imedio－Olmedo等（2011）定义了两个个体剥夺指数，并证明这两个个体剥夺指数采用等权重进行加总得到的总体剥夺分别为不平等指数绝对Bonferroni指数和绝对DeVergottini指数，而Cowell等（2004）则分析了个体相对剥夺的三种情况：BOP（和收入最高者相比）、AVE（和均值相比）和ATBO（和收入比他高的人相比），并采用不同的权重定义了加总后的不平等指数。根据上述研究文献采用等权重方法对Y中所有元素yk相对于群X受到的剥夺RD（X，yk）取算术平均，得到群X对群Y的相对剥夺：

定理3：（任国强，2011）RD（X，Y），RD（Y，X）均小于1。

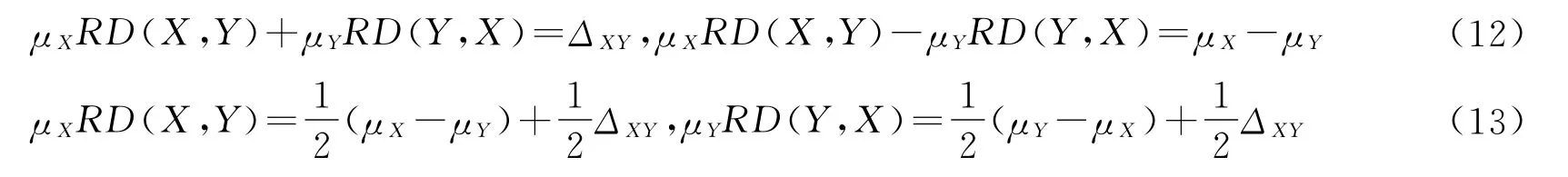
定理4：给了我们一个计算群X对群Y的相对剥夺RD（X，Y）和群Y对群X的相对剥夺RD（Y，X）的便捷方法，也即：

而且，当μX＝μY时，RD（X，Y）＝RD（Y，X）。

定理5：如果群X和群Y是分离的，即MinX（）＞MaxY（），则有RD（X，Y）＝1-（μY／μX），RD（Y，X）＝0。

证明：如果MinX（）＞MaxY（），则有μX-μY，所以RD（X，Y）＝1-（μY／μX），RD（Y，X）＝0。

定理6：RD（X，Y）＝RD（Y，X）的充分必要条件为μX＝μY；RD（X，Y）＞RD（Y，X）的充分必要条件为μX＞μY。

根据ΔXY的定义，有，该等式成立除非所有yj＝0，j＝1，2，…，m，所以，如果μX＝μY，则有RD（X，Y）＝RD（Y，X），反之，如果RD（X，Y）＝RD（Y，X），则有μX＝μY；如果μX＞μY，则有RD（X，Y）＞RD（Y，X），反之如果RD（X，Y）≥RD（Y，X），则有μX≥μY，RD（X，Y）＝RD（Y，X）的充分必要条件为μX＝μY；RD（X，Y）＞RD（Y，X）的充分必要条件为μX＞μY。

定理5、定理6表明，群间相对剥夺和两个群样本的均值有一定的关系，即如果两个群样本的均值相等，则这两个群的群间相对剥夺也相等，反过来也成立；如果一个群样本的均值大于另一个群样本的均值，则均值高的群对均值低的群的剥夺大于均值低的群对均值高的群的剥夺，反过来也成立。把群X和群Y的群间的收入差距分解为X对Y的相对剥夺RD（X，Y）和Y对X的相对剥夺RD（Y，X）两个指标，具有十分重要的现实意义。如果μX≥μY，则RD（X，Y）反映了两个群间的差异，而RD（Y，X）则反映了两个群间的交错情况；如果两个群是分离的，则RD（Y，X）＝0，假如有两个群Y1和Y2，它们的均值相等，即，根据群X与群群Y1和Y2的分离状况，群间相对剥夺的结果也是不一样的，假如群X与群Y1分离，群X与群Y2交错，则，而RD（Y1，X）＝0，RD（Y2，X）＞0，这一结果是采用均值比较来分析群间差距所不能得出的。

政府收入分配政策的一个重要目标是降低不同群体间的收入差距，特别是垄断行业和非垄断间的收入差距，那么哪些措施能够降低不同群间的收入差距呢？下面就进行具体的分析。

定理7：假设群X和群Y的均值分别为μX和μY，μX＞μY，则提高低收入群体Y中个体收入的任何措施，都会降低群X对群Y的相对剥夺。

除了提高低收入群体的收入可以达到降低群间的收入差距外，还有一种措施可以达到降低群间收入差距的目的，那就是改变低收入群体的收入分配状况。这一点虽然现在不能给出证明，但可以通过一个例子加以说明。

假设群X中有一个个体，收入为10 000，群Y中有两个个体收入分别为12 000和6 000，则μX＞μY，假如我们对群Y的收入分布做如下改变：高收入者收入降低1 000，低收入者收入增加1 000，这样得到的收入集合为Y0。显然，Y0的分配状况比Y要好，而且；但是，RD（X，Y）＝0.2，RD（X，Y0）＝0.15。这样就通过调节低收入者的收入分配状况，达到了降低群间收入差距的目的。这个结论也不是使用两个群的均值比作为度量群间收入差距的方法所能得出的。

定义3：如果RD（X，Y）≥RD（Y，X），则称群X对群Y相对剥夺占优，或群X相剥夺占优群Y，记为X≥RDY。

定理8：群间的相对剥夺关系是一个偏序关系。

说明：（1）当X＝Y时，RD（X，Y）＝RD（Y，X）＝GX＝GY，其中：GX和GY分别为群 X和群Y的基尼系数，所以群间的相对剥夺关系满足自反性；（2）当X≠Y时，如果群X对群Y相对剥夺占优，则有RD（X，Y）＞RD（Y，X），那么，群Y不对群X相对剥夺占优；所以，群间的相对剥夺关系满足反对称性；（3）如果群X对群Y相对剥夺占优，群Y对群Z相对剥夺占优，则有RD（X，Y）≥RD（Y，X），RD（Y，Z）≥RD（Z，Y），根据定理6可知μX≥μY，μY≥μZ，所以μX≥μZ，再根据定理6可知RD（X，Z）≥RD（Z，X）；所以，群间的相对剥夺关系满足传递性。一个关系如果满足自反性、反对称性和传递性，则该关系就是偏序关系。所以群间的相对剥夺关系是偏序关系。

定理9：群间的相对剥夺RD（X，Y）满足线性齐次性。

证明：假设λ＞0，由于当群X和群Y中每个个体的收入都变为原来的λ倍时，则其均值也变为原来的λ倍，且

定理10：群间相对剥夺RD（X，Y）满足加和可分解性。即对所有的X1，X2⊆X，使得并且，那么

证明：根据群X对群Y中个体k的加和可分性可得，所以

定理11：群间的相对剥夺RD（X，Y）满足焦点性公理，即RD（X，Y）与X中收入比Y中最低收入还低的个体无关，也与Y中收入比X中最高收入还高的个体无关，也即RD（X，Y）＝RD（X-MinX（Y），Y-MaxY（X））

证明：当i∈MinX（Y），∀yk∈Y，都有ADXY（xi，yk）＝0，所以RD（X，Y）与X中收入比Y中最低收入还低的个体无关；当k∈MaxY（X）时，∀xi∈X，都有ADXY（xi，yk）＝0，所以RD（X，Y）与Y中收入比X中最高收入还高的个体无关。

五、实证分析

（一）数据。本文所用数据来自CGSS2008全国调查数据，该调查样本包含27个省市的6 000个个体，其中城镇数据3 982个，农村数据2 118个。剔除样本中年职业收入、职业外收入指标值为不知道、拒绝回答和不适用的个体，最终剩余符合要求的城镇数据2 980个、农村数据1 690个。本文中将区域指标为城镇的所有样本个体集合设为群U，将区域指标为农村的所有样本个体集合设为群R。将两个群中分别按年人均收入的递增顺序对群内个体进行排列。城镇群体和农村群体的十分位数、十分位数对应个体序号及该个体收入见表1。

表1 城镇群体和农村群体的十分位数据特征

（二）城镇和农村内部的个体相对剥夺。对于每个分位数，我们采用第三部分给出的方法，分别计算与该分位数对应的农村个体被农村群体的相对剥夺和城镇个体被城镇群体的相对剥夺，结果见表2。

表2 对应城镇群体和农村群体十分位数据的相对剥夺

根据表2中数据可以得到城镇和农村内部的个体相对剥夺曲线，见图1和图2。

图1 城镇内部的个体相对剥夺曲线

图2 农村内部的个体相对剥夺曲线

从表2和图1、图2可知，城镇居民对应各分位数的相对剥夺，从pi＝0到pi＝0.1、从pi＝0.1到pi＝0.2变动幅度很大，均超过了0.1；从pi＝0.9到pi＝1变动的幅度也很大，其值超过0.15，其原因主要是收入变化幅度较大，而其他各阶段变化的幅度都比较小。另一方面，城镇内部的个体相对剥夺曲线上的点大部分落在（0，1）和（1，0）点连线的下方，由于相对剥夺曲线和两个坐标轴围成的面积为基尼系数，说明城镇内部差距的基尼系数小于0.5；但是农村内部的个体剥夺呈现出和城镇居民明显不同的特点，从pi＝0到pi＝0.1以及从pi＝0.6以后的变动幅度都超过了0.1，而且农村内部的个体相对剥夺曲线上的点大部分落在（0，1）和（1，0）点连线的上方，说明农村内部差距的基尼系数大于0.5；从城镇内部和农村内部每一分位数点相对剥夺的数值来看，除个别点外，农村内部的个体相对剥夺要高于城镇内部。

（三）城镇群体对农村个体和农村群体对城市个体的相对剥夺。对于每个分位数，我们采用第三部分给出的方法，分别计算与该分位数对应的农村个体被城镇群体的相对剥夺和城镇个体被农村群体的相对剥夺，结果见表3。

表3 对于每一分位数城镇群体对农村个体和农村群体对城镇个体的相对剥夺

根据表3数据可以得到城镇群体对农村个体的相对剥夺曲线和农村群体对城镇个体的相对剥夺曲线，见图3和图4。

图3 城镇群体对农村个体的相对剥夺曲线

图4 农村群体对城镇个体的相对剥夺曲线

由表3和图3、图4可知，对于每一分位数，城镇群体对农村个体的相对剥夺远远高于农村群体对城镇个体的相对剥夺，其原因在于对每一分位数城镇居民收入比重比该分位数对应的农村居民收入比重都要高；农村对城镇最低收入的个体的相对剥夺很高，达到了0.9766，说明城镇中最低收入也很低，大部分农村居民的收入都高于他，但是对其他每一分位数，农村群体对城镇个体的相对剥夺基本上都大于0（除了pi＝1外），但是数值比较小，说明每一分位数上农村居民中收入高于城镇居民收入的比重比较低。

（四）城镇与农村群体的群间剥夺和群内剥夺。利用定理4的推论（14）式和（15）式，我们很容易计算任意两个群间的相对剥夺，采用这两个公式可以计算出城镇和农村群体内部的相对剥夺、城镇对农村的群间相对剥夺以及农村对城镇的群间相对剥夺，见表4。

表4 不同群体间的相对剥夺

从表4可知，农村居民内部收入差距较大，基尼系数达到了0.542689，城镇居民内部收入差距略小于农村居民，基尼系数为0.452422。城镇对农村的相对剥夺达到了0.748796，处于一个较高的水平，然而农村居民对城镇居民的相对剥夺则较小，仅为0.223951，而且城镇居民对农村居民的相对剥夺远远高于农村居民对城镇居民的相对剥夺，说明城镇居民的总体收入水平远远高于农村居民，农村居民的收入水平要赶上城镇居民还有一个很长的路要走。

六、结论及未来展望

本文在已有研究的基础上，对不同群间的个体进行比较，分别研究了群间个体绝对剥夺、群间个体相对剥夺、不同群间总剥夺测度的性质、公理化特征及其具体形式，并将相对剥夺曲线扩展到不同群之间，给出了一个群相对于另一个群的相对剥夺曲线的绘制方法。与以往研究成果相比，本文在以下方面取得一定进展：第一，将参照群的思想集成到群间剥夺的测度模型中，形成了统一的分析框架，得到了一个群对另一个群中个体的绝对剥夺测度公式，并证明一个个体剥夺函数如果满足聚焦性公理、平移不变性公理、线性齐次性公理、加和可分性公理及正规化公理，则该函数就是我们给出的个体绝对剥夺函数，在上述框架下群内个体绝对剥夺只是个体所在群和参照群相同时的一个特例；第二，在群间个体绝对剥夺的基础上给出了群间个体相对剥夺的测度公式并分析了其性质，以此为基础，将Kakwani的相对剥夺曲线理论扩展到不同群之间，绘制出群间相对剥夺曲线；第三，给出一个群对另一个群相对剥夺的计算公式（此时群内不平等指标——基尼系数只是两个群相等时群间相对剥夺的一个特例），并对群间相对剥夺的性质进行了详细的探讨，该研究使我们对群间的收入差距有了更进一步的认识，与平均收入比这一指标相比，两个群体之间的相对剥夺更能反映群间的收入差距，平均收入高的群体对平均收入低的群体的相对剥夺反映了高收入群体和低收入群体间的收入差异状况，而平均收入低的群体对平均收入高的群体的相对剥夺则反映了两个群间的收入交错状况，后者更为重要，在一定程度上代表了低收入群体的希望，也是调节群间收入差距应重点关注之所在，任何提高低收入群体中个体收入的措施，都会降低高收入群体和低收入群体的群间收入差距；第四，利用CGSS2008全国调查数据，绘制了城镇内部、农村内部、城镇对农村和农村对城镇的相对剥夺曲线，并计算了它们总体的相对剥夺，对理论成果进行了实证检验。

尽管研究得到了一些进展，但仍有一些问题需要进一步研究，特别是群间个体绝对剥夺除以参照群的收入均值得到群间个体相对剥夺的做法缺乏强有力的理论支撑，但却是目前最好的处理方法，其特例Kakwani指数由于不满足平移不变性和焦点性公理也得到了很多学者的批评。因此，如何得到一个具有“更好”的个体相对剥夺测度成为未来有待解决的一个重要课题。

［1］洪兴建.一个新的基尼系数子群分解公式——兼论中国总体基尼系数的城乡分解［J］.经济学季刊，2009，（1）：307-324.

［2］任国强，尚金艳.基于相对剥夺理论的基尼系数子群分解方法研究［J］.数量经济技术经济研究，2011，（8）：103-114.

［3］Berrebi Z M，Silber J.Income inequality indices and deprivation：A generalization［J］.Quarterly Journal of Economics，1985，100（3）：807-810.

［4］Bossert W，D’Ambrosio C.Reference groups and individual deprivation［J］.Economics Letters，2006，90（3）：421-426.

［5］Bylsma W H，Major B.Social comparisons and contentment：Exploring the psychological costs of the gender wage gap［J］.Psychology of Women Quarterly，1994，18（2）：241-250.

［6］Chakravarty S R，Chakraborty A B.On indices of relative deprivation［J］.Economics Letters，1984，14（2／3）：283-287.

［7］Chakravarty S R，Mukherjee D.Measures of deprivation and their meaning in terms of social satisfaction［J］，Theory and Decision，1999，47（1）：89-100.

［8］Ebert U，Moyes P.An axiomatic characterization of Yitzhaki’s index of individual deprivation［J］.Economics Letters，2000，68（3）：263-270.

［9］Eibner C E，Evans W N.Relative deprivation，poor health habits and mortality［J］.The Journal of Human Resources，2005，40（3）：591-620.

［10］Esposito L.Upper boundedness for the measurement of relative deprivation［J］.Review of Income and Wealth，2010，56（3）：632-639.

［11］Ferrer－i-Carbonell A.Income and well-being：An empirical analysis of the comparison income effect［J］.Journal of Public Economics，2005，89（5-6）：997-1019.

［12］Frank R H.Falling behind：How rising inequality harms the middle class［M］.Berkeley：University of California Press，2007.

［13］Cowell F A，Ebert U.Complaints and inequality［J］.Social Choice and Welfare，23（1）：71-89.

［14］Heather J S，Thomas F P，Gina M P，et al.Relative deprivation：A theoretical and meta-analytic review［J］.Personality and Social Psychology Review，2011，16（3）：203-232.

［15］Kakwani N.The relative deprivation curve and its applications［J］.Journal of Business and Economic Statistics，1984，2（4）：384-394.

［16］Lhila A，Simon K I.Relative deprivation and child health in the USA［J］.Social Science and Medicine，2010，71（4）：777-785.

［17］Imedio－Olmedo L J，Parrado-Gallardo E M，Bárcena-Martin E.Income inequality indices interpreted as measures of relative deprivation／Satisfaction［J］.Social Indicators Research，2012，109（3）：471-491.

［18］Bárcena-Matin E，Imedio-Olmedo L，Martin-Reyes G.Inequality and deprivation within and between groups：An illustration of European Union countries［J］.Journal of Economic Inequality，2007，5（3）：323-337.

［19］Podder N.Relative deprivation，envy and economic inequality［J］.Kyklos，1996，49（3）：353-376.

［20］Paul S.An index of relative deprivation［J］.Economics letters，1991，36（3）：337-341.

［21］Runciman W G.Relative deprivation and social justice：A study of attitudes to social inequality in twentieth-century England［M］.Berkeley：University of California Press，1966.

［22］Silber J，Verme P.Distributional change，reference groups and the measurement of relative deprivation［J］.Research on Economic Inequality，2010，18（1）：197-217.

［23］Silber J，Verme P.Relative deprivation，reference groups and the assessment of standard of living［J］，Economic Systems，2012，36（1）：31-45.

［24］Stouffer S A，Suchman E A ，De Vinney L C，Star S A，Williams R M.The American soldier：Adjustment during army life［M］.Princeton，NJ：Princeton University Press，1949.

［25］Yitzhaki S.Relative deprivation and the Gini coefficient［J］.The Quarterly Journal of Economics，1979，93（2）：321-324.