基于GeoStudio 软件的边坡稳定分析

徐凯 王赟 周桂云 顾荣蓉

(金陵科技学院建筑工程学院，江苏南京 211169)

1 概述

随着世界上各个国家大规模工程建设的开展，开始出现了各种边坡灾害，造成了很大的损失，例如泥石流威胁城市安全、滑坡导致交通中断、城镇被掩埋、公路中断等，这些危害使得人们把边坡的稳定性研究作为一项课题来分析［1］。边坡稳定分析方法主要有刚体极限平衡法、数值分析方法、极限分析法、滑移线场法等。极限平衡法主要以摩尔—库仑准则作为基础，通过给出假想的简单破坏面，并将滑动面以上的滑体分成若干垂直条块，建立静力平衡方程，辅以一定假设条件计算得出结果，刚体极限平衡法是目前岩土工程界最为广泛采用的方法，原因在于其原理简单、计算方便、且能给出易于接受的稳定性指标［2］。本文运用GeoStudio软件，以一简单粘性土坡为例，分别采用3种简化方法搜索滑动面、计算稳定安全系数并对各条块进行受力分析，并比较各种方法对安全系数的影响。

2 刚体极限平衡法基本理论

2.1 基本原理［1］

1)安全系数的定义。

安全系数F的定义是将土的抗剪强度指标降低为c'/F和tanφ'/F，则土坡沿着某一滑裂面滑动时达到极限平衡状态，即:

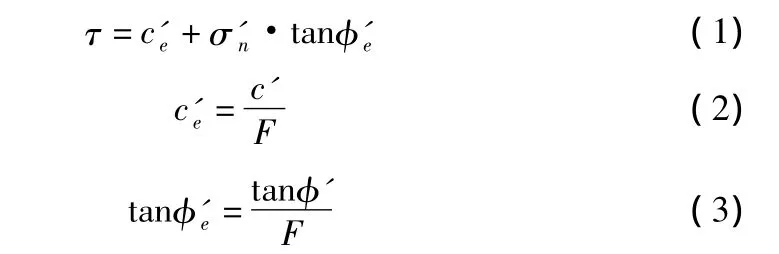
将强度指标储备作为安全系数定义的方法是经过多年的实践证明，已被工程界广泛承认的一种方法，但在进行数值计算时会存在迭代、收敛等方面的问题。

2)摩尔—库仑强度准则。

假设土体的一部分沿着某一滑裂面滑动，在此滑裂面上，土体处处达到极限平衡，即正应力σ'n和剪应力τ满足摩尔—库仑强度准则。设土条底部的法向力和切向力分别为N和T，则有:

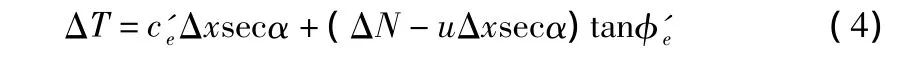
其中，α为土条底倾角，tanα=dy/dx;u为孔隙水压力，孔隙水压力系数定义为:

3)静力平衡条件。

把滑动土体垂直分成若干土条，每个土条和整个滑动土体都同时满足力和力矩平衡条件。在静力平衡方程组中，未知量的个数超过了方程式的个数，采用对多余未知数作假定来解决这一超静定问题，使未知数的个数等于方程个数，求解安全系数的值。

2.2 静力平衡方程［3］

对于如图1所示的条块i，考虑垂直方向力的平衡。

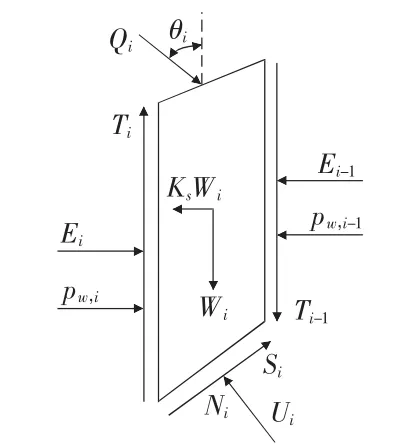
图1 条块体的受力分析

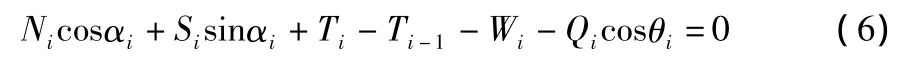
类似地，考虑水平方向力的平衡:

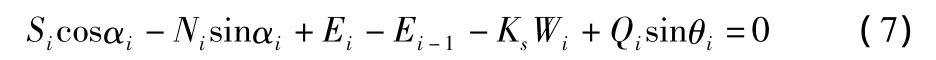
进一步考虑作用在条块i上的力对同一点(x0，y0)(即滑动体的假想或实际转动中心)的力矩平衡，将会得到下面的关系:

其中，滑动体的可能滑动方向自右上向左上时，在出现两个计算符号处，取上面一个计算符号;滑动体的可能滑动方向自左上向右下时，在出现两个计算符号处，取下面一个计算符号;Xni=xni－ x0，Yni=y0－ yni，Xpi=xpi－ x0，Ypi=y0－ ypi，Xp，i－1=xp，i－1－ x0，Yp，i－1=y0－ yp，i－1，Xci=xci－ x0，Yci=y0－ yci，Xqi=xqi－ x0，Yqi=y0－yqi。对滑动面为圆弧滑动体时，其圆心就是真正的求矩中心，土条底部法向力Ni是通过圆心的，无论土条底部法向力Ni的作用点位于土条底部哪一点，它对圆心的力矩均为零。而土条底部剪切力Si对圆心的力臂就是圆弧的半径R。则式(8)可简化为:

处于极限平衡状态时，作用在滑动土体上的所有的力应满足整体力和力矩的平衡。同一界面上的条间力是一对作用力和反作用力，分析整体的力和力矩平衡时，它们将相互抵消，因此，它们整体的力和力矩平衡方程中不会出现。根据式(6)，可得:

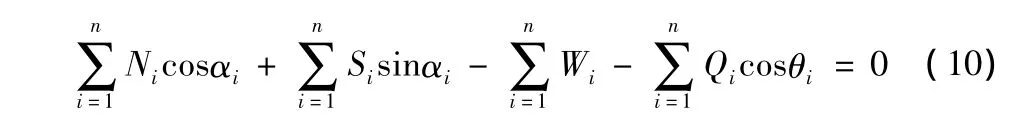
类似地，根据式(7)，可得:

根据式(8)，可得:

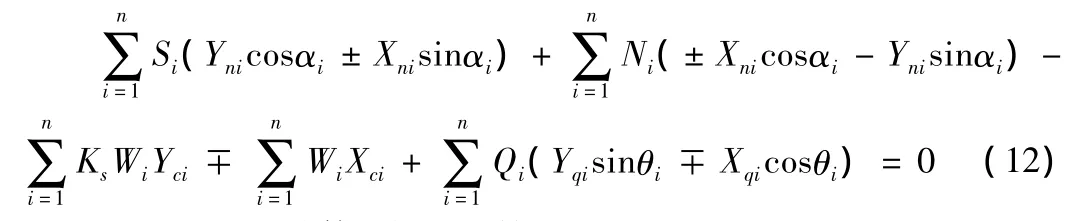
对于圆弧滑动体，式(12)简化为:

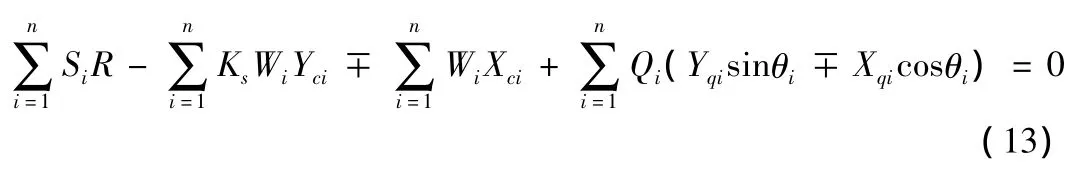
其中，式(10)和式(11)分别为垂直方向及水平方向整体力的平衡方程;式(12)和式(13)为整体力矩平衡方程。

3 算例分析

1)计算模型。图2为一简单粘性土坡，高25 m，坡比1∶2，碾压土的容重 γ=20 kN/m3，内摩擦角 φ =26.6°，粘聚力c=10 kPa。现对如图2所示的圆弧滑动面用常用极限平衡条分法进行安全系数的计算。

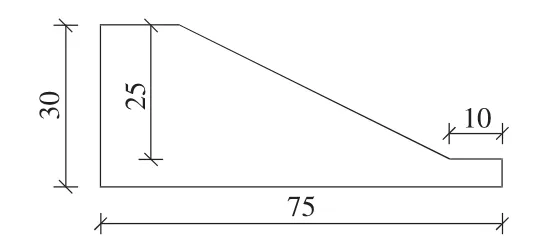
图2 算例边坡模型图（单位：m）

2)计算成果。运用GeoStudio软件对图2的边坡进行稳定分析，分别用瑞典法、Bishop法、Morgenstern-Price法和Spencer法进行计算，各种方法计算的安全系数、临界滑裂面如图3～图6所示。

图3 瑞典法安全系数和临界滑裂面

瑞典法的安全系数是1.345，Bishop法的安全系数是1.379，Spencer法的安全系数是1.378，Morgenstern-Price法的安全系数是1.378;由瑞典法计算得到的安全系数最小，Bishop法的安全系数最大，Bishop法、Spencer法和Morgenstern-Price法计算出的安全系数相当接近，且Spencer法以及Morgenstern-Price法计算所得的安全系数相同;由此可以得出这样的结论:由于不考虑条间力的作用，严格地说，不满足条块力和力矩平衡条件，仅能满足可能滑动体的整体力矩平衡条件，用瑞典法得到的数值有较大的误差，而Spencer法和Morgenstern-Price法这两种严格条分法计算得到的数值相对准确。

图4 Bishop法最小安全系数和临界滑裂面

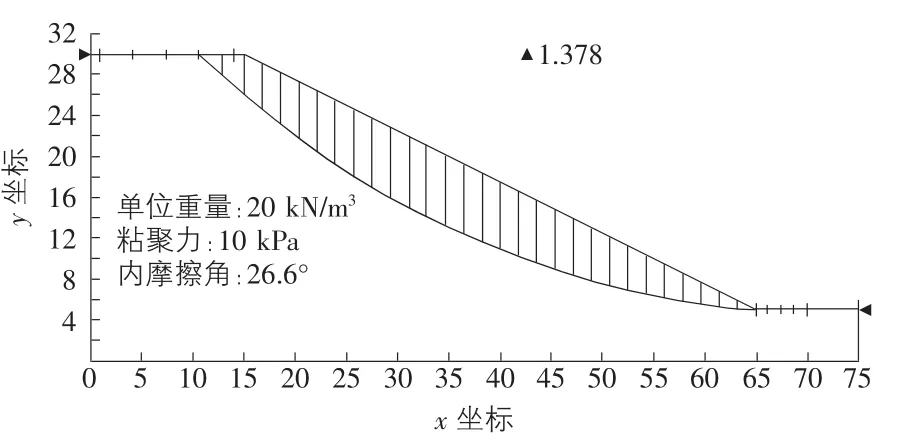
图5 Spencer安全系数和临界滑裂面

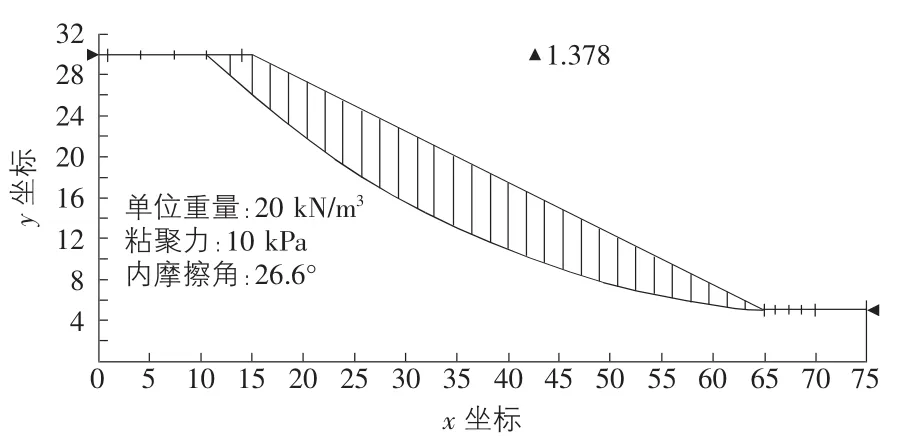
图6 Morgenstern-Price法安全系数和临界滑裂面

4 结语

本文论述了极限平衡法的基本原理，运用GeoStudio软件分别用瑞典法、Bishop法、Morgenstern-Price法和Spencer法对算例进行计算分析比较。计算结果表明:非严格条分法由于不能严格满足条块力和力矩平衡条件，仅仅满足滑动体的整体力矩平衡条件，计算得到的安全系数有较大的误差;而严格条分法计算得到的安全系数相对准确。

［1］陈祖煜.土质边坡的稳定分析——原理.方法.程序［M］.北京:中国水利水电出版社，2003.

［2］汪承亮.极限分析法在边坡稳定分析及挡土墙土压力计算中的应用［D］.合肥:合肥工业大学，2010.

［3］郑颖人.边坡与滑坡工程治理［M］.北京:人民交通出版社，2010.