在水平成层土体中波动数值模拟的人工边界★

崔高航 王兆亮 刘守花

(东北林业大学土木工程学院，黑龙江哈尔滨 150040)

0 引言

人工边界条件又称为透射或吸收边界条件，理论上对连续介质的模拟更加的精确;目的是保证能量在通过人工边界的时候，能与连续介质一样能够完全的透射或者吸收，而不会由于人工边界的设置而发生反射。

ABAQUS［1］作为通用的有限元软件，分析计算功能和模拟性能在国际上处于领先的地位，它的分析过程、单元模型和材料模型等的种类比较齐全。ABAQUS在分析弹性问题或者非线性的组合问题的时候，获得的分析结果相对于其他的有限元软件都是比较准确的。本文基于ABAQUS软件平台和透射边界理论，利用Microsoft Visual Studio 2008平台的 Intel(R)Fortran Compiler 11.0.061编写位移迭代程序与ABAQUS软件的DISP边界条件子程序接口链接，实现透射边界条件的施加;同时，基于ABAQUS软件中动力无限元理论，利用四节点无限单元引入阻尼(阻尼矩阵)给出无限元边界模型;最后，考虑足够远的尺寸，建立符合进度要求远置边界模型，并将其分析结果参考为精确解用于对比分析;最后建立相同尺寸的固定边界模型。算例分析，验证了本文在成层土体中施加透射边界方法的合理性和有效性。此外，通过与其他边界模型数据结果对比分析，结果表明，通过本文方法所施加的透射边界在处理环境振动问题中的精度要优于其他边界条件。

1 透射边界

1.1 透射边界定义

透射边界是通过给出单向波动的一般表达式和人工视波速ca(通常取剪切波速，即ca=cs)，建立了透射理论和相应的多次透射公式［2］(MTF)(如图1所示)。理论依据是单侧行波解的一般表达式，通过对波在穿越边界的过程分析，获得可行的位移边界条件(方式:内节点位移代替边界节点位移)。透射边界概念与理论是我国学者廖振鹏等于20世纪80年代初提出的，具有物理概念明确、透射效果好、计算简单，且很容易和有限元等数值解法相结合等优点，近年来得到广泛的应用。

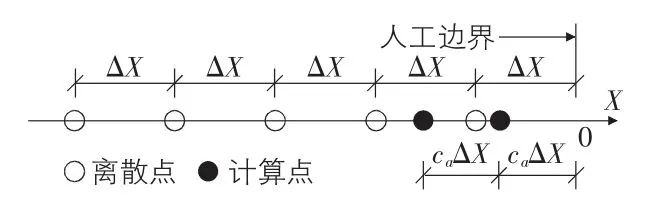
图1 多次透射（MTF）公式的几何关系

N阶多次透射公式(MTF)为:

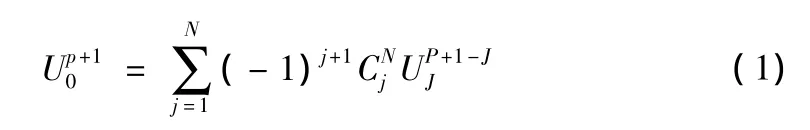
1.2 透射边界的稳定性

任何人工边界都存在着稳定性问题。透射边界的稳定性问题也是保证近场波动数值模拟精度的关键问题。其中，高频振荡和低频飘移是透射边界模型精度主要的数值失稳现象。

参考相关文献采取处理措施如下:

1)消除高频振荡失稳的措施。

［3］～［5］在有限元计算中增加与应变速度相关的阻尼，通常采用瑞利阻尼(C=αM+βK)形式。而通用有限元软件ABAQUS具有瑞利阻尼模式，在建立分析模型时，可按属性参数直接设置。并要求在保证数值积分稳定的情况下，β值尽量取的小一些。研究表明:施加相关阻尼的措施，可以较好的限制高频振荡失稳，而且对低频波动影响可以降低到一定的范围，从而获得较好的数值稳定性。

2)消除零频飘移失稳的措施。

参考文献［5］～［7］认为透射边界数值计算中的零频和零波数分量进入计算区，是导致人工边界飘移失稳的原因。在MTF计算中，通过引入一个远小于1的正数算子γ对多次透射公式(式(1))进行修正。修正后的多次透射公式为:

该算子一般取γ≤0.05的正数，但不宜过小，主要结合经验和试算确定。从实用的观点来看，MTF具有普适性、可控性、时空解耦性，在保证模拟精度的情况下，能够在计算机上稳定实现。

1.3 透射边界的模型实现

一般情况下，MTF的计算点x=－jcaΔt与离散节点x=－nΔx不一致，故需通过线性内插方法获得计算点位移。MTF的数值实现方法有两种:空间内插和时间内插。本文采用第一种空间插值形式(见图1)。

在工程应用中，MTF一般采取一阶、二阶透射公式。经过实践证明，MTF的精度是可控的，二阶透射公式已经具有较高的工程可用精度。故本文在下面的算例中采用空间三点两插值形式，取人工边界区前n(透射公式阶数:n=2)时刻的位移计算人工边界点位移。

图2 二维土体模型人工边界计算区

参考图2，二阶透射公式如下:

经过插值后的二阶透射公式变为:

本文通过考虑波源问题进行建模(见图3)，外行波场不通过波场分离获得，全波场［2］即为穿越人工边界的外行波场，MTF可直接由全位移表出。透射边界在ABAQUS中的实现步骤如下:

1)划分离散网格，获得具有时步积分格式的内节点运动方程。要求空间步距为Δx，且应满足在有意义的波长内含有Δx的数量不应少于6个～8个，时间步距Δt应满足稳定条件即Δt≤Δx/cmax，cmax为单元的最大波速值［2］。

2)利用动力响应分析中的有限差分法［8］，获得内节点运动方程:

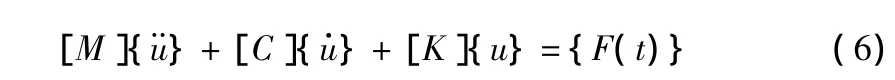
并对式(6)求解。其中，利用MATLAB数学软件获得单元的刚度矩阵K;单元质量矩阵M由集中质量模型通过MATLAB编程获得;F(t)通过集中力的等效荷载列阵获得。利用ABAQUS软件对土体模型进行模态分析，提取模型前2阶固有频率f1，f2，选取合适的阻尼比ε，进而确定α，β参数，最终获得瑞利阻尼矩阵C=αM+ βK。

3)在计算区域内选取计算点和离散点，通过空间内插方法，并且用计算点数据来表示边界节点的运动方程，MTF由该运动方程表示。

4)基于ABAQUS软件平台的DISP［9］子程序接口，通过FORTRAN语言来编写位移迭代的程序，编写的程序代码如下:

SUBROUTINE DISP(U，KSTEP，KINC，MODE，NOEL，JDOF，COORDS)

INCLUDE‘TOUSHE_BIANJIE.INC’

DIMENSION U，TIME，COORDS

定义位移边界条件U(根据边界逐个节点位移时程编辑迭代程序)

RETURN

END

程序运行合格后，通过Job模块General选项卡中的User subroutine file路径，完成模型透射边界条件的施加。

2 无限元边界

2.1 无限元

早在1977年的时候，无限元的概念已经被Zienkiewicz提出，无限元在几何上是无限大的但是由有限个单元组成的［10］。无限元法在解决半无限和无限域等空间问题时经常与有限元方法联合使用，常被看作是对有限元法进一步的补充，故有“半有限元”的称号。本文在ABAQUS有限元软件的荷载分析步模块，建立随时间变化的脉冲荷载，荷载作用点的位置按模型尺寸考虑。由于涉及动力分析问题，故采用动力分析中的无限元建立无限元模型并进行分析(见图4)，要求模拟单元采用四节点无限单元(见图5)，并且确保节点应按逆时针的规则进行编号和单元的第一个面应为有限元和无限元的交接面［11］。

图3 透射边界模型示意图

图4 无限元模型示意图

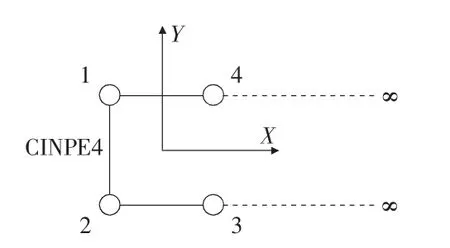
图5 四节点无限单元

2.2 无限元的原理

边界面反射并引起分析网格能量叠加，这是波在传播过程中通过人工截断边界时，所面临的最大问题。在ABAQUS动力分析中，无限元对这种波的传播问题有比较好的处理方法。通过对线性土体中一维波的传导进行分析，获得波传导的动力平衡方程为:

其中，ρ为密度;E为弹性模量;x为轴向坐标。

则当波传导到边界截面上时，波的形式为:

反射波的形式为:

为了达到不出现反射的情况，可以在边界上设置一个阻尼边界条件，使波动能量能通过边界，向无穷远处传播。

边界上的应力:

在边界上设定一个阻尼边界条件:

为了消除反射波的影响，假定不存在反射波，并联立式(9)和式(10)则可得到:

也就是说，只要边界阻尼参数选择合适，就可模拟无反射的情况。ABAQUS软件在动力分析无限元中考虑了阻尼的设置，从而可以保证波在通过截断边界时，波动能量被无限域吸收，从而对分析区域的影响可控制在允许范围之内。

3 算例分析

3.1 参数设置

本文将成层土体分两层，上层厚度5 m，下层厚度15 m。通过ABAQUS通用有限元软件建立远置边界模型，同时将计算结果作为精确解用于对比，模型尺寸取1 000 m×200 m，单元尺寸取Δx=Δy=1 m;其他边界模型尺寸取60 m×20 m，单元尺寸取Δx=Δy=1 m;其中，无限元边界取 Δx=30 m，Δy=1 m。荷载为作用于模型顶面中心(即(0，20)或(0，200))沿负Y方向的脉冲荷载，最大值Fmax=1.5×104N，荷载幅值曲线如下(见图6)。

图6 脉冲荷载幅值曲线

其中，分析步采用ABAQUS/Explicit动力显式分析步，计算分析步总长度step=6 s。表1列出所需要的模型参数。

表1 材料参数表

3.2 结果分析

在地面，取距震源5 m点处;在地下，取距震源深度为3 m，5 m和10 m点处，作为观察点提取Y方向的位移。图7～图10给出了在不同观察点处采用不同边界条件的位移反应时程曲线。

图7 地表距震源5 m点计算结果对比图

图8 地下距震源3 m点计算结果对比图

图9 地下距震源5 m点计算结果对比图

1)从图7～图10可以看出，垂向3 m，5 m和10 m点处的位移幅值，随着与震源距离的增大，出现明显的衰减趋势;分析图7和图9，地面5 m点处振动幅值要小于地下5 m点的振动幅值，说明振动在传播过程中，在不同方向与震源相同距离处，振动衰减程度是不同的。对比图7和图9中，波动能量在水平方向的衰减幅度要高于竖向，这与波在土中的传播规律相吻合。

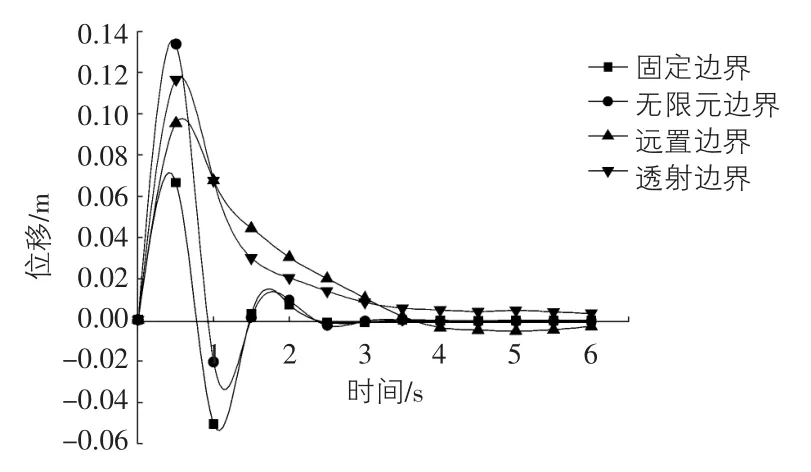
图10 地下距震源10 m点计算结果对比图

2)由图7～图10中的固定边界模型计算数据曲线，可以发现:在前1 s时间段内，波动主要由入射波引起的，在1 s～2 s左右时间段内，波动主要由反射波引起的。说明:振动在传播到固定边界时，波动能量不能透过边界，而在半无限土体中形成反射现象，这与设置边界条件的初衷不符。

3)采用无限元边界时，由于模型设置了阻尼矩阵，相当于添加了吸收边界条件。虽然反射现象依然存在，但相对固定边界，反射幅值已经明显减弱。

4)通过透射边界模型结果与远置边界的模型计算结果(精确解)进行比较，可以发现:透射边界结果与精确解更接近，能够较好的模拟振动波在半无限土体中的传播。说明，在成层土体中施加透射边界的方法，可以获得与精确解总体趋势符合程度较好的效果。因此，本文施加透射边界的方法是可行并且有效的。

5)通过对地下5 m点与3 m，10 m点位移时程比较，说明本文基于ABAQUS软件在不同介质分界面处施加透射位移边界条件也是同样适用的。

4 结语

人工边界的选取将很大程度上决定数值模型的精度。基于此，本文在对成层土体建立分析模型时，考虑透射边界理论和ABAQUS软件平台及子程序接口，提出了在成层土体中施加透射边界方法。该方法通过算例分析，表明是合理的;通过与无限元边界、固定边界、远置边界的模型结果比较，表明精度是可靠的;并且具有较高的实用价值，通过编程可以扩展复杂的二维问题和三维问题。

参考文献:

［1］庄 茁.ABAQUS非线性有限元分析与实例［M］.北京:科学出版社，2005:1-21.

［2］廖振鹏.工程波动导论［M］.第2版.北京:科学出版社，2002:232-285.

［3］廖振鹏，周正华，张艳红.波动数值模拟中透射边界的稳定实现［J］.地球物理学报，2002，45(4):533-545.

［4］李小军，廖振鹏.非线性结构动力方程求解的显示差分格式的特性分析［J］.工程力学，1993，10(3):143-148.

［5］李小军，杨 宇.透射边界稳定性控制措施探讨［J］.岩土工程学报，2012，34(4):641-645.

［6］周正华，廖振鹏.消除多次透射公式飘移失稳的措施［J］.力学学报，2001，33(4):550-554.

［7］杨 宇.场地地震波动中透射边界稳定性问题研究［D］.北京:中国地震局地球物理研究所，2011.

［8］周昌玉，贺小华.有限元分析的基本方法及工程应用［M］.北京:化学工业出版社，2006:46-76.

［9］李 帆，巴振宁，肖成志，等.波动数值模拟中人工透射边界的实现技术［J］.自然灾害学报，2010，19(4):49-53.

［10］Zienkiewicz O C.Diffraction and refraction of surface waves using finite and infinite elements［J］.International Journal for Numerical Methods in Engineering，1977(11):1270-1293.

［11］费 康，张建伟.ABAQUS在岩土工程中的应用［M］.北京:中国水利水电出版社，2010:44-88.