岩石中爆炸成坑的DDA模拟

2014-11-09孙淑美范一锴

山西建筑 2014年7期

孙淑美陈洁范一锴

(1.国家知识产权局专利局专利审查协作北京中心材料工程发明审查部，北京 100190;2.中国林业科学研究院，北京 100091;3.空军第一建筑安装工程总队，北京 100076)

物理试验是研究爆炸冲击问题的重要手段，但由于爆炸荷载的特殊性，物理试验有着固有的局限。随着计算机技术和数学科学的发展，数值模拟能力越来越强大，逐渐成为一个与物理试验互补的最佳研究手段。在物理试验的边界条件及提供的关键参数基础上，基于数学的推导和计算机大规模运算，可以模拟整个物理试验的过程，获取研究者所关注的技术指标［1］。

非连续变形分析(DDA，Discontinuous Deformation Analysis)是近年来在非连续大变形分析领域的后起之秀，对于爆破这种伴随大变形、开裂、材料块体的分离运动效应的物理过程的模拟，具有独特的优势［2］。赵根、刘红岩、朱传云等［3-5］对 DDA 应用于爆破领域进行探讨，证实其可行性，但在模拟过程中，爆炸荷载的取值和添加都采用经验估计方法，本研究拟对非连续变形分析在爆破成坑过程的模拟上做出一些改进，即在建模和参数设置时考虑了岩体中爆炸破坏特性以及炸药的状态方程，规范其爆炸荷载的取值和添加方法，使之能更好地应用于爆破分析。

1 总体流程

DDA方法已具备块体系统动力学分析的能力，但是用于爆炸荷载效应的计算，还需要考虑爆炸荷载的相关细节，简言之就是爆炸荷载的计算和加载问题。炸药引爆后除了刚开始的电磁、热辐射、冲击波，作用于介质时间最长的还是爆炸后生成的气体。本模拟中所需要的爆炸荷载即爆轰产物(气体)的压力p，这一参数可以通过炸药的状态方程求出。状态方程是用来描述爆轰产物的p—V—T关系，可以精确地反映爆轰产物的膨胀驱动做功过程。在围岩中爆破时，爆炸近区发生急剧的变化，包括压缩波的传播、塑性变形的发生、介质运动的破坏以及爆炸空腔的形成。从炮孔向外依次可分为汽化区、液化区、破碎区、裂纹区和弹性区。炮孔和裂纹区之间的区域变化过程十分复杂，要对这部分进行模拟耗费巨大，目前DDA方法也不能胜任这一工作，但本研究重点是弹坑形成过程分析，关注这一区域也没有必要，因此，可进行合理的简化。在模拟中，不考虑裂纹区以内的区域，参考相关文献，在炮孔周围预设一定大小的“空腔区”，使荷载直接作用于“空腔区”外围的块体上。解决爆炸荷载计算和加载的问题后，结合DDA程序，可进行爆炸成坑的模拟，模拟的总体流程如图1所示。本模拟用到的DDA程序由三个子程序组成:线条生成程序DL.exe、块体切割程序DC.exe和分析计算主程序 DF.exe。其中DL是DC的前处理程序，它可以通过输入少量的数据即可自动生成大量的线条，包括边界线、节理线、洞室边界线等在块体生成中需要用到的各种属性的线，生成的线的信息供DC使用;同样的，DC是DF的前处理程序，通过DL提供的各种属性的线的信息，生成带外部边界、内部洞室和材料属性的模型，并对模型进行切割剖分，形成块体系统，块体系统信息供DF使用;块体系统信息和外部荷载信息以及时步控制的数据文件读入分析计算主程序DF进行计算，计算过程以图形实时显示。本文所用DDA程序为石根华博士提供。

图1 总体流程图

2 爆轰产物状态方程

爆轰产物的状态方程分为两类:一类与化学反应有关，称为显含化学反应状态方程，广泛用于爆轰的热力学计算，又叫热力学状态方程;另一类不处理化学反应，称为不显含化学反应状态方程，广泛应用于爆炸力学数值计算，在爆炸效应数值模拟方面取得比较满意的效果，又叫动力学状态方程［6］。典型的动力学状态方程是JWL(Jones-Wilkins-Lee)状态方程，它能描述爆轰产物的压力—比容—内能(p—V—E)的关系，广泛应用于数值模拟中，其表达式为:

其等熵方程为:

其中，p为压力;E为爆轰产物单位体积的内能;V为爆轰产物的相对体积(即爆轰产物体积与装药体积之比);A，B，C，R1，R2，ω均为材料常数，需通过圆筒试验标定得到。

JWL状态方程这6个系数随着炸药种类和装药密度的变化而变化，要标定出各种炸药在不同装药密度下爆轰产物的状态方程，必须做大量的圆筒试验，从工作量而言非常困难。针对这一问题，薛再清［7］提出了通用JWL(JWLG)状态方程，用单位质量装药爆轰产物体积Vm代替爆轰产物相对体积V，适用于不同装药密度，其表达式为:

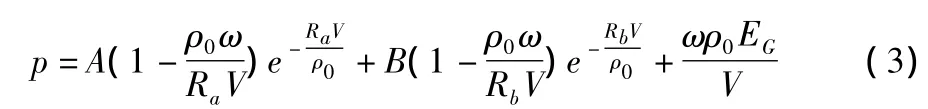
其等熵方程为:

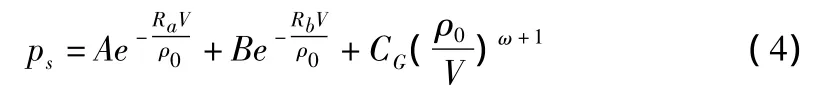
其中，p为爆轰产物压力;V为单位质量装药爆轰产物体积;EG为单位质量炸药的爆热;ρ0为装药密度;A，B，CG，Ra，Rb，ω 均为待定系数。

3 预设“空腔区”的计算

文献［8］中认为空腔半径R1与爆炸能量近似成正比，依赖于爆炸能量及介质的性质，包括其可压缩性和强度，其计算可采用如下公式:

其中，ρ为介质的密度;c0为介质中声波波速;fc为介质的单轴抗压强度;Q为炸药的能量;β=0.61。破碎区半径Rd与空腔半径成正比:

破碎区是指岩体在爆炸荷载作用下发生粉碎性破坏的区域，本文中爆炸成坑模拟时，直接忽略这一区域，预设“空腔区”半径根据破碎区半径Rd取值。

4 爆坑模拟案例

取靶体材料为以下参数的凝灰岩:密度ρ=2.83×103kg/m3，岩体中波速 c0=5 870 m/s，单轴抗压强度 fc=114.5 MPa［9］。设药包半径a=0.1 m，为装药密度 ρTNT=1.65×103kg/m3的 TNT药包，能量密度 Q0=6.803 MJ/kg［10］，则炸药总能量:

将以上参数代入式(5)，式(6)，可得 R1=0.214 m，Rd=1.28 m，可见压碎区半径已接近药包半径的13倍，这一结果偏大，考虑到压碎区也不是完全变成粉末，碎屑也可以承担一定的压力，模拟时所需的空腔半径可在R1和Rd之间取值，取预设“空腔区”半径为0.60 m。

根据文献［7］，该TNT药包的JWLG状态方程的具体参数取值见表1。

表1 药包所用TNT的JWLG状态方程参数

将表1中的参数代入式(3)，式(4)可得爆轰产物气体在0.6 m空腔中产生的压力为2.464 MPa，设该荷载在20 μs衰减至0。

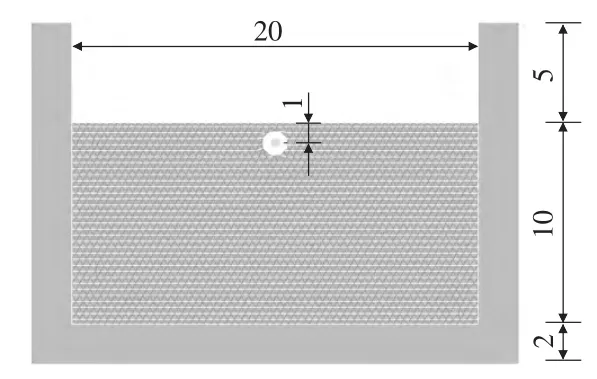
图2 模型示意图（单位：m）

建立的模型尺寸如图2所示，岩体尺寸为20 m×10 m，药包埋深为1 m，外部固定边界为内部尺寸20 m×15 m，外部尺寸24 m×17 m，宽2 m的“凹”形。

爆破漏斗的形成过程如图3所示，分别截取1 000步、2 000步和5 000步时的爆破漏斗瞬时状态。

图3 爆破漏斗形成过程

从该结果可以看出，用DDA进行爆炸成坑的模拟，由于预设了“空腔区”，从粉碎区外缘开始计算，此时爆炸作用相对于爆炸中心已经衰减不少，爆轰产物的压力不足以使围岩体破碎，而是沿着划分单元时划分出的节理面开裂。在接近自由面(原地面)的药包上方，块体被冲击力抛起，呈辐射状飞散。被抛出的块体一部分块体落回坑内，一部分落到原自由面(原地面)上，共同形成可见弹坑，可见弹坑的轮廓如图3c)所示。将图3c)与实际工程中观测到的弹坑形状对比可以发现，DDA模拟结果同样存在明显的回填物组成的区域以及开裂区，用DDA模拟的爆炸成坑效果与试验结果符合较好。