基于简化模型分析岩石第Ⅱ类曲线
2014-11-09孔繁越
孔繁越
(北京交通大学土木建筑工程学院,北京 100044)
1 概述
岩石的单轴压缩试验一直是确定岩石基本力学特性的一种方法,由于该方法操作简单,经常最先用来判断岩石的基本性质。1970 年,W.Wawersik 和 C.Fairhurst[1]将全程应力—应变曲线的类型分为Ⅰ类和Ⅱ类。第Ⅰ类岩石破坏传播过程是稳定的。第Ⅱ类岩石的破坏是不稳定的或者说是可以自持续的,见图1。
关于岩石第Ⅱ类曲线的真正存在性,国内外学者存在两种截然不同的观点。一派观点认为第Ⅱ类曲线的存在是可能的,这与岩石的不均一性,加载控制方式及加载速率等因素有关,并指出在加载方式为径向应变控制的情况下,出现第Ⅱ类曲线是完全可能的。并以两类曲线的不同来区分岩石是否属于脆性。另一派是以葛修润院士为代表的,认为第Ⅱ类曲线存在是由于采用的试验机不够先进,并且通过进行反复加载和卸载从而得到的第Ⅱ类曲线是不合理的,不应作为岩石固有的特性。
2 关于岩石第Ⅱ类曲线存在的观点
2.1 基于能量观点的分析
对于相同硬脆性岩石取样进行两种不同加载方式控制的试验。试验一以轴向控制得到第Ⅰ类曲线,试验二以径向控制得到第Ⅱ类曲线。对两类曲线能量变化进行分析可以导出以下公式:

可以发现E1>E2,由于硬脆性岩石达到峰值后破坏为自持续的,所以ΔE的能量将转化为动能,在实际试验一中加载的岩样都产生了爆裂现象。而采用更稳妥的径向控制试验,试件随径向速度的加载有一定的卸载,吸收岩样储存的应变能使得能量不转化为动能而稳定破坏,从而得到第Ⅱ类曲线。从能量的观点可以看出第Ⅱ类曲线形成的原因是储存的弹性势能在峰值之后的一种释放,能量足以维持岩石的破坏并产生轴向应变的回弹。
2.2 加载方式对岩石曲线形成的影响
想要得到两种不同类型的曲线,需要对岩石的单轴压缩试验的加载方式进行控制。若只是采用轴向加载,速率为0.001 mm/s,轴向应变是全程增加的,无法得到第Ⅱ类曲线。因为试件接近破裂之时,轴向应变的变化并不敏感,当采用轴向应变作为控制方式时,试件的破坏往往只是一瞬间的破坏,不能记录破坏的过程。因此要采用更加缓慢、稳妥的加载控制方式来延长破坏过程,从而来获得第Ⅱ类曲线。由于单纯轴向控制刻意约束了轴向变形发展的方向,所以不能合理的表现岩石破坏的机制。要想描绘第Ⅱ类曲线的全过程必须采用更加精细的加载控制方式。除了上述介绍的径向控制之外对于峰后加载方式还有以下几种形式:利用声发射率作为控制变量,用非弹性体积应变率作为反馈信号,以应力—应变的线性组合作为反馈信号等。这些方式都能更加精细、缓慢加载来表现岩石真实的破坏过程。
3 通过简化模型解释第Ⅱ类曲线的形成
对以上研究争论的总结不难看出,问题的关键在于脆性岩石的物理力学特性能否造成第Ⅱ类曲线所描述的破坏过程。我们不妨从高脆性岩石和低脆性岩石的受力变形本质出发,假想两种简化模型。一种是高脆性模型单元如图2所示,每一个单元为具有很大弹性的球体(如弹力球)。另一种为低脆性模型单元如图3所示,每一个单元为具有很大可塑性的球体(如橡皮泥球)。

图1 岩石第Ⅰ类 、第Ⅱ类曲线

图2 高脆性模型单元
图3 低脆性模型单元
高脆性岩石单元在受到外力时变形量小,外力功以弹性势能的形式储存在单元体内,而低脆性岩石单元则将外力功主要转化为单元的形变。下面将对两种岩石的单轴压缩过程进行描述,从而解释两类曲线产生过程。将岩石单轴压缩过程简化为三个阶段如图4所示,第一阶段为孔隙压密阶段,由于试验机开始加载,岩石岩样受到轴向外力作用后进入压密阶段,两个模型中的岩石小单元变得更加紧凑直到互相接触,如图5,图6所示,此过程轴向应变近似线性增加。
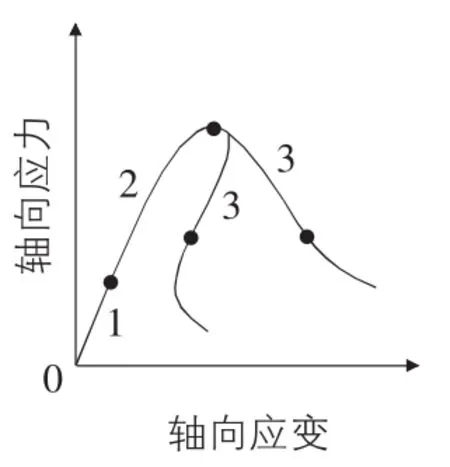
图4 单轴压缩三个阶段

图5 高脆性单元互相接触
图6 低脆性单元互相接触
随后岩石进入第二个阶段,为变形和局部破坏积累阶段。岩石小单元相互作用产生弹性变形及塑性形变并储存弹性势能,单元之间产生错动,由于高脆性岩石储存弹性势能较强,变形较小在模型上表现为小单元由球形变为两极略扁的椭球,因为弹性势能的存在单元之间相互有很强的作用力,很像压在一起的气球,如图7所示。而对于低脆性岩石,外力做功很大程度上转化为了弹塑性变形,模型上变形为被压得很扁的椭球,而且单元之间的相互作用力较小,很像压在一起变了形的一些橡皮泥球,如图8所示。

图7 高脆性单元互相挤压
图8 低脆性单元互相挤压
随着荷载的增加最终到达峰值,此时单元中的局部破坏已经积累到极限进入下一个阶段——峰后破坏阶段。在高脆性岩石中表现为弹性势能积累到达极限,小单元有释放弹性势能并破裂分解成更小单元的趋势。而低脆性岩石表现为小单元塑性变形到达极限,小单元有形成更大的相互滑移错动形成断裂的趋势以及分成更小单元的趋势。此时考虑不同加载方式对高脆性岩石峰后段曲线的影响。当仍就按轴向位移控制时,由于岩石轴向位移单调增加,约束了轴向位移发展的方向,因此岩石内各单元的弹性势能不能以轴向回弹的形式释放,只能以径向及分解成小单元的形式释放。产生较大的应力跌落,甚至可能导致岩石岩样发生爆裂。由于该过程轴向应变一直是单调增加的,因此得出的曲线为第Ⅰ类曲线,模型变化示意图如图9所示。当加载方式变为径向位移控制时,轴向位移的约束解除,单元内的弹性势能便可以沿轴向方向释放,表现为轴向应变的回弹并伴随着单元分解为更小的单元,同样伴随产生较大的应力跌落。此过程的曲线即为第Ⅱ类曲线,具体模型的变化过程如图10所示。对于低脆性的岩石来说,由于单元之间没有较大的弹性势能,峰后的进一步破坏仍然需要外力继续做功,使得单元进一步分解并相互错动最终形成断裂带从而破坏。此过程应力跌落缓慢且平滑,破坏过程相对稳定,形成标准的第Ⅰ类曲线,模型的具体变化过程如图11所示。

图9 第Ⅰ类曲线模型的变化过程
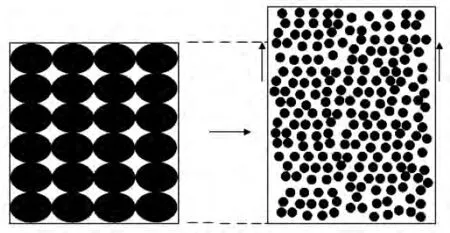
图10 第Ⅱ类曲线模型的变化过程Ⅱ

图11 第Ⅰ类曲线低脆性模型的变化过程Ⅰ
通过以上的简化模型可以形象、直观的理解第Ⅰ类曲线和第Ⅱ类曲线产生的过程。由于只是对两种曲线产生机制的定性判断并未进行数学模型的构建。从以上的解释可以得到以下结论:
1)在岩石单轴试验全程应力—应变曲线中,既可能存在第Ⅰ类曲线也可能存在第Ⅱ类曲线,这与试件岩石脆性、试验机加载控制条件等因素有关。2)岩石第Ⅱ类曲线峰后段的破坏无需试验机对其做功,其自身在峰值前期储存的弹性势能就能满足破坏发展的条件。3)采用轴向控制对高脆性岩石试样进行加载,由于约束了其轴向变形发展方向使得岩石的破坏被迫的沿径向产生爆裂。这样的加载方式违背了岩石本来的破坏形式,得到的第Ⅰ类曲线实际意义不大。
4 基于简化模型对不同形态第Ⅱ类曲线的解释
有关学者通过研究发现,第Ⅱ类曲线岩石的不均匀程度往往影响第Ⅱ类曲线峰后段的形态。对于岩石的均质性比较好的,峰后曲线的曲折较少,而对于曲折很多的峰后曲线,则说明岩石的不均质程度很高,岩石完全破坏所需要的反复过程较多。
此现象基于上部分所用的简化模型可以做如下解释:对于曲线1均质性好的岩石(见图12),我们可以直接参照上部分所叙述的采用径向控制的第Ⅱ类曲线获得,该过程已经假设脆性岩石的均质性很高。对于曲线2均质性不好的岩石(见图13),我们采用图14的模型进行解释。

图12 曲线1
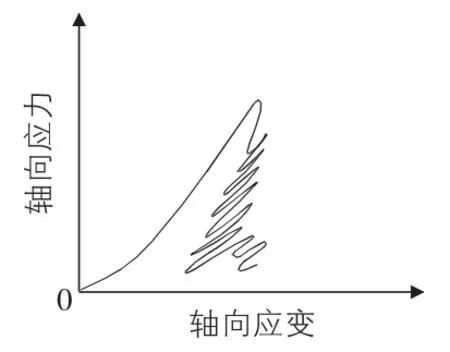
图13 曲线2
假设在高脆性岩石中混有不均匀的低脆性岩石,加载的第一步过程与之前相同,单元之间的孔隙减小如图15所示。随着加载的继续进行,高脆性单元开始储存弹性势能而低脆性的单元则发生较大的变形,如图16所示。

图14 曲线2模型解释示意图

图15 曲线2模型解释步骤一

图16 曲线2模型解释步骤二
当达到峰值后高脆性单元变形储能达到极限,有释放弹性势能和分解成小单元的趋势,而且掺杂在其中的低脆性的单元也达到了变形极限,有分解成小单元的趋势。由于低脆性单元的存在导致岩石单元间的应力分布不均,有的单元较早达到极限,因此在峰后段有一部分单元首先释放能量并分解,如图17所示,在图13中表现为峰后应力下降应变轴向回弹段。经过一部分单元能量的释放,岩石中又有了孔隙并且各单元又具有了一定变形和储能的能力,因此继续加载导致轴向位移增加应力有所回升直到各单元再次达到极限,如图18所示,在图13中该过程表现为峰后曲折段的应力和应变都增加的部分。随着加载的进行又有一批单元达到极限,如此反复,就形成了如图13曲线的形状。这也说明了峰后曲线产生反复折线的原因。

图17 曲线2模型解释步骤三

图18 曲线2模型解释步骤四
5 岩石第Ⅱ类曲线在工程中的应用
经过以上的研究,我们发现具有很强脆性的岩石在峰后段表现为第Ⅱ类曲线破坏。常见的脆性岩石有花岗岩、凝灰岩、闪长岩、变质砂岩、盐岩、板岩及其变质岩体。由于第Ⅱ类曲线岩石的特性,在受到外荷载达到峰值应力时可能出现岩爆危险。因此作为围岩的第Ⅱ类岩石在达到应力峰值后,岩石中储存的弹性势能足以使破坏发展,又因为开挖围岩没有来得及支护,最终导致岩石发生不稳定的破坏。
通过对围岩岩性的判断并基于第Ⅱ类曲线峰后特性的研究,以第Ⅱ类曲线岩石为围岩的隧道施工中可能出现安全、工期、投资等各方面风险。施工中要采取相应措施降低以上风险,并针对各项风险因素拟定初步处理方案,将各类风险降到可接受的水平,而且在施工中应做好相关风险防范工作。这也是对第Ⅱ类曲线深入研究的意义所在。
6 结语
1)岩石第Ⅱ类曲线峰后段产生应变回弹的实质是脆性岩石在压缩过程中储存了足以满足破坏发展的弹性势能。使得脆性岩石可以自持续的破坏,当选择不约束轴向应变变化的加载方式(如径向控制)加载时能够清楚的得到第Ⅱ类曲线。
2)通过简化的球状模型对第Ⅰ类曲线和第Ⅱ类曲线的产生实质进行解释,证明第Ⅱ类曲线的存在是合理的。并就不均匀性对第Ⅱ类曲线的影响进行分析,均质性好的岩石曲线峰后曲折较少,不均匀的岩石峰后曲线曲折较多。
3)岩石第Ⅱ类曲线反映了脆性岩石压缩破坏的本质,对隧道工程中的岩爆危险预测起到重要的作用。
[1]Wawersik W,Fairhurst C.A study of brittle rock fracture in laboratory compression experiments[J].International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts,1970(7):561-575.
[2]王明洋,严东晋.岩石单轴试验全程应力应变曲线讨论[J].岩石力学与工程学报,1998,17(1):101-106.
[3]郑 宏,葛修润,李焯芬.脆塑性岩体的分析原理及其应用[J].岩石力学与工程学报,1997,16(1):8-21.
[4]潘一山,徐秉业,王明洋.岩石塑性应变梯度与Ⅱ类岩石变形行为研究[J].岩土工程学报,1999,21(4):471-474.
[5]郑 宏,葛修润,李焯芬.对“岩石单轴实验全程应力应变曲线讨论”的回复[J].岩土工程学报,1998,17(1):107-108.
[6]潘一山,宋义敏.对“岩石塑性应变梯度与Ⅱ类岩石变形行为研究”讨论的答复[J].岩土工程学报,2000(2):263.
[7]柯长仁,葛修润,蒋俊玲.基于虚内键模型的岩石单轴压缩全过程曲线模拟[J].岩土力学,2009,30(5):1509-1514.
[8]尹小涛,葛修润,李春光.加载速率对岩石材料力学行为的影响[J].岩石力学与工程学报,2010,29(1):2610-2615.
[9]潘鹏志,周 辉,冯夏庭.加载条件对不同尺寸岩石单轴压缩破裂过程的影响研究[J].岩石力学与工程学报,2008,27(2):3636-3642.
[10]潘鹏志,周 辉,冯夏庭.岩石Ⅰ类和Ⅱ类曲线形成机制的弹塑性细胞自动机分析[J].岩石力学与工程学报,2006(10):3823-3829.
