巨型钢框架—索支撑结构中索突然失效的响应

马 波 朱佳锋 王 飞

(1.上海艾能电力工程有限公司，上海 200023;2.江苏科技大学船建学院，江苏镇江 212003)

0 引言

巨型钢框架—预应力索支撑体系将V形预应力索支撑引入到竖向钢结构体系中，预应力拉索除了参与抵抗侧向荷载，还作为巨型梁支座起支撑作用。分析表明，此结构体系大大提高了钢框架结构的侧向刚度，且梁的受力性能得到改善［1，2］。预应力索内蕴很大的变形能，在偶然荷载作用下，索的突然失效对结构的影响不容忽视。一方面，拉索中积蓄的应变能在断索瞬间得到释放，必会对结构造成冲击;另一方面，拉索断裂后结构原先的平衡状态被打破，对其他构件必然造成很大影响。近年来，结构关键构件的失效所引起的易损性及连续倒塌问题得到了极大重视［3-5］，但对索支撑的巨型钢框架中索的断裂问题研究较少。

索的突然破断过程分析牵涉到几何、材料非线性，及结构几何组成变化带来的状态非线性，且初始动力响应由几何组成变化所引起，与常规由外动荷载或位移输入引起的动力反应分析有本质不同，利用传统的有限元方法难以准确模拟和追踪其失效全过程。

向量式有限元方法(VFIFE)是由丁承先等［6］提出的一种基于向量力学的新计算方法，它从质点运动方程出发，不形成整体刚度矩阵，因而无矩阵奇异的问题，非常适合于几何形态变化的非线性问题。国内喻莹等［7］将VFIFE引入桁架结构的倒塌分析，取得了较好的效果。本文采用向量式有限元法对巨型钢框架—索支撑结构在偶然荷载下的突然断索的响应全过程进行模拟分析。

1 向量式有限元简介

向量式有限元法［8］是一种基于向量力学的全新数值计算方法。它用一组空间质点近似描述所分析的结构，以牛顿第二定律描述质点的运动。在时间上将运动历程划分为一系列途径单元，单元间运动可不连续。内力计算时采用逆向运动获得纯变形。运动的求解采用显式积分公式。

1.1 结构动力反应分析

VFIFE本质是一种动力模拟方法。对自由质点α，其位移可由牛顿运动方程式求得:

其中，Mα为质量矩阵;为质点加速度;为外力向量;为内力向量;为阻尼力为阻尼系数，为质点速度。

由中央差分公式，可得到运动方程的解为:

其中，dn－1，dn和dn+1分别为质点在第 n －1，n 和 n+1 时间步的位移向量;Δt为时间步长。

1.2 预应力索行为模拟

索单元与一般杆单元不同的是它可能含有预应力。对于一个既定的含预应力索钢结构，能够确定的只有初始态几何参数和各索杆的初始内力值。VFIFE引入预应力的方法直接、简便，将预应力作为初始态存在的力直接参与计算，不用找形和找力就能建立初始态模型进行静力分析。此预应力不需经过特殊的处理，可视为单元的初始内力，节点上的合力为0，结构处于自应力平衡状态。当索拉力不大于0时取为0，模拟索的松弛。

1.3 断裂模拟

VFIFE假设在破断点产生一个新的质点，重新计算质量及内力分配。在破断瞬间单元内力得到继承，只是单元连接关系发生改变，之后继续计算结构的受力与变形，结构的初始内力和变形未被忽略，能真实有效跟踪结构响应的全过程，向量式有限元法的提出为研究结构的全过程变化开辟了一条新途径。

2 索突然失效响应全过程

基于MATLAB软件编写向量式有限元程序可用于断索失效全过程分析，利用MATLAB强大的数据处理能力能实时地记录结构断索后整个振动过程质点坐标及内力变化，程序计算结果简单、直接，只需具备简单数据处理及绘图功能的软件即可处理。

2.1 计算模型

计算选用的典型巨型钢框架—拉索支撑结构其平面尺寸为36 m×36 m，总高度达108 m，层高4 m，除顶部大层为4层，其余大层为7层，共18层。在结构的四角布置四个6 m见方的格构式巨型柱，每个巨型柱都是由四根箱形截面柱通过柱间人字形支撑相连而成。沿结构高度方向每隔36 m设置四根巨型立体桁架梁使其与巨型柱相连。每个巨型梁都为一个楼层高，由四根工字形弦杆及竖向、斜向腹杆组合而成。图1a)给出了此结构的平面图。主要钢构件采用Q345B，并引入理想弹塑性模型;拉索采用极限抗拉强度为1 870 MPa的钢绞线。利用对称性取结构其中一榀框架，将其简化为平面模型进行分析，如图1b)所示。巨型框架构件的截面尺寸如表1所示。

竖向恒荷载为4.5 kN/m2，活荷载为2.5 kN/m2。基本风压取0.4 kN/m2，地面粗糙度B类，将由荷载规范算得的风荷载由左至右反对称施加在巨型柱外侧柱肢上。在荷载工况“1.2恒+0.2活+0.2风”［9］作用下，设各大层右侧索分别破断，分析断索对结构的影响。

图1 结构计算模型

表1 构件的截面尺寸 mm

巨型钢框架—拉索支撑结构拉索截面面积以“水平荷载作用下，结构的最大层间位移不超过楼层高度的1/400”为确定准则;拉索初始预拉力由“最不利工况下，受压预应力拉索剩余拉力接近零”及“正常使用状态下，巨型梁的变形满足规范要求且不出现反拱”双重准则确定。拉索的直径和预拉应力见表2。

表2 拉索的直径和预拉应力

有限元模型中每根杆划分为单个梁单元，每根索划分为单个索单元。索力小于0时拉索发生松弛。整个分析过程分为两个阶段:索破断前(0 ms～1 ms)结构承受竖向荷载、风荷载及预拉力组合作用，处于静力平衡状态;之后拉索突然断裂，分析1 ms～600 ms的结构响应。运动方程中的阻尼比按Rayleigh阻尼计算确定，时间步长取0.15 ms。

选巨型梁端、柱端的杆件及索，考察断索前后其内力的变化，构件位置如图2所示。为与VFIFE结果进行对比，采用通用有限元软件ANSYS对断索后最终平衡态进行分析，并定义不考虑初始侧移时断索振动过程中最大位移值与断索后最终平衡态位移值之比为动力系数βd，定义不考虑断索前内力时断索后振动过程中最大内力与断索后最终平衡态内力之比为动内力系数β。

图2 构件编号

2.2 各大层水平位移

S1～S3(见图1b))分别破断时的各大层侧移时程曲线如图3所示。可看出，断索所引起的各大层水平位移的波动幅度均不大，位移的增大主要因断索后刚度突变产生。底层索S1断裂后结构顶点侧移约为48 mm，最大层间侧移约为35 mm，发生在底部大层;中间层索S2断裂后结构顶点侧移约为54 mm，最大层间侧移约为26 mm，发生在中间大层;顶层索S3断裂后结构顶点侧移约为84 mm，最大层间侧移约为30 mm，发生在顶部大层。上述位移均满足JGJ 99-98高层民用建筑钢结构技术规程［10］要求。

图3 不同位置索断后各大层侧移曲线

S1～S3分别破断时的各大层侧移的动力系数βd及在断索始末的比值d2/d1见表3。从表3可知，βd最大仅为1.06，d2/d1最大为4.05，都发生在顶大层右侧索S3断裂时。

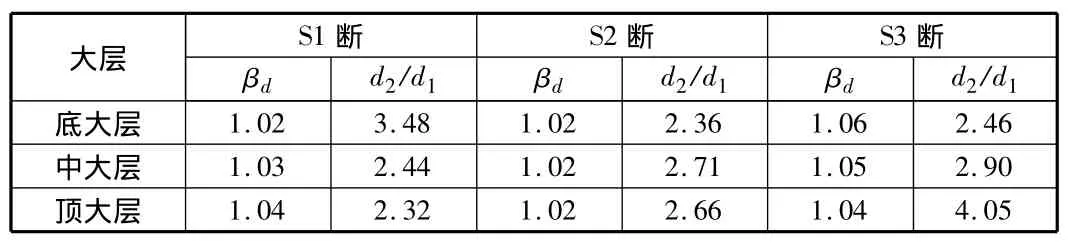
表3 不同索断裂引起的各大层侧移变化

2.3 构件动内力

图4分别为底大层索S1突然断裂后左柱底端右柱肢、柱间斜撑和横杆的轴力曲线。S1突然失效后，底层左柱肢的轴力振荡幅度很大，断索冲击引起的轴力变化程度大于由于结构几何组成变化引起的内力重分布所带来的变化。但柱肢间斜撑和横杆在断索卸载冲击下由荷载动效应引起轴力变化幅度不如由内力重分布所引起的轴力变化。柱间斜撑和横杆的波形相似，但前者加载而后者卸载，因二者要满足同一节点水平力的平衡条件。各杆件均在0.2 s左右趋于静止。

图5给出了底层拉索S1突然破断后与断索相连的巨型梁端上弦杆和斜腹杆的轴力时程曲线，两者均先卸载再加载。从内力重分布角度分析，底层索S1断对上弦杆的轴力影响较大，对腹杆的影响较小。从动效应角度看，上弦杆振幅不大，斜腹杆振幅较大。

图6为底层索S1突然破断后中间大层索S2的轴力变化曲线。S2的轴力振荡十分明显，波幅较大，0.2 s后趋于静止，而内力重分布效应对索轴力影响不大。整个过程中，索始终未发生松弛。

表4给出了底大层右侧索S1突然破断后，各个构件断索前轴力F1、断索后平衡态轴力F2、振动过程轴力最大值Fmax、动内力系数β及断索前后静止状态下轴力的比值F2/F1，并将VFIFE与ANSYS分别计算得到的F2做了对比，发现两者很接近。底大层索S1突然失效后，底层柱肢及靠近断索位置的上层索S2、巨型梁端斜腹杆的动内力系数都大于1.2，其他杆件均接近1。断索引发的振动停止后，与断索前相比轴力变化较大的有底层巨型柱肢间横杆、斜撑及靠近断索位置的巨型梁端上弦杆，其他杆件变化不大。总的来说，表4中的杆件由底层索断引起的内力变化都超过了20%，巨型梁端斜腹杆和索S2的轴力几乎为原来两倍。索强度很高，一般有很大富余，不必担心其拉断。但腹杆设计时应考虑断索后果，否则会发生破坏，并进一步导致巨型梁失效。

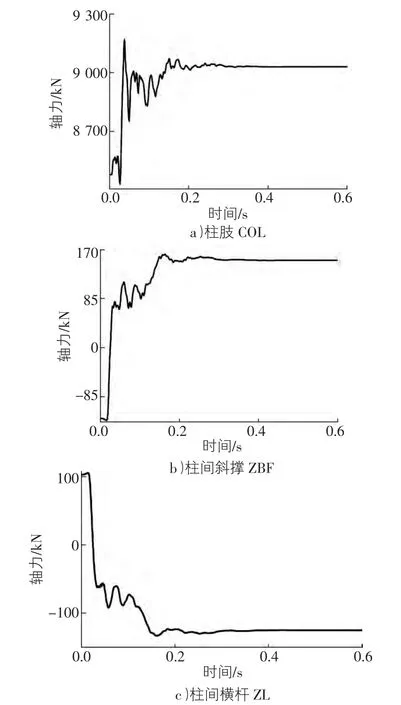
图4 底层索S1断后巨型柱构件的轴力曲线

图5 底层索S1断后巨型梁构件的轴力曲线

2.4 断索位置对内力的影响

表5给出了中间大层索S2突然断裂后的构件轴力变化，可以发现动内力效应并不大，几乎可忽略。与索S1失效时相同，巨型柱肢间横梁、斜撑和巨型梁端弦杆的轴力在断索前后变化较大。在断索过程中，轴力增加最大的为巨型梁端弦杆，超过断索前轴力的60%，当引起重视。

表6列出了顶大层索S3突然断裂后构件轴力变化。结果表明，除巨型柱柱肢动内力系数较大外，其他杆件的动内力系数不超过1.1。与其他层索断后一样，也是巨型柱肢间横杆、斜撑及巨型梁端弦杆的轴力变化较大。即使梁端上弦杆和断索不在同一层，其轴力还是增加了30%。

图6 底层索S1断后中间层右侧索的拉力曲线

表4 底大层索S1断对各构件轴力影响

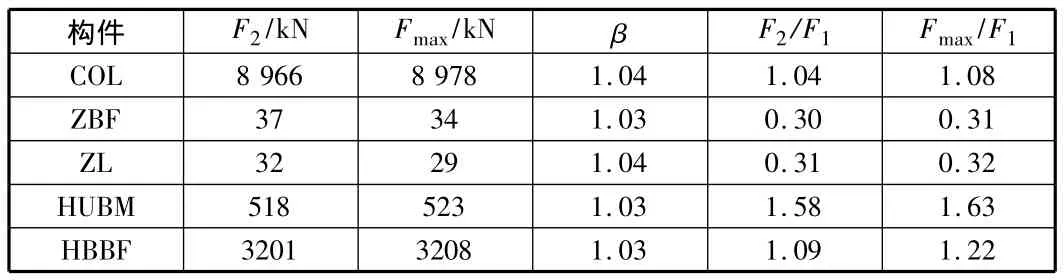
表5 中间大层索S2断对构件轴力影响

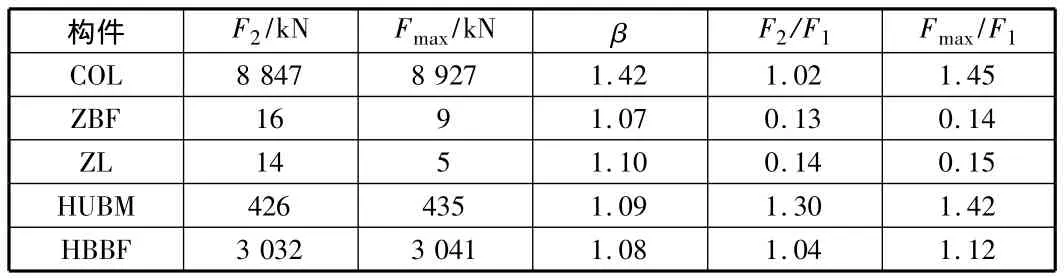
表6 顶大层索S3断对构件轴力影响

3 结语

1)向量式有限元能很好地模拟预应力巨型钢框架结构中索突然断裂的动力效应，其优势在于施加预应力简单以及无需重分网格就能模拟断裂产生的状态非线性，这是传统有限元方法所不具备的。另外，由于向量式有限元的特点，无需求解矩阵方程并可随时改变质点之间的关联，轻易用单一流程即可模拟结构从连续到不连续的过程。

2)顶层索突然断裂引起的巨型钢框架—拉索支撑结构顶点水平位移最大，但无论哪层索断，各大层侧移的动力系数均只稍大于1，意味着断索前后结构位移变化主要源自支撑刚度的突变。

3)索突然断裂，巨型钢框架—拉索支撑结构中索的动内力系数接近2，断索引起的动效应不能忽略。断索位置对构件的动内力系数影响较大，且不同断索位置导致结构不同的内力重分布，因此，设计时应考虑不同预应力组合，才能确保断索后结构的安全。

［1］唐柏鉴，彭小龙，邵建华.巨型钢框架—拉索支撑体系的Pushover分析［J］.工业建筑，2013，43(3):120-124.

［2］马 珺，唐柏鉴.巨型钢框架—拉索吊挂结构拉索参数确定方法［J］.力学与实践，2012，34(6):23-26.

［3］Mozos CM，Aparicio AC.Numerical and experimental study on the interaction cable structure during the failure of a stay in a cable stayed bridge［J］.Engineering Structures，2011，33(8):2330-2341.

［4］Kim J，Kim T.Assessment of progressive collapse-resisting capacity of steel moment frames［J］.Journal of Constructional Steel Research，2009，65(1):169-179.

［5］王 飞，唐柏鉴.单层平面钢框架预应力索突然失效的动力效应分析［J］.钢结构，2013，28(4):25-28.

［6］Ting E C，Shih C，Wang Y K.Fundamentals of a vector form intrinsic finite element:Part I.Basic procedure and a plane frame element［J］.Journal of Mechanics，2004，20(2):113-122.

［7］Yu Y，Paulino G H，Luo Y.Finite particle method for progressive failure simulation of truss structures［J］.Journal of Structural Engineering，2010，137(10):1168-1181.

［8］卢哲刚，姚 谏.向量式有限元——一种新型的数值方法［J］.空间结构，2012，18(1):85-91.

［9］General Services Administration.GSA 2003.Progressive collapse analysis and design guidelines for new federal office buildings and major modernization projects［S］.USA:General Services Administration，2003.

［10］JGJ 99-98，高层民用建筑钢结构技术规程［S］.