一种判别多梁桥横向连接弱化的新方法

李自华

(河北省高速公路京秦管理处，河北秦皇岛 066000)

桥梁的横向分布系数对于判别桥梁构件的空间状态具有非常重要的意义。一般来说，整体性好的桥梁，其横向分布系数往往较小;反之，整体性较差的桥梁，其横向分布系数会比较大。在工程实践中，一般的钢筋混凝土和预应力混凝土梁式桥往往需要根据桥梁工程的施工过程特点、构造设计等的不同采取不同类型的横向结构。因此，对于各种不尽相同的横向结构类型，必须以相应的横向结构简化计算模型为基本，从而用相应计算方法进行计算，进而使得荷载横向分布的计算能更好地适应各种类型的结构特性。

本文首先针对一类具有代表性的典型的荷载横向分布计算方法——(修正)偏心压力法，给出一种新的公式计算方法;然后，给出一种基于相邻横向分布系数差的横向连接判别指标，并给出了该指标的判别依据。

1 一种偏心压力法横向分布系数的新算法

通过分析归纳总结桥梁结构受荷之后各纵向主梁的变形(比如挠度)规律，我们可以观察到，这些主梁在上述启程荷载作用下所处的受力状态几乎就与我们所用的一般材料力学中杆件的偏心受压的受力情况高度的类似。因此，我们将桥梁空间结构中横梁简化为刚性梁，且将这些刚性梁都被简化为刚支撑在各片主梁上面的连续刚体，从而来计算荷载的横桥方向的分布系数，这种方法被称为“偏心压力法”。又鉴于我们在上述方法中采取了桥梁的空间结构中的横隔梁的刚度为无穷大的假设，因此这种方法也被称作“刚性横梁法”。

刚性横梁法作为梁格法中的一个比较常用且典型的特例，它把待分析计算的梁桥结构简化成了梁格系模型进行分析和计算，而这个梁格系是由纵桥方向的主梁和与之相交的横桥方向的横梁所共同组成的，时间在桥梁结构上的荷载是通过该模型中的横梁，从某一纵向主梁传递到其他的纵向主梁上面去，而且与此同时，这些纵桥方向的主梁又对这些横桥方向的横梁提供了弹性支撑，从而使得它们具有协同工作的能力。刚性横梁法是刚接梁法的一种极端情况，也就是说，如果在刚接梁法中为横梁的抗弯惯矩设定一个较大数值即为“刚性横梁法”。

1.1 桥梁模型

本文采用偏心压力法以及修正偏心压力法对公路桥梁荷载横向分布特性进行研究时，所采取的桥梁模型是由n片主梁构成的简支梁桥，该简支梁桥横截面如图1所示。

主梁编号依次为1号、2号、…、N号，相邻两片主梁之间的间距为l0。

1.2 横向分布系数的新算法

1)只受一个荷载作用的情况。

设上述桥梁结构仅受到一个单位荷载P=1的作用，其作用位置在梁跨中，作用点距离1号主梁(边梁)轴线为x。第i号主梁轴线到桥梁横截面的中点的距离记作梁位ai。则其计算简图如图2所示。

如果采用偏心压力法对该结构进行计算，对于任意一片主梁(记为i号主梁)，其荷载横向影响线的两个控制竖标值ηi1和ηin分别为:

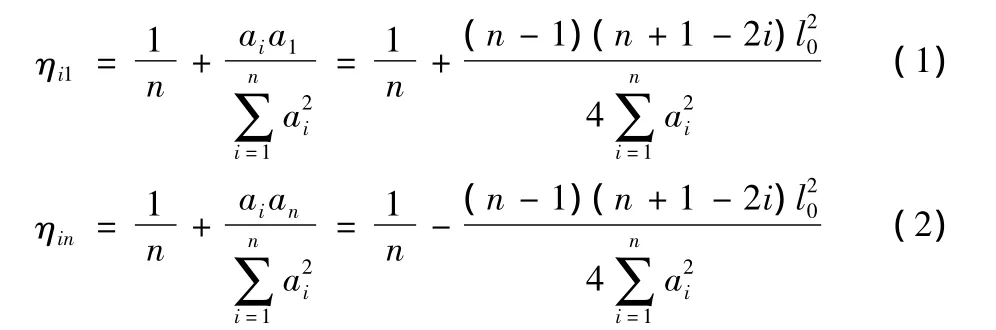
荷载横向分布影响线竖标值ηi为:

其中，x0i为影响线零点位置。将式:代入式(3)，得i号主梁荷载横向分布影响线竖标值ηi的表达式:

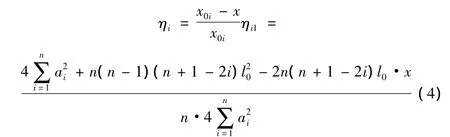
由于桥梁只受一个荷载的作用，且作用点距离1号主梁(边梁)轴线为x，因此上述ηi的表达式即为i号主梁所承受的荷载横向分布系数mi的表达式:

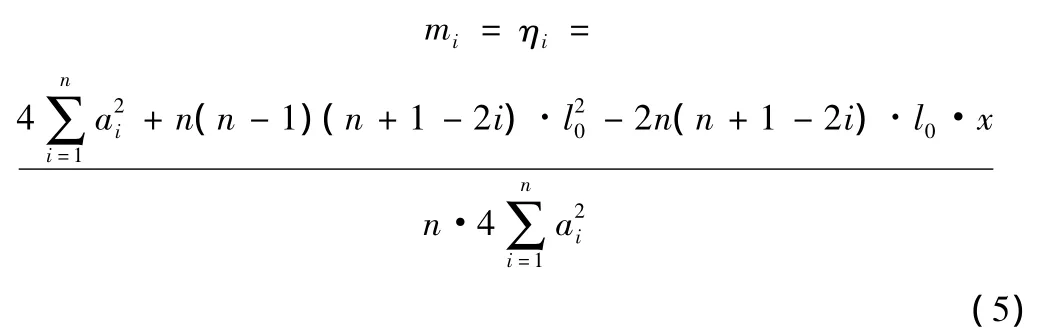
由式(5)可进一步得到i号主梁和i+1号主梁所承受的荷载横向分布系数其变化率的绝对值为:

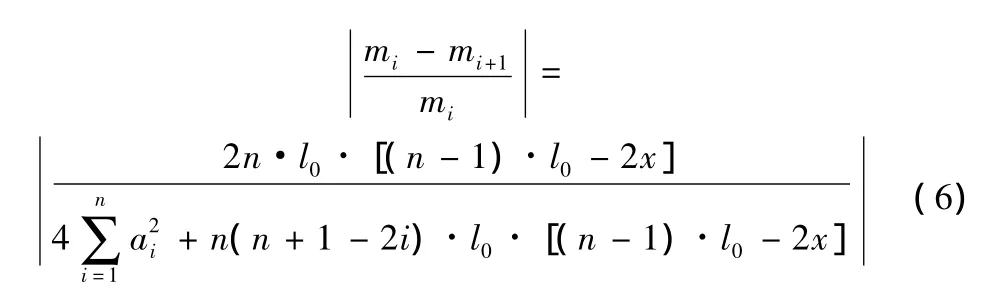
2)受到多个荷载作用的情况。

设图1所示桥梁受到k个单位荷载的作用，且其作用位置依然在桥梁的跨中位置，作用点到1号主梁(边梁)轴线的距离分别为 x1，x2，…，xk－1，xk。梁位 ai为桥梁横截面中点到 i号主梁轴线的距离。计算简图如图3所示。

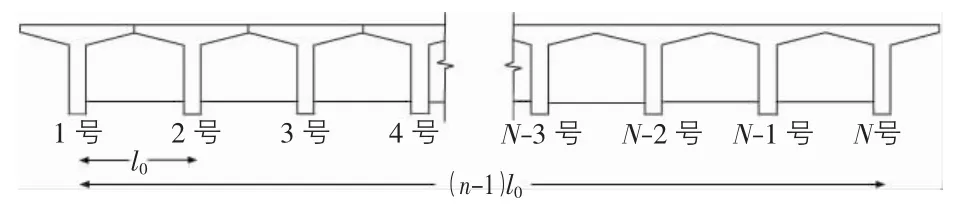
图1 桥梁模型横截面示意图

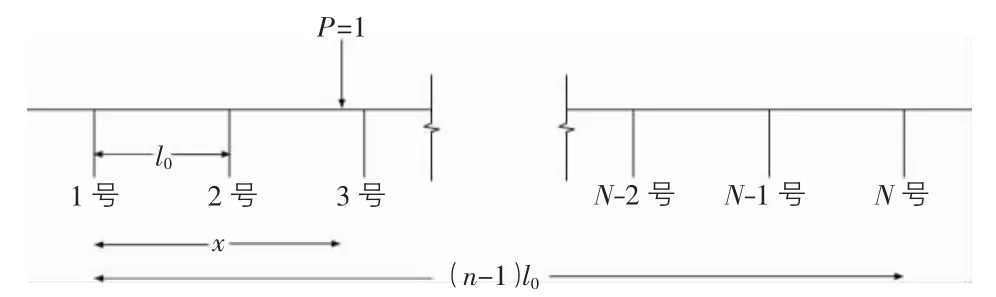
图2 桥梁只受到一个荷载作用的情况

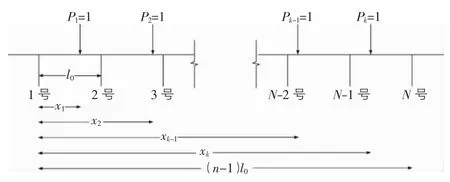
图3 桥梁受到多个荷载作用的情况

采用偏心压力法进行计算，对于任意一片主梁(记为i号主梁)而言，其荷载横向分布影响线竖标值ηi的表达式不变，仍为式(4)。i号主梁所承受的荷载横向分布系数mi为:

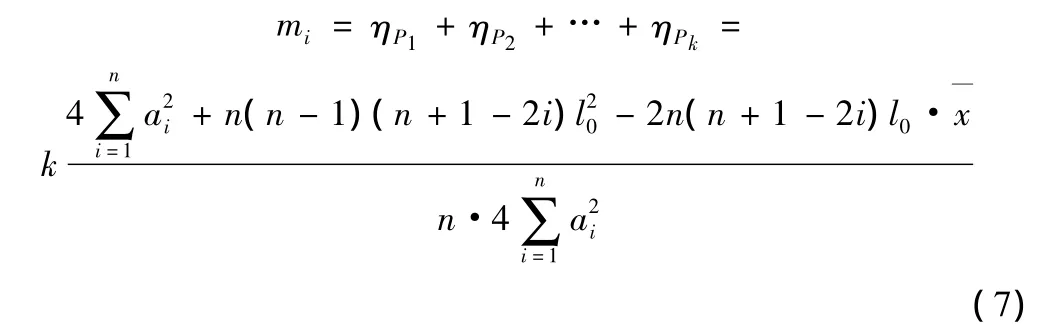
任意两片相邻主梁的荷载横向分布系数变化率的绝对值为:

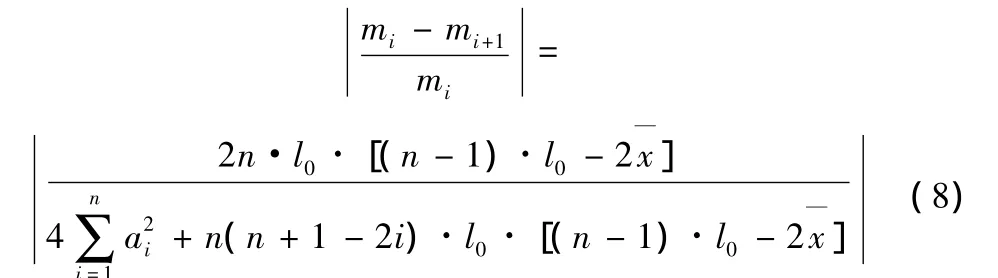
2 基于相邻横向系数变化率的状态指标

当采用偏心压力法计算桥梁的荷载横向分布系数时，可直接使用式(5)和式(7)求解，而不再需要通过以往的先绘制横向影响线、再求解横向分布系数的过程来计算。

分析式(6)和式(8)，得出如下结论:

因此，当0.5(n－1)·l0时(这样能保证i号主梁和i+1号主梁处于桥梁的同一半幅，而且是荷载所在的那一半幅，亦即1号主梁所在的那一半幅)在自变量的前述定义域内，函数在x=0处取到最大值，得:

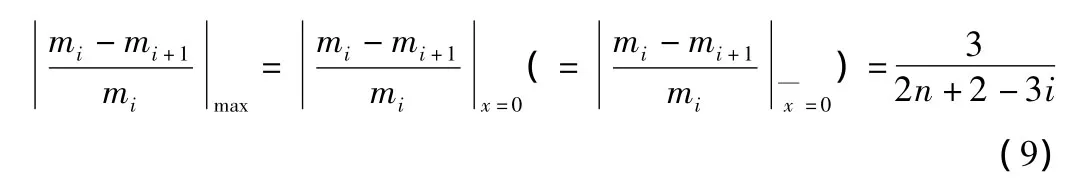
综上所述，当采用偏心压力法进行荷载横向分布的相关计算时，对于一座由n片主梁构成的简支梁桥，不论它是受到一个荷载的作用还是受到多个荷载的作用，只要荷载或平均作用距离荷载作用于目标主梁(即i号主梁和i+1号主梁)所在的那半幅桥面上，那么这两片相邻的目标主梁所承受的荷载横向分布系数其变化率之内。因此，当进行测试时，如果相邻横向系数变化率超出上述范围，可以初步断定为横向联系弱化或异常，进而判断铺装层退化。这就是从横向系数角度给出的桥梁状态判别方法。

［1］姚玲森.桥梁工程［M］.第2版.北京:人民交通出版社，2008.

［2］河北省京秦高速公路管理处，同济大学.基于管养目的的公路桥梁健康监测关键技术研究［Z］.2008.

［3］武修雄.考虑横梁刚度的横向分布系数的计算［J］.水运工程，1998(5):1-3.

［4］陈 可，崔亚楠，吕建鸣.荷载横向分布系数计算问题的研究［A］.中国公路学会桥梁和结构工程分会，2005年全国桥梁学术会议论文集［C］.2005:1118-1127.

［5］曾 智.混凝土桥梁铺装层受力分析和横向分布系数计算［D］.武汉:武汉理工大学，2004.

［6］李淑芬，钱永久，马艳峰.荷载横向分布计算方法比较分析［J］.湖南工程学院学报，2007，17(1):84-87.

［7］陈宇新，窦玉秋，韩伟峰.浅析简支梁桥横向分布系数计算［J］.东北公路，2003(3):94-96.