基于分形理论的路基填石料粒径优劣分析
2014-11-09吴安泽
吴安泽
(重庆交通大学交通运输学院,重庆 400074)
0 引言
具有自相似性和标度不变性的系统称为分形系统,随着分形理论的产生和发展,逐步的形成了分形几何学。分形理论作为一门新兴的横断学科,是非线性科学的前沿和重要分支。在物理化学、材料学科、地质勘探、信息科学等研究领域中十分活跃,是研究自然界和非线性系统中出现的不光滑和不规则几何形貌及复杂物理现象的有力工具,数学基础是分形几何[1]。同其他数学概念一样,分形是从客观存在的形和数的关系中抽象出来的。自然界中广泛的存在分形。
分形维数简称分维,是描述分形的数量特征的主要参数,其用于研究形态不规则的事物,度量复杂形体的不规则性。分形形体中的自相似性可以是完全相同,也可以是统计意义上的自相似性[2]。作为分形中的参量,分形维数最早由 Hausdorff提出,以Hausdorff度为基础,维数可以是非整数及分维。随着分形理论的逐步发展,其越来越多的用于岩土工程碎石填料的分析中。
1 碎石料的分形特征
在爆破力和碾压作用下,岩石形状虽然不完全相同,但经统计发现都至少存在一个近似的三角形面。岩石的破碎过程类似于Koch曲线。先将直线段三等分,然后将中间部分用等边三角形代替,依次重复以上两步便会形成Koch曲线。Koch曲线虽在直线段的细部发生变化,然而整体形状却具有相似性。碎石颗粒的破碎过程可以用Koch曲线形象的描述。在这个过程中产生的小石块同原来的大石块相似,因此填料的破碎具有分形特征。
2 粒径分布函数的分形表示
对于填石路基填料,设其填料的颗粒直径为δ,定义粒径不大于δ的填料个数为N(δ),可得到分形为:

其中,δmax为填料的最大粒径;NZ为填料的总数目。
填料的粒径分布函数F(δ)定义为:

则:
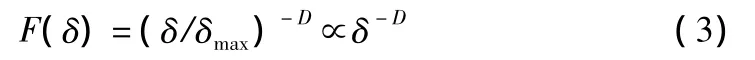
其分维数D可以表征颗粒的相对粗细,D值越大,说明小于给定直径大小的颗粒越多,对应颗粒整体越细[3]。
3 填石料的分形
填料粒径分布为分形,则其相应的质量、孔隙率、毛体积等也是空间意义上的分形。其拓扑维数为3,因此根据分形的定义可以得到毛体积的分形表达式为:
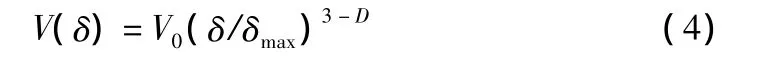
其中,V(δ)为粒径不大于δ的填料颗粒的毛体积;V0为所有填料的毛体积。
对上式求导:
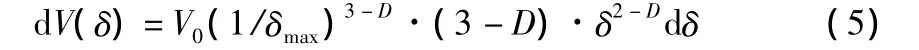
定义粒径小于δ填料的质量M(δ),则有:
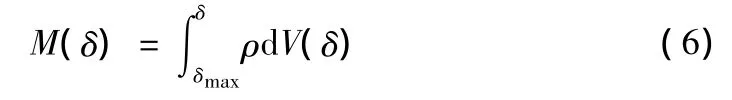
由式(5),式(6)得:
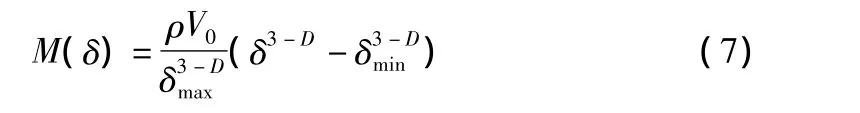
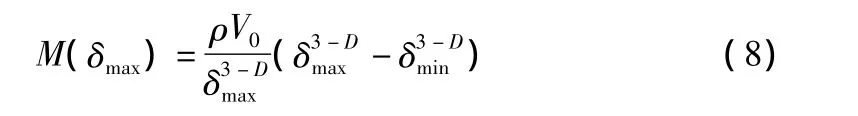
其中,M(δ)为粒径不大于δ的填料的质量;ρ为填料的表观密度。
定义填料的质量分布函数:

其中,P(δ)为筛孔为δ的质量通过百分率;MZ为填料的总质量,即 M(δmax)。
由式(7)和式(8)可得:
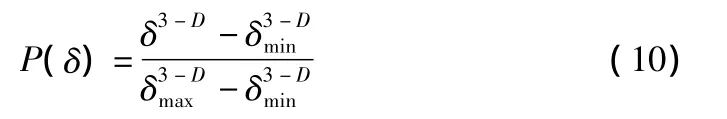
当 δ=δmax时:
当最小的粒径δmin=0时,下式成立:

此即为质量通过率表示的填料级配分形表达式。
对式(11)取对数得:
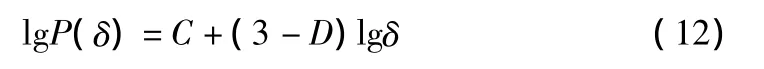
如果在双对数坐标lgP与lgδ函数图中存在直线段,就表明填料颗粒分布具有分形结构,lgP与lgδ的关系用数学方法回归是一次方程,故lgP与lgδ存在直线关系,利用EXCEL中的最小二乘法对已知数据进行最佳直线拟合,求出通过百分率lgP与孔尺寸lgδ之间的最佳拟合直线斜率为K,则D=3-K,不同的D值对应不同的级配组成[4]。
4 分形维数和碎石料级配的关系
分维数的大小与粒径级配曲线的特征值有关,也与lg[M(d)/M]-lgδ曲线斜率有关。该曲线斜率b越大,分维数D越小[5]。
根据不均匀系数Cu=d60/d10和曲率系数可推算得分维数D与不均匀系数Cu和曲率系数Cc的以下关系式:

根据土工试验规程,当粗粒土的级配同时满足:Cu≥5和Cc=1~3时为级配良好。由JTG F10-2006公路路基施工技术规范,不均匀系数范围限定在10~15之间,由式(13)和式(14)计算出当D满足1.887~2.631范围时,颗粒级配良好。因此,当填料的粒度分布分维数满足D在以上范围时,其级配为良好级配。只需计算分维值,就可以判定级配优良性。根据分维数与不均匀系数和曲率的关系可以知道,D值越大,颗粒大小越不均匀,工程性质越好;D值越小,颗粒大小均匀,工程性质越差。
5 试验结果分析
由室内填料筛分试验,得出三种试样通过各筛孔的质量占总质量的百分比。筛下累计百分含量如表1所示。
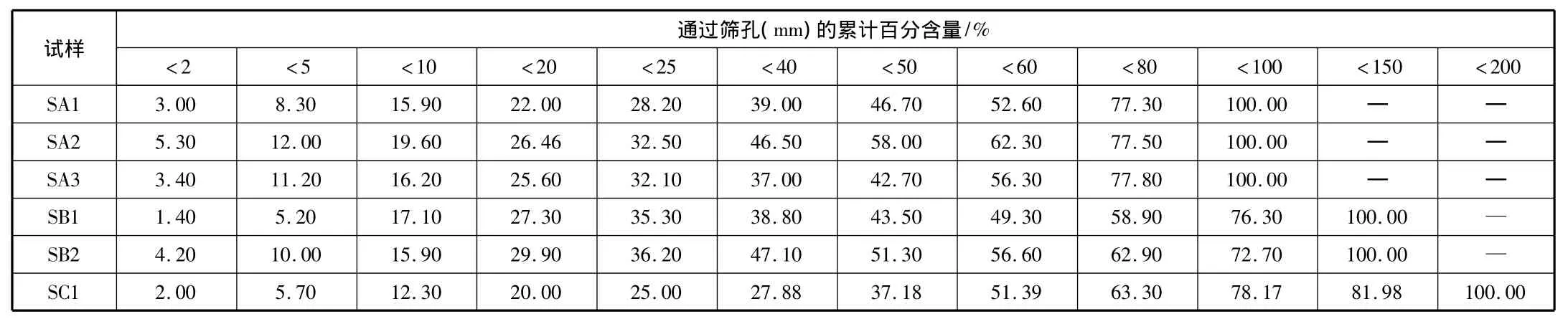
表1 碎石筛下百分含量
假定:
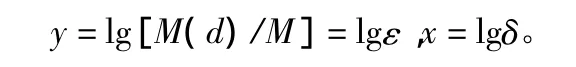
则可作出三种填料SA,SB,SC的分形结构图如图1~图3所示。
对所做曲线经过线性拟合得到直线段,直线的斜率即为b。SA料的斜率 b=0.775 8,SB料的斜率 b=0.816 1,SC料的斜率b=0.837 9。根据分维数与斜率的关系D=3-K得出三种填料的分维数分别如表2所示。
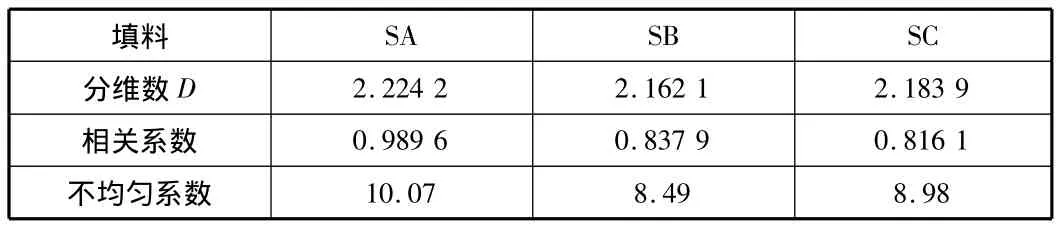
表2 分维数计算
从图1~图3各组填料的分维结构、表1的数据分析可以看出分维数D全部满足1.887~2.631的范围,SA的填料分维数值最大,数值拟合计算得到的分维值与筛分试验所得的不均匀系数这两个指标有很好的统一性及不均匀性,不均匀系数越大,分维值就越大,填料粒径分布越好。在拟合分维值时,除了SB组填料外,相关系数都在0.98以上,说明变量之间的线性相关程度很高及拟合结果有很高的可信度。
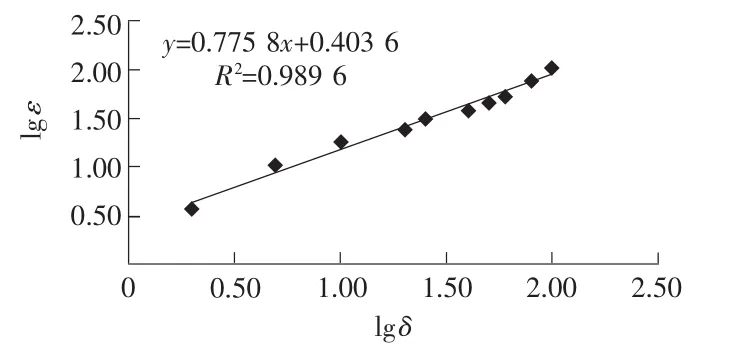
图1 SA填料分维数结构图
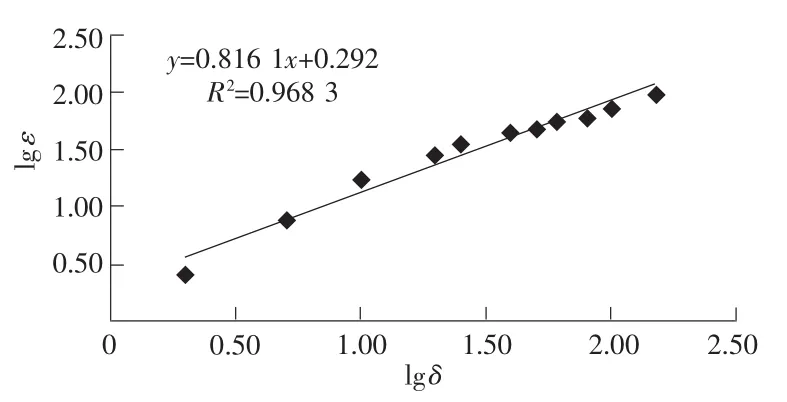
图2 SB填料分维数结构图
由图4可以看出,填料SA的粒径分布曲线比SB,SC组填料更要光滑,曲线相对平缓,没有太大的波动点和突变点,可知分维值最大的SA组填料中小粒径颗粒最多,粒径分布不均匀。所以可以利用分维数的大小范围来表征碎石填料级配的粗细及其粒径分布特征。
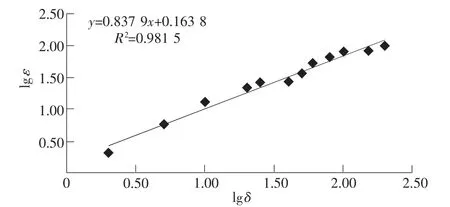
图3 SC填料分维数结构图
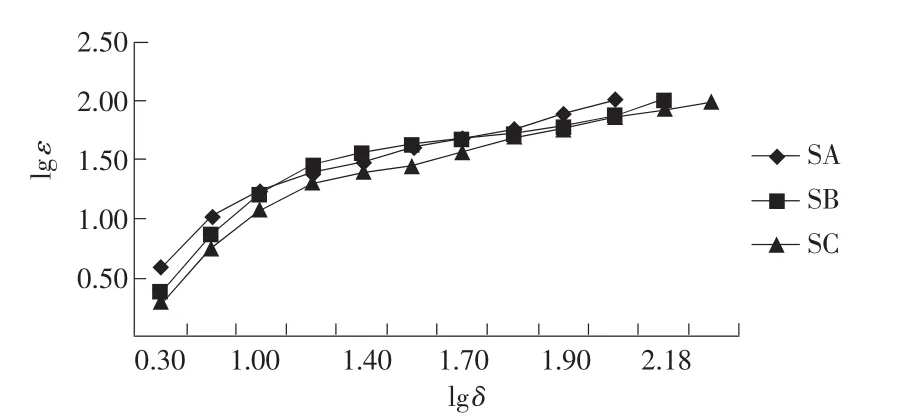
图4 各组填料粒径分布曲线图
6 结语
1)碎石填料的粒径分布特点具有良好的分形结构,利用分形维数可以评价填料级配组成的优劣。当分形维数的值在1.887~2.631之间时,可以判断为良好级配;
2)分维数越大,填料粒径分布曲线越平缓,填料级配良好;
3)细颗粒成分越多,分维数越大;粗颗粒成分越多,分维数越小。用分维数可以定量描述填石料中各种粗细颗粒的含量。
[1]褚武扬.材料科学中的分形[M].北京:化学工业出版社,2004:167-186.
[2]张济忠.分形[M].北京:清华大学出版社,1995.
[3]薛祥立.粒度分布函数的分形表示[J].青岛建筑工程学院学报,1997,18(14):81-82.
[4]李国强.矿料级配的分形特征研究[J].重庆交通学院学报,1995,14(2):129-130.
[5]付玉珠.填石路基大粒径填料特性试验研究[D].成都:西南交通大学,2013.
