基于货币时间价值表的时间轴运用研究

安阳师范学院 陈 艳

货币时间价值是指货币随着时间的推移而产生的价值增值，时间越长，增值越多。货币时间价值的表现形式有多种：如果是一次性投入的款项，按照计息方式，有单利和复利之分，其中单利只对本金计息，而复利对本金所产生的利息也要计息；如果是定期等额收付款项，就是年金，按照收付的时间点，可进一步分为普通年金、预付年金、递延年金和永续年金，其中普通年金是指从第一年开始，每年年末等额收付的年金形式，而预付年金则是从第一年开始，每年年初等额收付的年金，递延年金的第一次收付点不是第一年，永续年金没有到期日。在多种货币时间价值的表现形式中，单利比复利的运算简单，应用较少，而年金中，普通年金是其它年金的基础，所以，货币时间价值的研究重点在复利和普通年金上。

为了辅助货币时间价值的计算，就出现了货币时间价值表。货币时间价值表一般有四个，即一元复利终值表、一元复利现值表、一元年金终值表和一元年金现值表。其中，终值是指现在一定量的资金在未来某一时点上的价值，而现值是指对未来的现金收付按照一定的折现率进行折现后的现在价值。现笔者以10%的折现率为例列出其在若干期的四个系数表的相关数据。

表1 折现率i=10%时的货币时间价值表

初学货币时间价值，往往先要接触这样的货币时间价值表。对于这个表的查法，经过简单的学习，一般都能快速地掌握。可是，对于表中各个数据的含义以及数据间的内在联系，往往缺乏研究，也很难掌握。如果能够通过一定的方法简单快速地掌握货币时间价值表中的数据，对于货币时间价值的深入了解和灵活运用将会有很大的帮助。

一、货币时间价值表中时间轴的运用

时间轴是研究货币时间价值的必要手段和辅助工具。图1是一个简单的时间轴，在此轴中，起点0表示第一年年初，终点n表示第n年年末，除此两点之外，其他的时间点都有两个含义，既表示该年年末，又表示下年年初。如，时间点1即是第一年年末，又是第二年年初。

图1 时间轴

运用时间轴，能够将货币时间价值表中的数据表示在这条轴上。下面把表1中折现率为10%，期数为第10期的四个数据分别表示在相应的时间轴中。

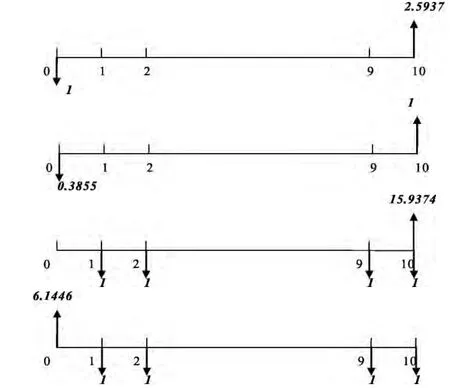
图2 折现率为10%，期数为10期的时间轴

以上四条时间轴中，第一条时间轴是当折现率i=10%，期数n=10时的复利终值系数，其中2.5937的含义是指“如果在第一年年初投入1元钱，在年复利率为10%，每年复利一次的情况下，到第十年年末的本利和就是2.5937元”。

第二条时间轴是当折现率i=10%，期数n=10时的复利现值系数，其中0.3855的含义是指“如果想十年后的本利和达到1元钱，在年复利率为10%，每年复利一次的情况下，第一年年初要投入0.3855元”。

第三条时间轴是当折现率i=10%，期数n=10时的年金终值系数，其中15.9374的含义是指“如果从第一年开始，每年年末投入1元钱，共投入十年，在年复利率为10%，每年复利一次的情况下，到第十年年末的本利和就是15.9374元”。

第四条时间轴是当折现率i=10%，期数n=10时的年金现值系数，其中6.1446的含义是指“如果从第一年开始，每年年末投入1元钱，共投入十年，在年复利率为10%，每年复利一次的情况下，折现到第一年年初就是6.1446元”。

通过时间轴，了解了货币时间价值表中每个数据的含义，下一步就要研究这些数据之间的内在联系了。

二、货币时间价值表中各数据的关系

（一）复利终值与现值的关系 从图2中前两条时间轴上可以看出，第一年年初的1元钱到第十年年末就成了2.5937元，那么，如果十年后要有1元钱，第一年年初就要投入1/2.5937元，而这个结果正好就是0.3855元。所以说，复利终值与现值互为倒数关系。

（二）年金终值与现值的关系 在图2的后两条时间轴上，从第一年开始，每年年末投入1元钱，共十年，折算到第十年年末就是15.9374元，而折现到第一年年初则是6.1446元。这里的15.9374和6.1446的关系其实就是分别互为终值和现值，即：15.9374×（P/F,10%,10）=15.9374×0.3855≈6.1446；6.1446×（F/P,10%,10）=6.1446×2.5937≈15.9374。

（三）复利与年金的关系（1）复利终值与年金终值的关系。图2中第三条时间轴是10年期的年金终值系数，从图中可看出它等于从第1点到第10点各点投入1元钱的复利终值之和，而在第一条复利终值时间轴中，10年期的复利终值系数的资金投入点是在0点。这就说明，年金终值系数应该是从9年期到8年期，一直到0年期各期复利终值系数之和，即15.9374=2.3579+2.1436+1.9487+1.7716+1.6105+1.4641+1.3310+1.2100+1.1000+1。

（2）复利现值与年金现值的关系。图2中第四条时间轴是10年期的年金现值系数，从图中可看出它等于从第1点到第10点各点投入1元钱的复利现值之和，而在第二条复利现值时间轴中，10年期的复利现值系数的1元钱所在的点是在第10点。这就说明，年金现值系数应该是从10年期到9年期，一直到1年期各期复利现值系数之和，即6.1446=0.3855+0.4241+0.4665+0.5132+0.5645+0.6209+0.6830+0.7513+0.8264+0.9091。

（四）普通年金与预付年金的关系 预付年金是指发生在每期期初的等额收付款项，相对于发生在每期期末的等额收付款项普通年金而言，无论是终值还是现值，都是多计了一期的利息。所以预付年金终值=（F/A，i，n）×（1+i），预付年金现值=（P/A，i，n）×（1+i）。如果查年金系数表的话，预付年金终值系数应该在普通年金终值的基础上，期数加1，整体系数再减1得到；而预付年金现值系数应该在普通年金现值的基础上，期数减1，整体系数再加1得到。比如说，要得到折现率为10%，期数为10期的预付年金终值，要先查期数为11期的年金终值系数，找到18.5312，再减去1得到17.5312；要得到折现率为10%，期数为10期的预付年金现值，要先查期数为9期的年金现值系数，找到5.7590，再加上1得到6.7590。

三、以时间轴反映数据之间的关系

（一）正负时间轴的运用——反映互为倒数关系的数据 对于时间轴，常见的都是正的时间轴，下面笔者引入一种负的时间轴，如下图3所示。

图3 负时间轴

在图3中，起点-n表示前n年的年末，终点0表示去年的年末，同时也是今年的年初，也就是现在所处的时间点，其他的时间点都有两个含义，一是表示前1年的年末，二是表示该年的年初。比如说，时间点1即是前年的年末，又是去年的年初。

通过负时间轴和正时间轴的结合形成的综合时间轴，就能够在一条轴上同时反映出互为倒数关系的数据。在货币时间价值体系中，互为倒数关系的数据一共有三对，除了前文提到的复利终值和复利现值互为倒数外，年金终值系数与年偿债基金系数、年金现值系数与年资本回收系数也互为倒数关系。下面笔者还是以折现率为10%，期数为10期的情况，列出三条正负时间轴来表示三组互为倒数的数据，如下图4、5、6所示。

图4 折现率为10%时的复利现值系数和复利终值系数

图4中，如果前十年年末投入0.3855元，在年复利率为10%的情况下，到今年年初，本利和就达到了1元钱；今年年初的1元钱，在年复利率为10%的情况下，到第10年年末，本利和就是2.5937元。其中的0.3855和2.5937分别是复利现值系数和复利终值系数，两者互为倒数。

图5 折现率为10%时的年偿债基金系数和年金终值系数

图5中，如果从前10年的年初开始，每年年初投入1/15.9374元，连续10年，一直到今年年初，在年复利率为10%的情况下，到今年年初，本利和为1元钱；从今年年末开始，每年年末投入1元钱，连续10年，一直到第10年年末，在年复利率为10%的情况下，到第10年年末的本利和为15.9374元。其中的1/15.9374和15.9374分别是年偿债基金系数和年金终值系数，两者互为倒数。

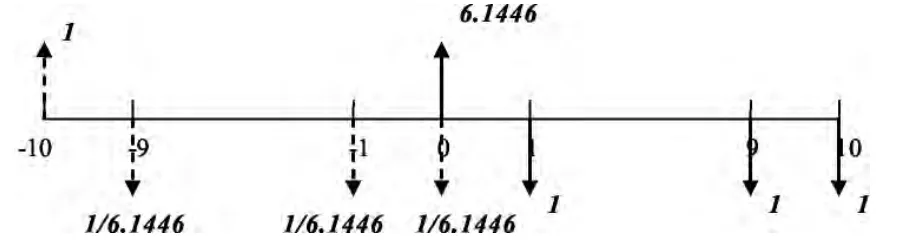
图6 折现率为10%时的年资本回收系数和年金现值系数

图6中，如果从前10年的年初开始，每年年初投入1/6.1446元，连续10年，一直到今年年初，在年复利率为10%的情况下，折现到前10年年末，就是1元；从今年年末开始，每年年末投入1元钱，连续10年，一直到第10年年末，在年复利率为10%的情况下，折现到今年年初就是6.1446元。其中的1/6.1446和6.1446分别是年资本回收系数和年金现值系数，两者互为倒数。

通过以上3个正负时间轴，就把三种互为倒数关系的数据以及他们之间的换算关系完整地反映在一起了。

（二）综合时间轴的运用——反映互为现值和终值关系的数据 货币时间价值体系中，互为现值和终值关系的数据有两对：普通年金现值与终值、预付年金现值与终值。可以在一条时间轴上反映出两者的关系来，如下图7、8所示。

图7 普通年金现值系数与终值系数

图7中，从第1年开始，每年年末投入1元钱，连续10年，在年复利率为10%的情况下，到第10年年末，本利和达到15.9374元；如果折现到第1年年初的话，则是6.1446元。从时间轴上可以看出，15.9374在第10点，6.1446在0点，两者刚好就是终值和现值的关系。

图8 预付年金现值系数与终值系数

图8中，从第1年开始，每年年初投入1元钱，连续10年，在年复利率为10%的情况下，到第10年年末，本利和达到17.5312元；如果折现到第1年年初的话，则是6.7590元。从时间轴上可以看出，17.5312在第10点，6.7590在0点，两者也是终值和现值的关系。

（三）综合时间轴的运用——反映普通年金与预付年金的关系 无论是预付年金终值还是现值，都是在普通年金终值和现值的基础上多计了1期利息，同样也可以在同一条时间轴上反映出这个联系，如下图9、10所示。

图9 普通年金终值系数与预付年金终值系数

在图9中，10个1元钱的资金投入点是一样的，都是从1到10十个点，折现率也一样，都是10%，但是，由于代表的含义不一样，就会在不同的点产生不同的终值。如果把这十个点看作是每年年末，亦即从第1年年末开始，一直到第10年末为止，这就是普通年金，到第10年年末，普通年金的终值就是在第10点的15.9374元；如果把这十个点看作是每年年初，亦即从第2年年初开始，一直到第11年初为止，这就是预付年金，到第11年年末，预付年金的终值就是在第11点的17.5312元。从时间轴上看，15.9374与17.5312刚好相差一期，两者的关系是15.9374×（1+10%）=17.5312。

图10 普通年金现值系数与预付年金现值系数

在图10中，10个1元钱的资金投入点是一样的，都是从1到10十个点，折现率也一样，都是10%，但也是由于代表的含义不一样，就会在不同的点产生不同的现值。如果把这十个点看作是每年年末，亦即从第1年年末开始，一直到第10年末为止，这就是普通年金，折现到第1年年初，普通年金的现值就是在第0点的6.1446元；如果把这十个点看作是每年年初，亦即从第2年年初开始，一直到第11年初为止，这就是预付年金，折现到第2年年初，预付年金的现值就是在第1点的6.7590元。从时间轴上看，6.1446与6.7590刚好相差一期，两者的关系是6.1446×（1+10%）=6.7590。

通过以上的分析，如果能够巧妙运用时间轴，就能够把复杂的货币时间价值表中的数据以及数据之间的关系体现在一条条简单的线段上，达到化繁为简的效果。

［1］毛付根：《管理会计》，高等教育出版社2007年版。